本文主要是介绍【论文阅读】DMGI:Unsupervised Attributed Multiplex Network Embedding,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
无监督属性化多路复用网络嵌入
- 摘要
- 1 引言
- 2 问题陈述
- 3 Unsupervised Attributed Multiplex Network Embedding
- 3.1 Deep Multiplex Graph Infomax: DMGI
- 4 实验
摘要
多路复用网络中的节点由多种类型的关系连接。然而,大多数现有的网络嵌入方法都假设节点之间只存在一种单一的关系。即使对于考虑网络多重性的人,他们也会忽略节点属性,使用节点标签进行训练,并且无法对图的全局属性建模。受DGI最大化局部patches和整个图的全局表示之间的互信息的启发,我们提出了一种无监督网络嵌入方法DMGI。我们设计了一个系统的方法来联合集成多个图的节点嵌入,方法是:1)引入一致性正则化框架,最大限度地减少特定关系类型的节点嵌入之间的分歧;2)不管关系类型如何,都能区分真实样本的通用鉴别器。我们还表明,注意力机制推断了每种关系类型的重要性,因此可以作为预处理步骤用于过滤不必要的关系类型。对各种下游任务的大量实验表明,尽管DMGI是完全无监督的,但DMGI优于最先进的方法。
1 引言
- 其他多路复用网络嵌入的问题:
(1)专注于多个图的集成,但忽略了节点属性。
(2)考虑到了节点属性,但训练时需要节点标签。
(3)不能建模图的全局特性(因为它们都基于基于随机游走的skip-gram模型或GCN,这两者都可有效捕获局部图结构)。
- DGI的优点:
(1)通过GCN自然地集成节点属性。
(2)以无监督方式训练。
(3)可以捕获整个图的全局结构。
2 问题陈述
- 定义:属性化多路复用网络(Attributed Multiplex Network)
G = { G 1 , G 2 , . . . , G ∣ R ∣ } = { V , E , X } \mathcal{G}=\{\mathcal{G}^1,\mathcal{G}^2,...,\mathcal{G}^{\mathcal{|R|}}\}=\{\mathcal{V},\mathcal{E},\pmb{X}\} G={G1,G2,...,G∣R∣}={V,E,XXX} 。
其中, G r = { V , E ( r ) , X } \mathcal{G}^r=\{\mathcal{V},\mathcal{E}^{(r)},\pmb{X}\} Gr={V,E(r),XXX}是关系类型 r ∈ R r∈\mathcal{R} r∈R的图, V \mathcal{V} V是 n n n个节点的集合, E = ⋃ r ∈ R E ( r ) ⊆ V × V \mathcal{E}=\bigcup_{r∈\mathcal{R}}\mathcal{E}^{(r)}\subseteq\mathcal{V}×\mathcal{V} E=⋃r∈RE(r)⊆V×V是关系类型为 r ∈ R r∈\mathcal{R} r∈R的所有边的集合, X ∈ R n × f \pmb{X}∈\mathbb{R}^{n×f} XXX∈Rn×f是编码 n n n个节点属性信息的矩阵。
对于多路复用网络, ∣ R ∣ > 1 \mathcal{|R|}>1 ∣R∣>1;对于单个网络, ∣ R ∣ = 1 \mathcal{|R|}=1 ∣R∣=1。
给定网络 G \mathcal{G} G, A = { A ( 1 ) , . . . , A ( ∣ R ∣ ) } \mathcal{A}=\{\pmb{A}^{(1)},...,\pmb{A}^{(|R|)}\} A={AAA(1),...,AAA(∣R∣)}是一组邻接矩阵,其中 A ( r ) ∈ { 0 , 1 } ∣ V ∣ × ∣ V ∣ \pmb{A}^{(r)}∈\{0,1\}^{|V|×|V|} AAA(r)∈{0,1}∣V∣×∣V∣是网络 G r \mathcal{G}^r Gr的邻接矩阵。
- 任务:无监督属性化多路复用网络嵌入(Unsupervised Attributed Multiplex Network Embedding)
给定一个属性化多路复用网络 G = { V , E , X } \mathcal{G}=\{\mathcal{V},\mathcal{E},\pmb{X}\} G={V,E,XXX}以及邻接矩阵的集合 A \mathcal{A} A,任务是在不使用任何标签的情况下,学习每个节点 v i ∈ V v_i∈\mathcal{V} vi∈V的 d d d维向量表示 z i ∈ Z ∈ R n × d \pmb{z}_i∈\pmb{Z}∈\mathbb{R}^{n×d} zzzi∈ZZZ∈Rn×d。
3 Unsupervised Attributed Multiplex Network Embedding
3.1 Deep Multiplex Graph Infomax: DMGI
我们首先描述如何独立地建模每个关系类型相关的图,然后解释如何联合集成它们,最终得到一致性节点嵌入矩阵。
(1)特定关系类型的节点嵌入
对于每个关系类型 r ∈ R r∈\mathcal{R} r∈R,我们引入一个特定关系类型的节点嵌入编码器 g r = R n × f × R n × n → R n × d g_r=\mathbb{R}^{n×f}×\mathbb{R}^{n×n}→\mathbb{R}^{n×d} gr=Rn×f×Rn×n→Rn×d来生成 G ( r ) \mathcal{G}^{(r)} G(r)中节点的特定关系类型的节点嵌入矩阵 H ( r ) \pmb{H}^{(r)} HHH(r)。该编码器是一个单层的GCN:
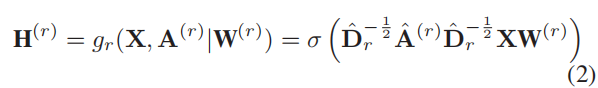
其中,
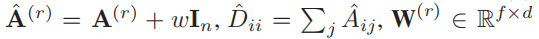
W ( r ) \pmb{W}^{(r)} WWW(r)是特定关系类型编码器 g r g_r gr的可训练矩阵, σ \sigma σ是ReLU非线性函数。
与传统的GCN不同,我们通过引入权重 w ∈ R w∈\mathbb{R} w∈R来控制自连接的权重。较大的 w w w表明,节点本身在生成其嵌入中起着更重要的作用,这反过来又降低了其相邻节点的重要性。
然后,我们计算了总结图 G ( r ) \mathcal{G}^{(r)} G(r)的全局内容的图级summary representation s ( r ) \pmb{s}^{(r)} sss(r)。我们使用一个Readout函数: R n × d → R d \mathbb{R}^{n×d}→\mathbb{R}^d Rn×d→Rd:
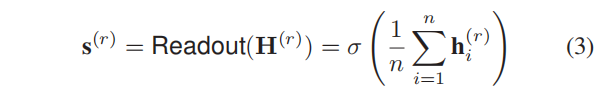
其中, σ \sigma σ是sigmoid函数, h i ( r ) h^{(r)}_i hi(r)表示矩阵 H ( r ) \pmb{H}^{(r)} HHH(r)的第 i i i行向量。我们还注意到,各种池化方法,如maxpool和SAGPool都可用作Readout(·)。
接下来,给定特定关系类型的节点嵌入矩阵 H ( r ) \pmb{H}^{(r)} HHH(r)及其summary representation s ( r ) \pmb{s}^{(r)} sss(r),我们计算了特定关系类型的交叉熵:
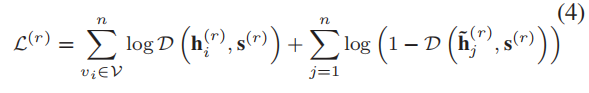
其中, D ∈ R d × R d → R \mathcal{D}∈\mathbb{R}^d×\mathbb{R}^d→\mathbb{R} D∈Rd×Rd→R是一个计算patch-summary表示对(即 ( h i ( r ) , s ( r ) ) (\pmb{h}_i^{(r)},\pmb{s}^{(r)}) (hhhi(r),sss(r)))分数的discriminator。在本文中,我们应用了一个简单的双线性评分函数,因为它在我们的实验中表现最好:
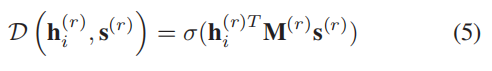
其中, σ \sigma σ是sigmoid函数, M ( r ) ∈ R d × d \pmb{M}^{(r)}∈\mathbb{R}^{d×d} MMM(r)∈Rd×d是一个可训练的评分矩阵。
为了生成负节点嵌入 h ~ j ( r ) \widetilde{h}_j^{(r)} h j(r),我们通过逐行变换来破坏原始属性矩阵【只变换了节点的属性,故 A ( r ) 、 W ( r ) \pmb{A}^{(r)}、\pmb{W}^{(r)} AAA(r)、WWW(r)没变】,即 X ~ ← X \widetilde{\pmb{X}}←\pmb{X} XXX ←XXX,并重复使用公式(2)中的编码器,即 H ~ ( r ) = g r ( X ~ , A ( r ) ∣ W ( r ) ) \widetilde{\pmb{H}}^{(r)}=g_r(\widetilde{\pmb{X}},\pmb{A}^{(r)}|\pmb{W}^{(r)}) HHH (r)=gr(XXX ,AAA(r)∣WWW(r))。
(2)联合建模与一致性正则化
在此之前,通过独立地最大化与每个图 G ( r ) \mathcal{G}^{(r)} G(r)( ∀ r ∈ R \forall r∈\mathcal{R} ∀r∈R)相关的局部patches { h 1 ( r ) , h 2 ( r ) , . . . , h n ( r ) } \{\pmb{h}^{(r)}_1,\pmb{h}^{(r)}_2,...,\pmb{h}^{(r)}_n\} {hhh1(r),hhh2(r),...,hhhn(r)}和图级summary s ( r ) \pmb{s}^{(r)} sss(r)之间的平均MI,我们获得了特定关系类型的节点嵌入矩阵 H ( r ) \pmb{H}^{(r)} HHH(r),它在 G ( r ) \mathcal{G}^{(r)} G(r)中捕获全局信息。
然而,由于每个 H ( r ) \pmb{H}^{(r)} HHH(r)都是为每个 r ∈ R r∈\mathcal{R} r∈R独立训练的,这些嵌入矩阵只包含关于每种关系类型的相关信息,因此无法利用网络的多重性。这促使我们开发一种系统的方法来联合集成来自不同关系类型的嵌入,以便促进它们相互帮助彼此学习高质量的嵌入。
为此,我们引入了一致性嵌入矩阵 Z ∈ R n × d \pmb{Z}∈\mathbb{R}^{n×d} ZZZ∈Rn×d,每个特定关系类型的节点嵌入矩阵 H ( r ) \pmb{H}^{(r)} HHH(r)都可以在其上一致。更准确地说,我们引入了一致性正则化框架,该框架包括:
- 一个正则化器,用来最小化原始节点嵌入 { H ( r ) ∣ r ∈ R } \{\pmb{H}^{(r)}|r∈\mathcal{R}\} {HHH(r)∣r∈R}与一致性嵌入 Z \pmb{Z} ZZZ间的差异。
- 另一个正则化器,用来最大化 corrupted 节点嵌入 { H ~ ( r ) ∣ r ∈ R } \{\widetilde{\pmb{H}}^{(r)}|r∈\mathcal{R}\} {HHH (r)∣r∈R}与与一致性嵌入 Z \pmb{Z} ZZZ间的差异。
其表述如下:
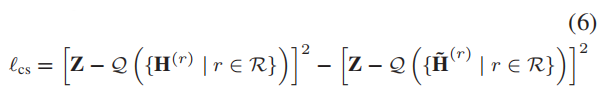
其中, Q \mathcal{Q} Q是一个聚合函数,它将一组来自多个关系类型的节点嵌入矩阵组合到一个嵌入矩阵中,即 H ∈ R n × d \pmb{H}∈\mathbb{R}^{n×d} HHH∈Rn×d。 Q \mathcal{Q} Q可以是任何可以处理序列不变量输入的池化方法,如 set2set 或 Set Transformer。然而,考虑到该方法的有效性,我们只是简单地使用平均池化,即计算嵌入矩阵集的平均值:
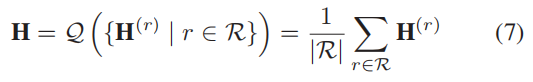
需要注意的是,公式(5)中的评分矩阵 M ( ∗ ) \pmb{M}(∗) MMM(∗)在所有的关系 r ∈ R r∈\mathcal{R} r∈R中共享。即 M = M ( 1 ) = M ( 2 ) = . . . = M ( ∣ R ∣ ) \pmb{M}=\pmb{M}^{(1)}=\pmb{M}^{(2)}=...=\pmb{M}^{(|R|)} MMM=MMM(1)=MMM(2)=...=MMM(∣R∣)。直觉是学习通用discriminator,它能够在不考虑关系类型的情况下,对真实对的评分高于负对。我们认为,通用discriminator促进了不同关系类型的联合建模以及一致性正则化。
最后,我们联合优化了公式(4)中所有特定关系类型损失的总和,以及公式(6)中的一致性正则化,获得最终目标 J \mathcal{J} J,如下所示:
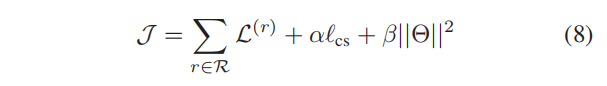
其中 α α α控制了一致性正则化的重要性, β β β是 Θ Θ Θ上 l 2 l2 l2正则化项的系数, Θ Θ Θ是一组可训练的参数,即 Θ = { { W ( r ) ∣ r ∈ R } 、 M 、 Z } Θ=\{\{\pmb{W}^{(r)}|r∈\mathcal{R}\}、\pmb{M}、\pmb{Z}\} Θ={{WWW(r)∣r∈R}、MMM、ZZZ}, J \mathcal{J} J由Adam优化器进行优化。
图1说明了DMGI的概述。

(3)讨论
尽管效率很高,但公式(7)中平均池化方案平等地对待所有关系,然而,如实验所示,某些关系类型比其他类型更适合某个下游任务。
例如,与引文信息相比,两篇论文之间的合著信息在预测论文主题方面起着更重要的作用;最终,这两种信息相互帮助,可以更准确地预测论文的主题。
因此,我们可以采用注意力机制来区分不同的关系类型,如下所示:
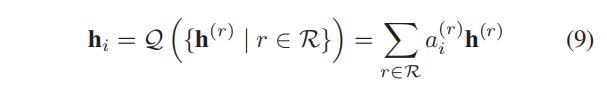
其中, a i ( r ) a^{(r)}_i ai(r)表示关系 r r r在生成节点 v i v_i vi的最终嵌入时的重要性,其定义为:
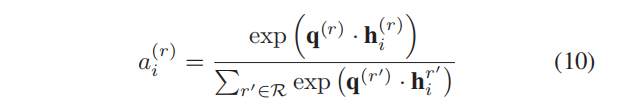
其中, q ( r ) ∈ R d \pmb{q}^{(r)}∈\mathbb{R}^d qqq(r)∈Rd是关系 r r r的特征向量。
(4)扩展到半监督学习
值得注意的是,DMGI是以一种完全无监督的方式进行训练的。然而,在实际上,节点有时与标签信息相关联,即使有少量的信息,这也可以指导节点嵌入的训练。为此,我们在我们的框架中引入了一个半监督模块,它从一致性嵌入 Z \pmb{Z} ZZZ中预测标记节点的标签。更准确地说,我们最小化了标记节点上的交叉熵误差:
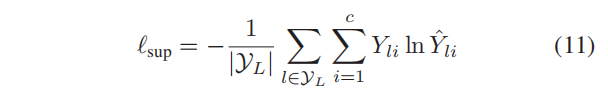
其中, Y L \mathcal{Y}_L YL是带有标签的节点索引集, Y ∈ R n × c Y∈\mathbb{R}^{n×c} Y∈Rn×c是ground truth标签, Y ^ = s o f t m a x ( f ( Z ) ) \hat{Y}=softmax(f(\pmb{Z})) Y^=softmax(f(ZZZ))是一个softmax层的输出, f : R n × d → R n × c f:\mathbb{R}^{n×d}→\mathbb{R}^{n×c} f:Rn×d→Rn×c是一个分类器,它从嵌入预测节点的标签,是一个单个的全连接层。
具有半监督模块的最终目标函数是:
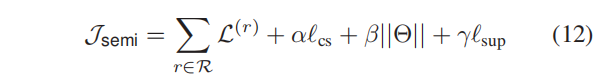
4 实验



这篇关于【论文阅读】DMGI:Unsupervised Attributed Multiplex Network Embedding的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!









