牛客周赛 Round 36 解题报告 | 珂学家 | 状态DP + 构造 + 9棵树状数组

题型: 签到

s = input()print (s[:-3])

思路: 模拟

h, w, s = list(map(int, input().split()))ts = 0
grid = []
for i in range(h):arr = list(map(int, input().split()))grid.append(arr)ts += sum(arr) hs = set()
for i in range(h):v = 0for u in grid[i]:v = v ^ uhs.add(v)
for i in range(w):v = 0for j in range(h):v ^= grid[j][i]hs.add(v)if len(hs) == 1 and ts == s:print ("accepted")
else:print ("wrong answer")

思路: 状态机DP

引入三个状态

• 0, 末尾是空格，
• 1, 末尾是小写字母
• 2, 末尾是大写字母

具体转移和当前的字母的大小写性质有关

具体看代码

s = input()from math import infdp0, dp1, dp2 = 0, inf, infn = len(s)
for c in s:if c >= 'A' and c <= 'Z':t0 = min(dp0, dp1, dp2) + 1t1 = inft2 = dp0dp0, dp1, dp2 = t0, t1, t2else:t0 = min(dp0, dp1, dp2) + 1t1 = min(dp0, dp1, dp2)t2 = infdp0, dp1, dp2 = t0, t1, t2print (min(dp0, dp1, dp2))

思路: BFS

很板的一道题，只是在扩展下一步的时候，多了一个限制条件

h, w = list(map(int, input().split()))maze = []
for _ in range(h):arr = list(input())maze.append(arr)from math import inf
from collections import dequevis = [[inf] * w for _ in range(h)]deq = deque()
deq.append((0, 0))
vis[0][0] = 0while len(deq) > 0:y, x = deq.popleft()for (dy, dx) in [(-1, 0), (1, 0), (0, -1), (0, 1)]:ty = y + dytx = x + dxif 0 <= ty < h and 0 <= tx < w:if maze[y][x] != maze[ty][tx]:if vis[ty][tx] > vis[y][x] + 1:vis[ty][tx] = vis[y][x] + 1deq.append((ty, tx))if vis[h - 1][w - 1] == inf:print (-1)
else:print (vis[h - 1][w - 1])

思路: 构造一个弯

按照Case 1，构造一个”钩“，然后其余的保持和周边不同即可。

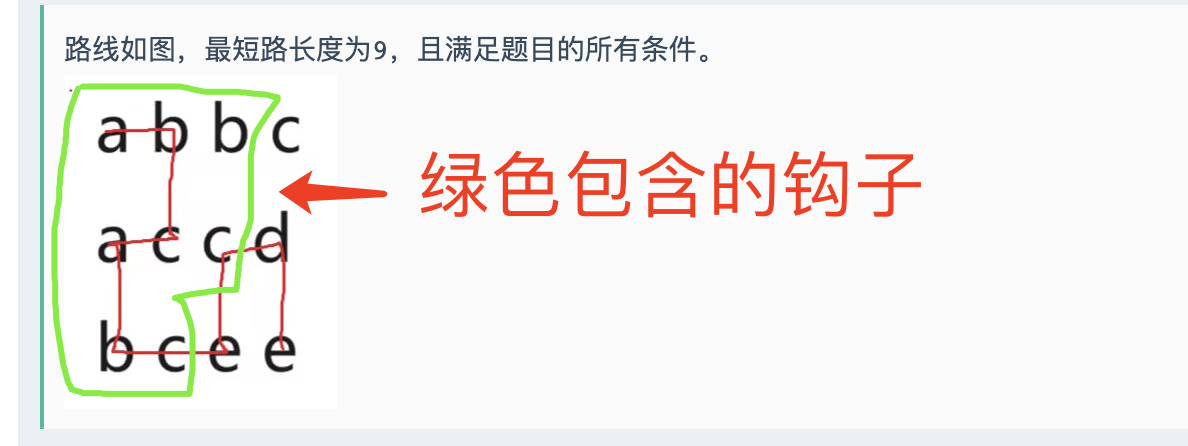
因为地图四色定律，所以只要”abcd“即可。

h, w = list(map(int, input().split()))maze = [['A'] * w for _ in range(h)]
maze[0][0] = 'a'
maze[0][1] = 'b'
maze[0][2] = 'b'maze[1][0] = 'a'
maze[1][1] = 'c'
maze[1][2] = 'c'maze[2][0] = 'b'
maze[2][1] = 'c'def compute(y, x):s = set()for (dy, dx) in [(-1, 0), (1, 0), (0, -1), (0, 1)]:ty, tx = y + dy, x + dxif 0 <= ty < h and 0 <= tx < w:if maze[ty][tx] != 'A':s.add(maze[ty][tx])for c in "abcd":if c not in s:return creturn 'e'for i in range(h):for j in range(w):if maze[i][j] == 'A':maze[i][j] = compute(i, j)for i in range(h):print (''.join(maze[i]))

思路: 经典结论 + 树状数组

不存在 大于等于2个子串的回文，

$$red的排列p，然后p循环出现$$

基于这个结论，对于某个查询[l, r], 则枚举red的排列，然后引入9个树状数组, 进行统计，求最小代价即可。

fenwicks[3][3]，表示位置余3，字母(按red=123）的9个树状数组

class BIT(object):def __init__(self, n):self.n = nself.arr = [0] * (n + 1)def query(self, p):r = 0while p > 0:r += self.arr[p]p -= p & -preturn rdef update(self, p, d):while p <= self.n:self.arr[p] += dp += p & -pdef toId(ch):if ch == 'r':return 0elif ch == 'e':return 1return 2from math import inf
from itertools import permutations n, m = list(map(int, input().split()))
s = list(input())trees = [ [ BIT(n) for _ in range(3) ] for _ in range(3)]for i in range(n):trees[i % 3][toId(s[i])].update(i + 1, 1)for _ in range(m):op, a1, a2 = input().split()if int(op) == 1:l, ch = int(a1) - 1, a2[0]trees[l % 3][toId(s[l])].update(l + 1, -1)s[l] = chtrees[l % 3][toId(s[l])].update(l + 1, 1)else:l, r = int(a1) - 1, int(a2) - 1res = inffor (t1, t2, t3) in list(permutations([0, 1, 2])):z1 = trees[(l + t1) % 3][0].query(r + 1) - trees[(l + t1) % 3][0].query(l)z2 = trees[(l + t2) % 3][1].query(r + 1) - trees[(l + t2) % 3][1].query(l)z3 = trees[(l + t3) % 3][2].query(r + 1) - trees[(l + t3) % 3][2].query(l)res = min(res, (r - l + 1) - (z1 + z2 + z3))print (res)