2021-10-12 116. 填充每个节点的下一个右侧节点指针（层序遍历，找规律）

本文主要是介绍2021-10-12 116. 填充每个节点的下一个右侧节点指针（层序遍历，找规律），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

注：

题目：
给定一个 完美二叉树 ，其所有叶子节点都在同一层，每个父节点都有两个子节点。二叉树定义如下：

struct Node {int val;Node *left;Node *right;Node *next;
}

填充它的每个 next 指针，让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点，则将 next 指针设置为 NULL。

初始状态下，所有 next 指针都被设置为 NULL。

进阶：
你只能使用常量级额外空间。
使用递归解题也符合要求，本题中递归程序占用的栈空间不算做额外的空间复杂度。

示例：
输入：root = [1,2,3,4,5,6,7]
输出：[1,#,2,3,#,4,5,6,7,#]
解释：给定二叉树如图 A 所示，你的函数应该填充它的每个 next 指针，以指向其下一个右侧节点，如图 B 所示。序列化的输出按层序遍历排列，同一层节点由 next 指针连接，’#’ 标志着每一层的结束。

提示：
树中节点的数量少于 4096
-1000 <= node.val <= 1000

题解：
方法一 层序遍历
思路与算法
题目本身希望我们将二叉树的每一层节点都连接起来形成一个链表。因此直观的做法我们可以对二叉树进行层次遍历，在层次遍历的过程中将我们将二叉树每一层的节点拿出来遍历并连接。

层次遍历基于广度优先搜索，它与广度优先搜索的不同之处在于，广度优先搜索每次只会取出一个节点来拓展，而层次遍历会每次将队列中的所有元素都拿出来拓展，这样能保证每次从队列中拿出来遍历的元素都是属于同一层的，因此我们可以在遍历的过程中修改每个节点的 \text{next}next 指针，同时拓展下一层的新队列。

复杂度分析
时间复杂度：O(N)。每个节点会被访问一次且只会被访问一次，即从队列中弹出，并建立 next 指针。

空间复杂度：O(N)。这是一棵完美二叉树，它的最后一个层级包含 N/2 个节点。广度优先遍历的复杂度取决于一个层级上的最大元素数量。这种情况下空间复杂度为 O(N)。

/*
// Definition for a Node.
class Node {
public:int val;Node* left;Node* right;Node* next;Node() : val(0), left(NULL), right(NULL), next(NULL) {}Node(int _val) : val(_val), left(NULL), right(NULL), next(NULL) {}Node(int _val, Node* _left, Node* _right, Node* _next): val(_val), left(_left), right(_right), next(_next) {}
};
*/class Solution {
public:Node* connect(Node* root) {queue<Node*> que;if(root==NULL){return root;}else{que.push(root);}while(!que.empty()){int size=que.size();Node* head;for(int i=0;i<size;i++){if(i==0){head=que.front();que.pop();head->next==NULL;}else{Node* temp=que.front();head->next=temp;head=temp;que.pop();}if(head->left!=NULL){que.push(head->left);}if(head->right!=NULL){que.push(head->right);}}}return root;}
};

方法二 找规律
思路

一棵树中，存在两种类型的 next 指针。

• 第一种情况是连接同一个父节点的两个子节点。它们可以通过同一个节点直接访问到，因此执行下面操作即可完成连接。

node.left.next = node.right

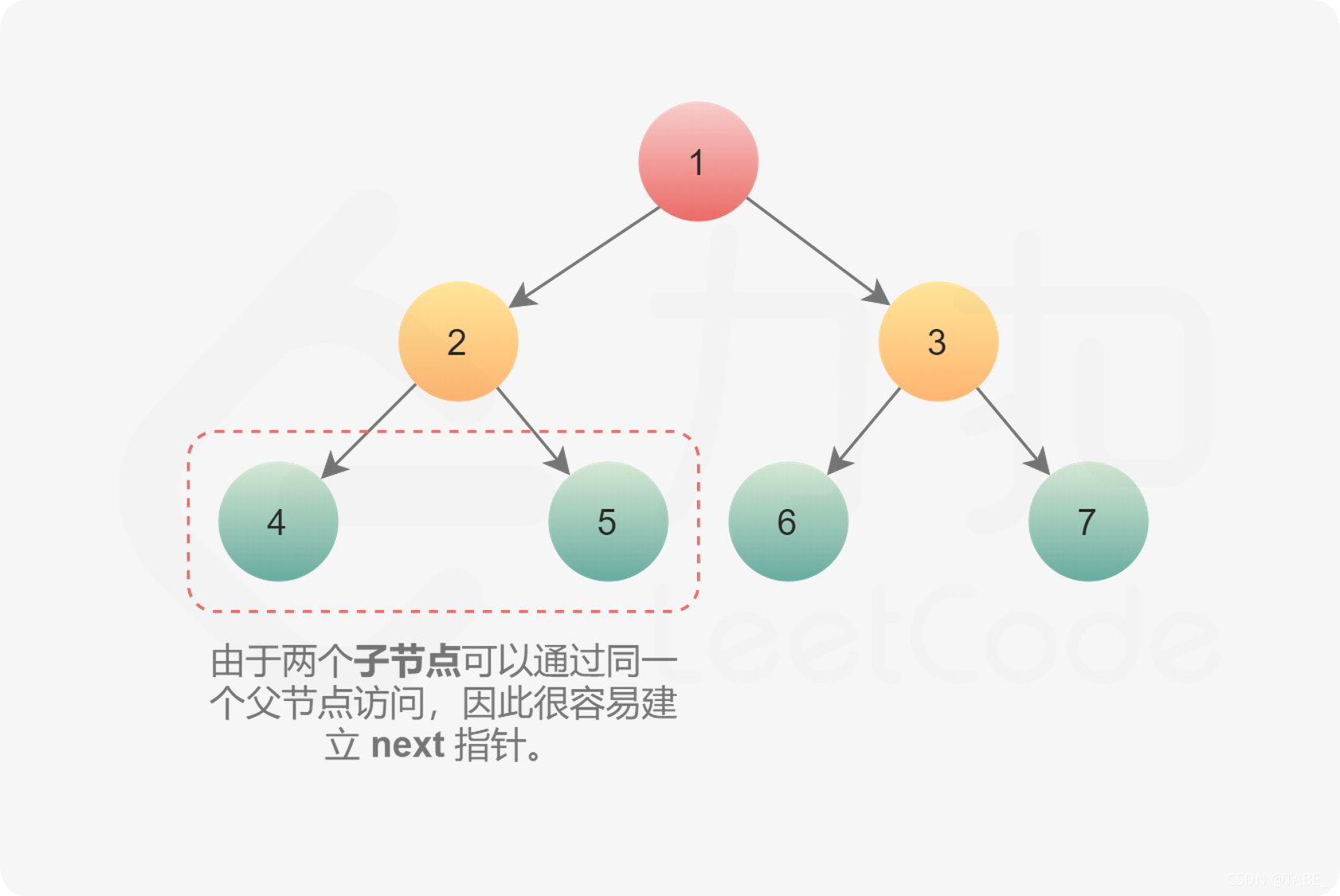
• 第二种情况在不同父亲的子节点之间建立连接，这种情况不能直接连接。

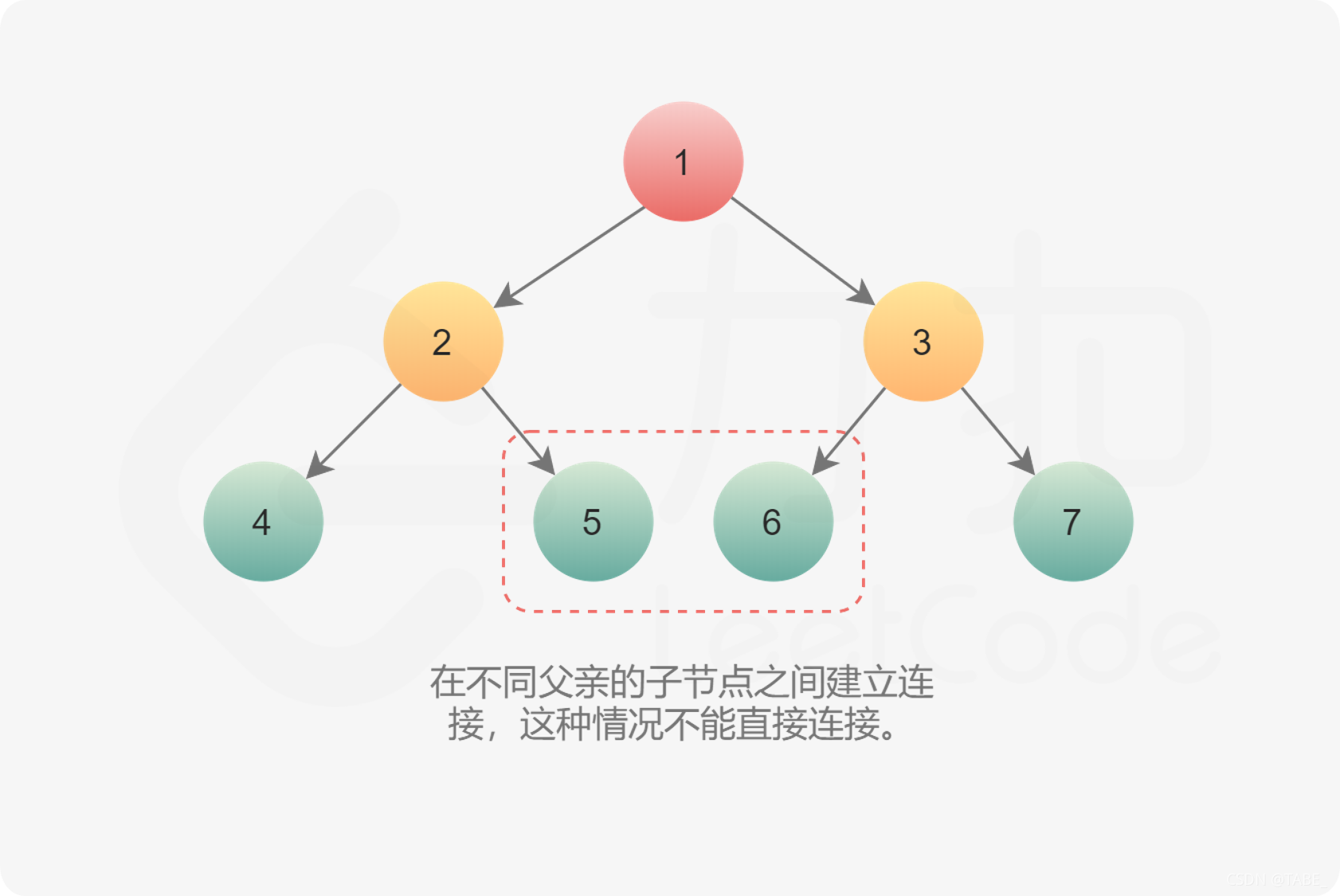
如果每个节点有指向父节点的指针，可以通过该指针找到 next 节点。如果不存在该指针，则按照下面思路建立连接：

第 N 层节点之间建立 next 指针后，再建立第 N+1 层节点的 next 指针。可以通过 next 指针访问同一层的所有节点，因此可以使用第 N 层的 next 指针，为第 N+1 层节点建立 next 指针。

复杂度分析
时间复杂度：O(N)，每个节点只访问一次。

空间复杂度：O(1)，不需要存储额外的节点。

/*
// Definition for a Node.
class Node {
public:int val;Node* left;Node* right;Node* next;Node() : val(0), left(NULL), right(NULL), next(NULL) {}Node(int _val) : val(_val), left(NULL), right(NULL), next(NULL) {}Node(int _val, Node* _left, Node* _right, Node* _next): val(_val), left(_left), right(_right), next(_next) {}
};
*/class Solution {
public:Node* connect(Node* root) {Node* head=root;Node* row=root;while(head!=NULL){while(head!=NULL){if(head->left!=NULL){head->left->next=head->right;}if(head->right!=NULL&&head->next!=NULL){head->right->next=head->next->left;}head=head->next;}head=row->left;row=head;}return root;}
};

这篇关于2021-10-12 116. 填充每个节点的下一个右侧节点指针（层序遍历，找规律）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---