本文主要是介绍图像压缩算法,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
图像压缩
图像压缩算法是对图像在资源空间上的压缩,每一个色块的颜色可以粗略的由红、绿、蓝的各自三个不同的深度合成得来。
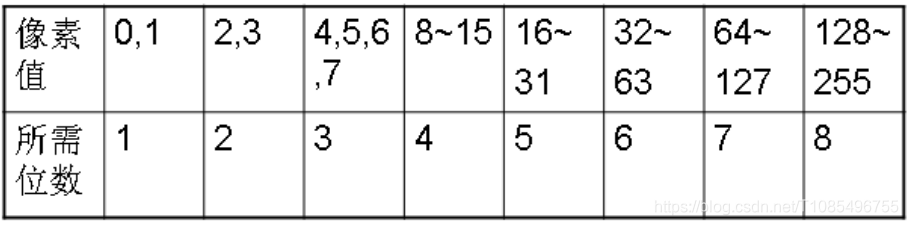
那么,如果我们每一个颜色的程度用8位的二进制码来表示,最终需要24m2大小的空间(这里的m2不是表示平方米,是一种空间大小的计量单位);而如果我们用5位来表示,需要15m2大小的空间。

选用的位数多,图像色彩更加丰富图像会更清晰,可空间上占用太多资源;而位数少,可以节省空间,可图片就会不够清晰。
我们目前的磁盘空间一般都比较大了,空间不再是特别昂贵的资源。可我们需要考虑一些其他的情况,比如我们的一些特殊的原件,内存空间十分有限,那么我们就需要在空间上有所拮据;亦或者我们网页应用,如果图片较大,那么在加载时需要的时间就会增长,体验感上难免不舒服;再者我们的用户量多的服务器,空间总是有限的,如果数量级达到一定程度也是十分恐怖的。
那么总而言之,算法对于程序来说,是十分重要的。也是一个程序品质的真正内核所在!
那么我们接下来就以8位为例,来体会一下这个图像压缩算法。图像压缩的本质实质上来自于动态规划,大家可以在我们之后的过程中慢慢体会。
为了减少空间的消耗,我们尝试一种变长的模式来存储,不同像素采用不同的位数。
1.图像线性化
那么,我们首先要做的是将数据线性化,就是将矩阵式的数字变成线性。
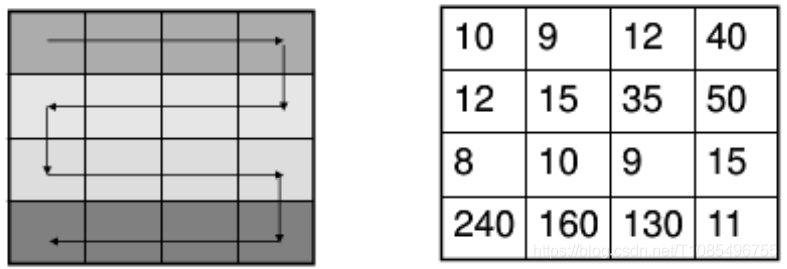
变完之后的效果就是这样:
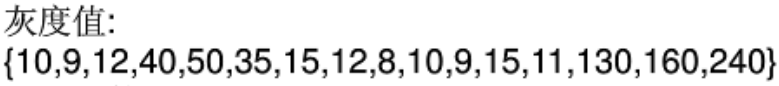
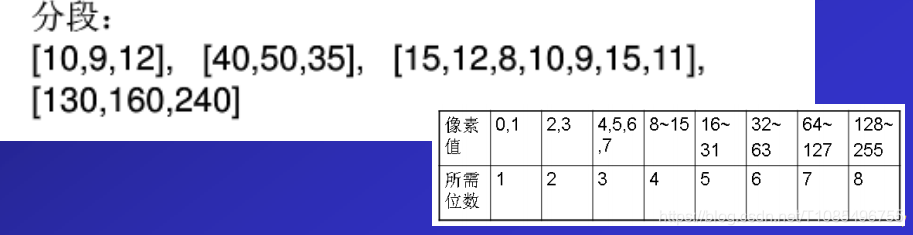
2.分段
接下来,我们对上面整理好的线性数据进行分段。
分段规则如下:
1.每一段中的像素位数设置相同。
2.每段是相邻的几个元素的集合。
3.每段最多含256个元素,若超过就需要增加段来表示。(由于最高位数设置为8)
3.分配空间
我们将数据分好段了,就可以按照之前的这个表查找,这一个段的所有元素,最大需要的存储位数了。那么我们说,只要给这段的每个元素以最大需要的位数空间,那么我们每个元素就都能存的下了。

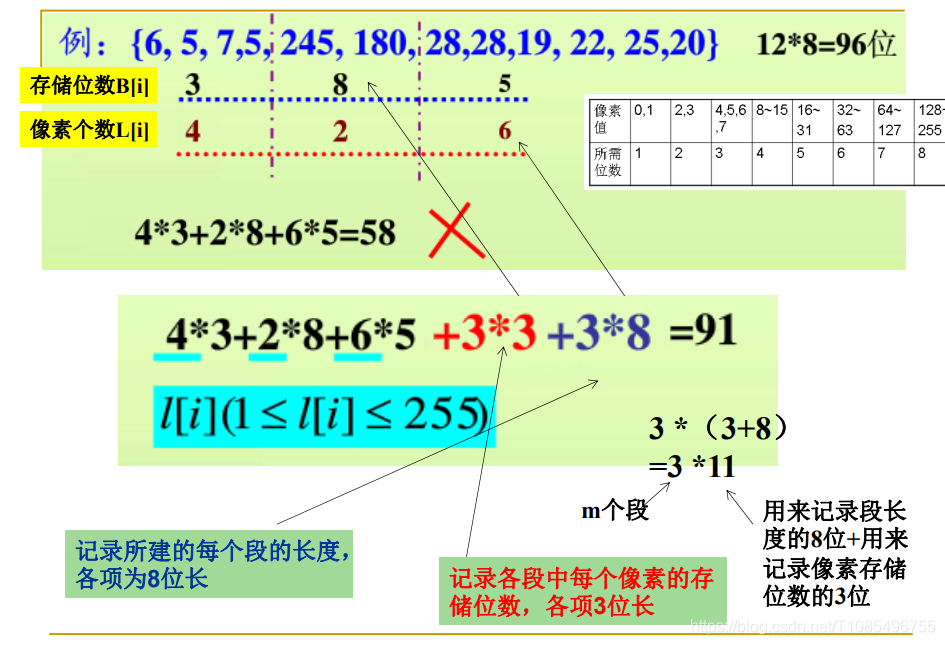
我们再举一个例子:
将这一个集合如图分成三段,然后按照表格记录每一段所需要的存储位数。那么除此之外,我们还需要记录每一段包含了几个元素。
而这两个变量,我们也需要一定的空间存储,每增加一段,就需要一份这样的开销:
段数3+段数8,化简得:段数*11。
3表示:我们每个段所需要的存储位数,最大为8位,那么8这个十进制数,我们需要3位的二进制来表示。
8表示:我们每段包含的元素个数,最大不能超过256(超过就需要两个段了),那么这个十进制的256,需要8位的二进制进行表示。
所以,我们每多分一个段,就会多一个11的开销,这个十一是固定不能变的,而某种意义上,这部分空间就属于被浪费了,因为他没有起到存储图像内容的作用。因此,我们明白了,合理的分段可以节省空间,可盲目对图像分段细化,只会造成过多的11无用开销。
所以,图像压缩算法就是找到一个平衡点,找出最优的分段方案!
这篇关于图像压缩算法的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!









