半诚实模型

The Semi-Honest Model 半诚实模型

半诚实的参与方，遵循了协议的执行，但是却保存了协议的中间计算状态，实际上，半诚实的参与方，只要保存内部的掷硬币过程（产生随机数的过程）和所有从其他参与方接收到的消息就行了。特别是，一个半诚实的参与方会选择随机数和根据预定的程序进行操作，即根据预定的程序公平的产生随机数和执行输入与输出。值得注意的是，一个半诚实参与方相当于是零知识中的诚实验证者。

既然积极的恶意敌手更有攻击能力，那么我们到底为什么还要考虑攻击能力更弱的半诚实模型？即半诚实的敌手模型的必要性在哪里？其实在一般情况下，发动主动攻击要比监听整个计算过程在攻击复杂的多，原因是，对于一个运行在计算机上程序，主动的攻击需要用一些非常复杂的程序去攻击他，但是对于单纯的获取计算过程中的数据而言，这是比较容易的，所以半诚实敌手模型在实际的生产生活中更加的普遍存在，就是单独考虑半诚实敌手的必要性。

接下来我们主要探讨在安全半诚实模型中的两个等价的公式，
1.第一个公式直接推广了零知识的定义的一般性，进一步定义了半诚实模型下的安全性。
2.第二种来源于之前定义的“real VS ideal”方法学。

两种方法都是遵循“模拟范式”，第一种直接来源于零知识的定义，第二种来源于“退化的通用真实-理想模型”
ps:模拟范式（“simulation paradigm”）可能来源于GMW86，这个没看过，还需要确定。

从零知识的角度看半诚实模型

简单的来说，如果一个协议能够保密的计算函数 f , 那么凡是能够从一个参与方视图获得的内容，都能够完全从这个参与方的输入输出获得。

为了描述方面，这里定义一些半诚实的行为：
计算的函数 f : {0,1}* x {0,1}* - > {0,1}* x {0,1}* , 计算结果为 f( x , y）；
其中第一方的计算结果：f1(x , y) 为计算结果的第一个元素；
其中第一方的计算结果：f2(x , y) 为计算结果的第二个元素；
协议PI，是一个两方协议用来计算函数f；
第一方和第二方的视图 VIEW(x, y ) ;(x, r , m1,m2,…,mt), 其中r是一方随机输出，m 为第t次的输出消息。
协议执行完成之后的输出定义为OUTPUT（x,y）

deterministic case 对于确定性的例子

确定性的例子即为，输入确定，则输出时不会变化的。所以只需要考虑模拟器的视图和协议执行的视图即可。

general case 对于确定性的例子

对于通用的例子来说，其实就是，对于概率性的算法，每次的输出可能是不相同的，所以需要对比模拟器的视图和协议执行者的视图。其中式子右边的这个四部分内容都是相关的随机数，被定义来源于相同的随机过程，特别是，OUTPUT完全是相应的由视图VIEW定义。

基于零知识原语的模拟

首先考虑一个确定性的例子，由式子7.8 7.9 来看，能够都有效的模拟，完全取决于他自己的输入和输出。也就是说参与方能够从执行过程中获得所有的信息本质上都包含在他本身的输入和输出中。对于确定的函数来说，存在以下的内容：

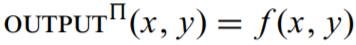
协议的输出和函数的输出相等。

和确定性函数相反的情形就是通用的情形，涉及到随机的计算过程时，输出不一定要满足上图中，协议的输出和函数的输出相等的关系。因为每一方都是输随机的，确实，这两个随机的值必须是分