本文主要是介绍Physical Based Rendering 第一章 简介,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
Physical Based Rendering 第一章 简介
- 前言
- 光是什么
- 相机和电影
- 光线物体的交互
- 光的分布
- 可见性
- 表面光的散射
- 间接光照
- 射线传播
前言
丢个连接
光是什么
如果说,我们想要让一张图片无法分辨是真是假,那么光的模拟肯定是首当其冲的。想要模拟光,我们自然而然会有一个疑问:光是什么?
根据物理学研究,我们认为光具有“波粒二象性”,即其即可以看作电磁波的形式进行传播,也具有光子的粒子性。
那么为了模拟光,我们需要怎么利用这种性质呢?好消息是,我们所需模拟的光,实际上只是所有波谱中非常小的一部分(可见光)。除此之外,我们知道光的波长很小,在实际过程中,我们所模拟的物体大多以厘米或米计,这实际上是一个好消息,因为这种情况使得我们没有必要去追踪光线的波层面的细节(如果需要追究这种细节,计算机图形学渲染早就不存在了)。在计算机图形学中,我们遵从16或17世纪的物理学模型,将光看作粒子,追踪其运动轨迹。
这一做法实际上后来也成为了知名的算法:光线追踪。
从原理而言,光追实际上模拟了光线与物体交互和脱离的过程。但是无论一个光追系统如何设计,其体系中总是包含如下元素:
- 相机:决定了图像是从哪个角度观察的。
- 光线与物体的互动
- 光源
- 可见性
- 表面上光的散射
- 间接的光路
- 光线传播
相机和电影
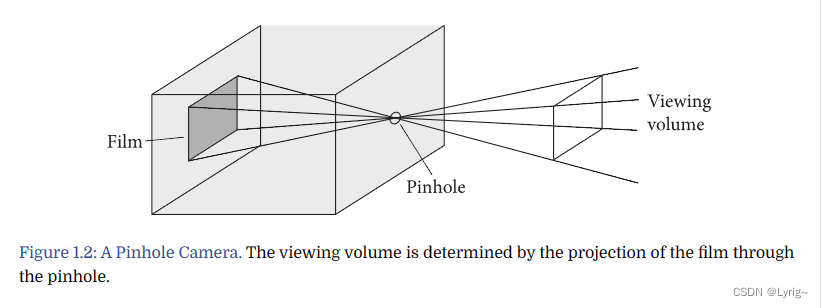
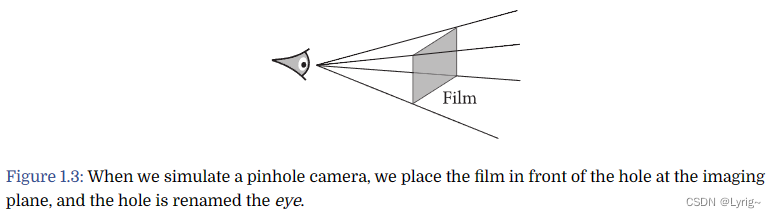
光线物体的交互
每当相加生成一条光线,首先需要确认的是,这条光线是否与物体有碰撞,以及碰撞的位置在哪。对于一条光线 r r r:
r ( t ) = o + t d r(t)=o + t\bold{d} r(t)=o+td
其中 o o o是光线的起始位置, d \bold{d} d为光线的方向。 t t t作为参数,范围为 [ 0 , + ∞ ] [0,+\infty] [0,+∞]。
对于一个平面 F ( x , y , z ) = 0 F(x,y,z)=0 F(x,y,z)=0,光线碰撞满足以下方程:
x 2 + y 2 + z 2 − r 2 = 0 x^2 + y^2 + z^2 - r^2 = 0 x2+y2+z2−r2=0
然而实际中,我们通常用一个含有t的方程来替代:
( o x + t b x ) 2 + ( o y + t b y ) 2 + ( o z + t b z ) 2 − r 2 = 0 (o_x + t\bold{b}_x)^2+(o_y + t\bold{b}_y)^2+(o_z + t\bold{b}_z)^2-r^2=0 (ox+tbx)2+(oy+tby)2+(oz+tbz)2−r2=0
对这个方程求解,如果t没有实属根,则说明光线错过了这个球面,反之则说明相交。且最小的实根就是第一个交点。

光的分布
虽然点光源在现实中并不存在,且在实际算法中,使用面光源会更合理。但是本节为了方便期间,还是使用点光源模型进行描述。
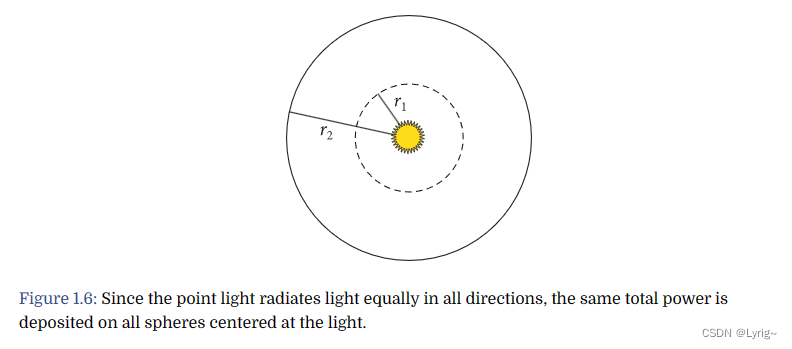
我们假设点光源的对周围是均匀发光,则对单位球面,单位面积的照射强度为 Φ 4 π \frac{\Phi}{4\pi} 4πΦ,对于距离如下的两个球面,半径分别为 r 1 , r 2 r_1,r_2 r1,r2,我们很容易能看出,照射强度实际上与 1 r 2 \frac{1}{r^2} r21成正比。
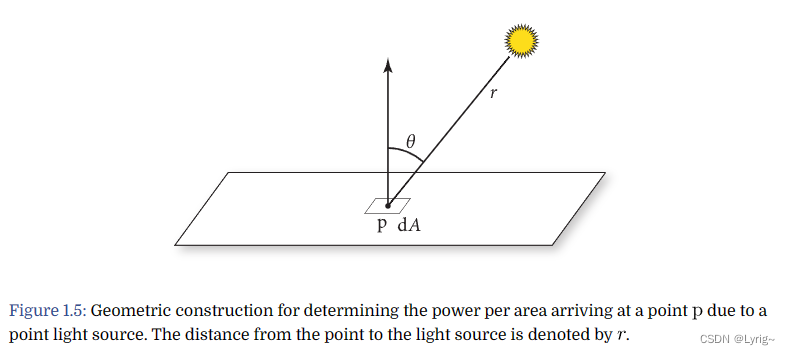
同理,对于任何一个单位面积 d A dA dA,其与光线成 θ \theta θ角度,其微分形式的能量强度为(辐射度):
d E = Φ c o s θ 4 π r 2 dE=\frac{\Phi cos\theta}{4\pi r^2} dE=4πr2Φcosθ
上式实际上包含了两条基本定理:倾斜表面的光的余弦损失,以及距离平方衰减。
可见性
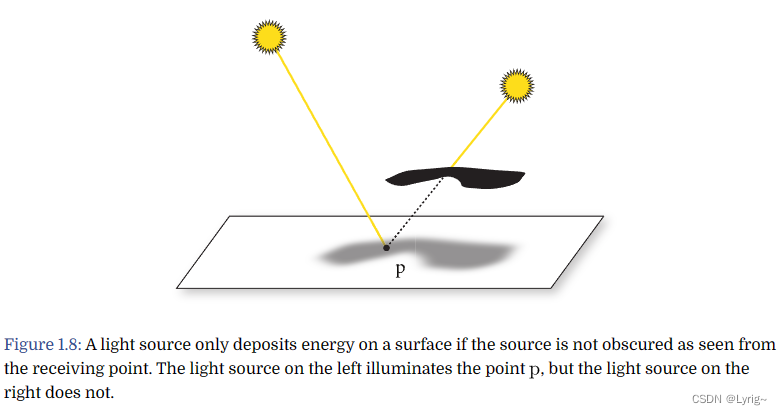
表面光的散射
在我们能够正确计算得到某个表面是否有入射光之后,我们下一步需要知道,该表面的入射光如何散射,我们需要了解散射的能量分布,尤其是那些进入相机的散射能量。
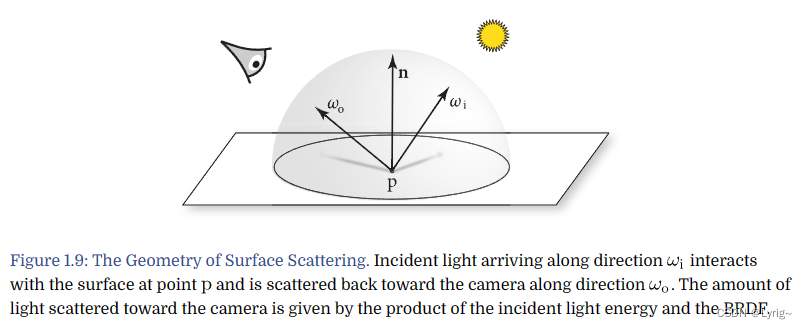
场景中每个物体都会具有一个材质,其效果为具有一个双向反射比分布函数(BRDF),这个方程向我们解释了从入射角度 ω i \omega_i ωi到任意出射角度 ω o \omega_o ωo的能量反射。在p点处的BRDF函数我们可以写作: f r ( p , ω i , ω o ) f_r(p, \omega_i, \omega_o) fr(p,ωi,ωo)。
受到上述方式的启发,我们同样可以针对散射、透射定义相关的函数(BSDF、BTDF)。
间接光照
某个点的光照能量可以看作是直接入射到这一点的光照与其它散射光照的和。这一想法可以写作如下光线转移方程:
L o ( p , ω o ) = L e ( p , ω o ) + ∫ S 2 f ( p , ω o , ω i ) L ( p , ω i ) ∣ c o s θ i ∣ d ω i (1.1) L_o(p, \omega_o)=L_e(p,\omega_o) + \int_{S^2}{f(p,\omega_o,\omega_i)L(p,\omega_i)|cos\theta_i|d\omega_i}\tag{1.1} Lo(p,ωo)=Le(p,ωo)+∫S2f(p,ωo,ωi)L(p,ωi)∣cosθi∣dωi(1.1)
其描述了在p点处沿 ω o \omega_o ωo角度的辐射度 L o ( p , ω o ) L_o(p, \omega_o) Lo(p,ωo)为,该点本身发光发出的辐射度 L e ( p , ω o ) L_e(p,\omega_o) Le(p,ωo)加上由环境其它地方沿 ω i \omega_i ωi散射到p点的散射光 L ( p , ω i ) L(p,\omega_i) L(p,ωi)再利用光线转移方程得到的光线,其中积分区域 S 2 S^2 S2为p点附近极小的一个球面,其 θ i \theta_i θi即为入射的散射光线与球面的散射角。
射线传播

前文的描述实际上有一个默认的假设,即光线全部再真空中传播。例如当我们讨论光在在球面的出射,实际上我们并未考虑光在传播过程中的衰减。烟雾、尘埃、雾气都会让这些假设失效。
这篇关于Physical Based Rendering 第一章 简介的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








