本文主要是介绍【算法笔记】枚举之熄灯问题,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
在学北大郭玮和刘家瑛老师的算法基础,做点笔记
题目:
有一个5*6矩阵的按钮,每个按钮对应一盏灯,每按下一个按钮,这个按钮对应的灯的上下左右的灯都会改变一次状态,通过输入的灯的状态,要求输出能使所有灯熄灭的按钮解决方案
解决思路1:
枚举所有可能,将按钮所有可能的状态枚举出来,从而找到符合条件的组合。
这种思路简单粗暴,但是有总共有30个按钮,要枚举2的30次方种情况,会导致超时。
解决思路2:
存在一个部分,当这个部分一旦确定,那剩余部分的状态只能是一种或较少的n种。
这里确定的这个部分可以第一列或者第一行。自上而下确定方案。
由于当一个按钮被按下,那么它只能控制它上一行(列)对应的那盏灯。
这里先以确定第一行的策略简单描述下:
当第一行的按钮状态被确定后,要将第一行还未熄灭的灯熄灭,则第二行也确定,第二行确定后,要讲第二行还未熄灭的灯熄灭,则第三行的解决方案也唯一……如此推下去,则最后一行也确定了,这时判断最后一行是否已经灯全熄灭,若全熄灭,则这就是正确的解决方案,如果没有全熄灭,则改变第一行的按钮状态,循环判断。
这种思路,只需要枚举第一行的情况,共有2的6次方种情况,大大减少了计算机的负担,提高了效率
有了大致的思路框架后,来看细节方面的问题:
需解决问题1:当按钮所在位置不同时,能操纵的灯也是不同的,特殊的位置有角和边:
在四个角位置上的按钮只能控制三盏灯:

在边位置上只能控制四盏灯

在除去边角的位置上都能控制无盏灯

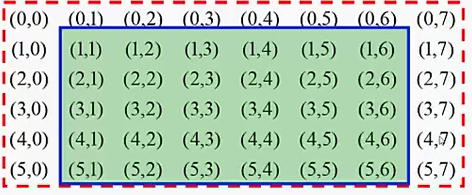
为了排除这个特殊性,我们将这个矩阵扩展为6*8矩阵
其中1<=x<=5与y<=1<=6的位置是我们的按钮矩阵,其他位置都置零,这样不用分情况讨论我们的按钮按下发生的情况。
需解决问题2:怎么根据上一行的按钮状态以及灯的状态来确定下一行的按钮状态
press[i+1][j] = (puzzle[i][j] + press[i][j] + press[i][j-1] + press[i][j+1] + press[i-1][j]) % 2;因为本行要设置的按钮状态只与此按钮头顶上那个灯当前的状态有关,而头顶上那个灯当前的状态与其自己灯本身的状态以及其对应按钮的状态及其上、左、右三个按钮的状态有关。因此得到通过这五种状态的和余2得到其当前状态,如果头顶上那个灯当前状态为0,则我们不需要按下按钮,按钮状态也为0,如果头顶上那个灯是亮着的,状态为1,则我们需要按下按钮,按钮状态也为1.
需解决问题3.怎么判断是否最后一行(第五行)灯状态为全熄灭:
if( puzzle[5][i] != (press[5][i] + press[4][i] + press[5][i-1] + press[5][i+1] ) %2);最后一行的灯只受其上、左、右及其自己的按钮状态以及这个灯原本的状态影响。
当前灯熄灭的两个条件:
1.如果受到了按钮组合的影响(这几个按钮被按下的数目为奇数)((press[5][i] + press[4][i] + press[5][i-1] + press[5][i+1] ) %2==1),则需要这个灯原本状态为亮(puzzle[5][i]==1).
2.1.如果没受到按钮组合的影响(这几个按钮被按下的数目为偶数)((press[5][i] + press[4][i] + press[5][i-1] + press[5][i+1] ) %2==0),则需要这个灯原本状态为熄灭(puzzle[5][i]==0).
需解决问题4:怎么枚举出第一行的按钮状态
press[1][1]-press[1][6]的状态
0 0 0 0 0 0
1 0 0 0 0 0
0 1 0 0 0 0
1 1 0 0 0 0
0 0 1 0 0 0
……
1 1 1 1 1 1这里可以模拟二进制数:
从000000开始枚举,每次将press[1][1]加一,然后循环判断,只要当前位为2,则置当前位为0,下一个位加1...直到枚举完毕
代码:
#include <stdio.h>int puzzle[6][8], press[6][8]; //puzzle为灯的状态矩阵,0表示熄灭,1表示亮;press为按钮状态矩阵,0表示没按下,1表示按下
typedef int bool;
bool guess()
{int c, r;//先根据第一行的状态依次推算出其余部分状态for (c = 1; c < 5; c++){for (r = 1; r < 7; r++){press[c + 1][r] = (puzzle[c][r] + press[c][r - 1] + press[c][r + 1] + press[c][r] + press[c - 1][r]) % 2;}}//判断第五行是否全部熄灭,从而判断该方案是否符合条件for (c = 1; c < 7; c++){if (puzzle[5][c] != (press[5][c] + press[4][c] + press[5][c - 1] + press[5][c + 1]) % 2)return 0;}return 1;
}void enumerate()
{int c;//将要第一行初始化为0 0 0 0 0 0for (c = 1; c < 7; c++){press[1][c] = 0;}//如果当前枚举的按钮状态不能使灯全熄灭,则继续枚举新的情况while (guess() == 0){press[1][1]++;c = 1;while (press[1][c] > 1) //判断当前位是否大于1,大于1则进位,且继续判断下一位,直到不需进位{press[1][c] = 0;c++;press[1][c]++;}}return;
}
int main()
{int cases, i, r, c;scanf("%d", &cases);//将第0列及第7列的元素置0,这两列不能代表实际的按钮状态for (r = 0; r < 6; r++){press[r][0] = press[r][7] = 0;}//将第0行的press状态置0,这一行不能代表实际的按钮状态for (c = 1; c < 7; c++){press[0][c] = 0;}for (i = 0; i < cases; i++){for (r = 1; r < 6; r++){for (c = 1; c < 7; c++){scanf("%d", &puzzle[r][c]);}}//为当前case寻找解决方案enumerate();printf("puzzle#%d\n", i + 1);for (r = 1; r < 6; r++){for (c = 1; c < 7; c++){printf("%d ", press[r][c]);}printf("\n");}}return 0;
}这篇关于【算法笔记】枚举之熄灯问题的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!