本文主要是介绍Leetcode - 周赛387,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
一,3069. 将元素分配到两个数组中 I
二,3070. 元素和小于等于 k 的子矩阵的数目
三,3071. 在矩阵上写出字母 Y 所需的最少操作次数
四,3072. 将元素分配到两个数组中 II
一,3069. 将元素分配到两个数组中 I

本题数据范围较小,纯模拟,代码如下:
class Solution {public int[] resultArray(int[] nums) {int n = nums.length;List<Integer> a = new ArrayList<>();List<Integer> b = new ArrayList<>();a.add(nums[0]);b.add(nums[1]);for(int i=2; i<n; i++){int t = a.get(a.size()-1) - b.get(b.size()-1);if(t > 0)a.add(nums[i]);elseb.add(nums[i]);}a.addAll(b);for(int i=0; i<n; i++){nums[i] = a.get(i);}return nums;}
}二,3070. 元素和小于等于 k 的子矩阵的数目
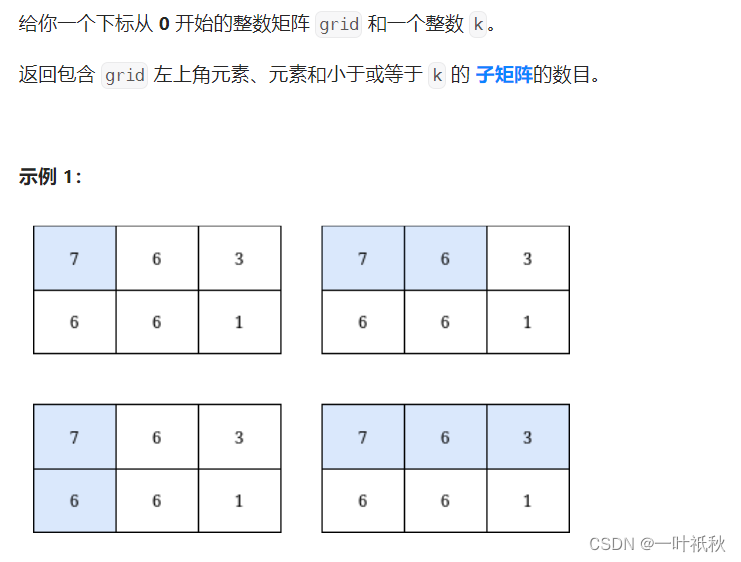
本题的主要考点在于求二维数组的前缀和,这里有两种写法:
1)递推
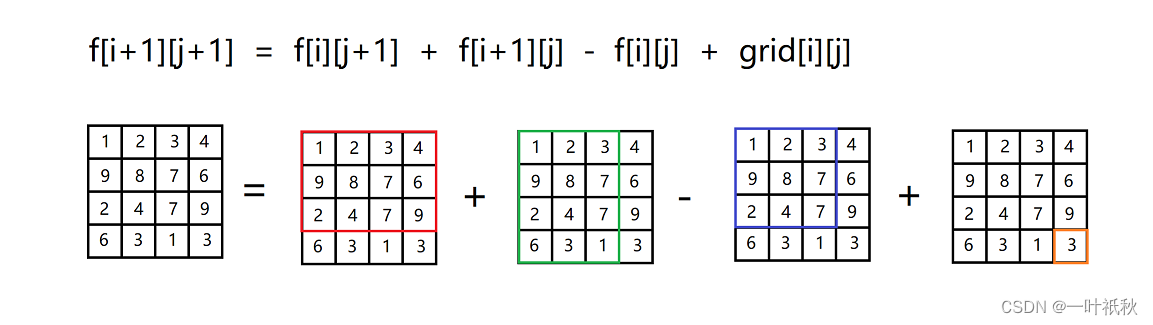
class Solution {public int countSubmatrices(int[][] grid, int k) {int n = grid.length;int m = grid[0].length;int ans = 0;int[][] f = new int[n+1][m+1];//这样初始化是防止f[i][j]中的i,j出现负数的情况for(int i=0; i<n; i++){ for(int j=0; j<m; j++){f[i+1][j+1] = f[i][j+1] + f[i+1][j] - f[i][j] + grid[i][j];if(f[i+1][j+1]<=k)ans++;}}return ans;}
}2)由一维前缀和推导而来,本质还是递推
先用一个数组计算每一行的前缀和,再用一个数组来统计前 i 行 j 列的元素和
class Solution {public int countSubmatrices(int[][] grid, int k) {int n = grid.length;int m = grid[0].length;int ans = 0;int[] sum = new int[m];//第i行的前缀和int[] pre_sum = new int[m];//前 i 行 前 j 列的元素前缀和for(int i=0; i<n; i++){ for(int j=0; j<m; j++){sum[j] = (j>0?sum[j-1]:0) + grid[i][j];pre_sum[j] += sum[j];if(pre_sum[j]<=k){ans++;} }}return ans;}
}三,3071. 在矩阵上写出字母 Y 所需的最少操作次数

数据范围小,纯模拟题,代码如下:
class Solution {//正难则反//求最少操作次数 -> 总数 - 最大的不操作次数public int minimumOperationsToWriteY(int[][] grid) {int[] left = new int[3];统计剩下的形状中0,1,2各出现的次数int[] y = new int[3];//统计y形状中0,1,2各出现的次数int n = grid.length;for(int i=0; i<n; i++){for(int j=0; j<n; j++){if(i<=n/2&&(i==j||i==n-j-1)||i>n/2&&j==n/2){y[grid[i][j]]++;}else{left[grid[i][j]]++;}}}int ans = Math.max(y[0]+left[1], y[0]+left[2]);ans = Math.max(y[1]+left[0],Math.max(ans, y[1]+left[2]));ans = Math.max(y[2]+left[0],Math.max(ans, y[2]+left[1]));return n*n-ans;}
}四,3072. 将元素分配到两个数组中 II

本题需要维护一个动态的前缀和,如果使用一个链表,那么他的查找和添加操作需要O(n)的时间,再加上遍历nums所需要的O(n)时间,也就是说需要O(n^2)的时间复杂度,这肯定会超时,所以这里使用了树状数组的数据结构。
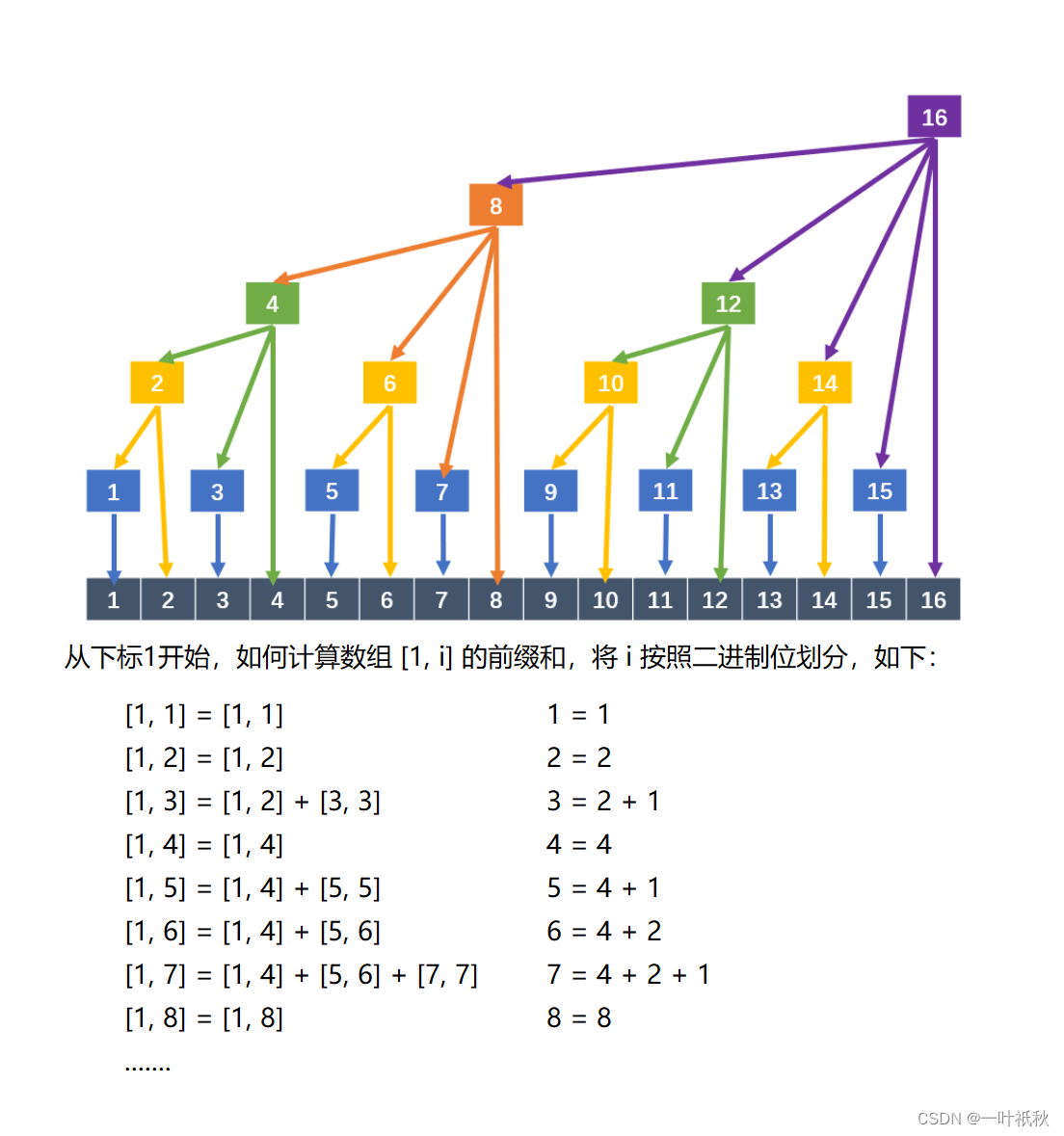
在讲思路之前,先简单介绍一下树状数组:树状数组是解决数据压缩里的累积频率的计算问题,多用于高效计算数列的前缀和, 区间和。
画个图了解一下:
思路:创建两个树状数组,通过当前树状数组的前缀和来统计有多少数小于当前遍历的nums[i],同时把nuns[i]添加进其中满足题目条件的树状数组中,为了减少空间复杂度,还可以使用离散化,因为题目中只要求比较大小,比如说:5 和 10 比较大小, 与 1 和 2 比较大小的结果并无区别,也就是说将 5 和 10 替换成 1 和 2 对题目也没有影响,因此可以将nums排序,再使用下标代替原本的值(注意,树状数组的下标是从1开始的,所以要统一加一)。
代码如下:
class Solution {static class Fenwick{//树状数组int[] tree;public Fenwick(int n){tree = new int[n];}public void add(int i){while(i < tree.length){tree[i]++;i += i & -i;}}public int pre(int i){int res = 0;while(i > 0){res += tree[i];i &= i-1;}return res;}}public int[] resultArray(int[] nums) {int n = nums.length;List<Integer> a = new ArrayList<>();List<Integer> b = new ArrayList<>();Fenwick a1 = new Fenwick(n+1);Fenwick b1 = new Fenwick(n+1);a.add(nums[0]);b.add(nums[1]);int[] tmp = nums.clone();Arrays.sort(tmp);a1.add(binarySearch(tmp, nums[0])+1);b1.add(binarySearch(tmp, nums[1])+1);for(int i=2; i<n; i++){int x = nums[i];int v = binarySearch(tmp, x)+1;int a2 = a.size() - a1.pre(v);int b2 = b.size() - b1.pre(v);if(a2>b2 || a2==b2&&a.size()<=b.size()){a.add(x);a1.add(v);}else{b.add(x);b1.add(v);}}a.addAll(b);for(int i=0; i<n; i++)nums[i] = a.get(i);return nums;}int binarySearch(int[] arr, int tar){//二分查找+离散化int l = 0;int r = arr.length-1;while(l <= r){int mid = l+(r-l)/2;if(arr[mid]>tar){r = mid - 1;}else{l = mid + 1;}}return l-1;}
}这篇关于Leetcode - 周赛387的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!