2575. 找出字符串的可整除数组（Go语言）

本文主要是介绍2575. 找出字符串的可整除数组（Go语言），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

https://leetcode.cn/problems/find-the-divisibility-array-of-a-string/

在这里插入图片描述

在看题解之前，我的代码是以下这样：

package mainimport ("fmt"
)func main() {fmt.Println(divisibilityArray("998244353", 3))
}func divisibilityArray(word string, m int) []int {result := make([]int, len(word))sum := 0for i, num := range word {sum = sum*10 + int(num-'0')//fmt.Println(sum)if sum%m == 0 {result[i] = 1} else {result[i] = 0}}return result
}

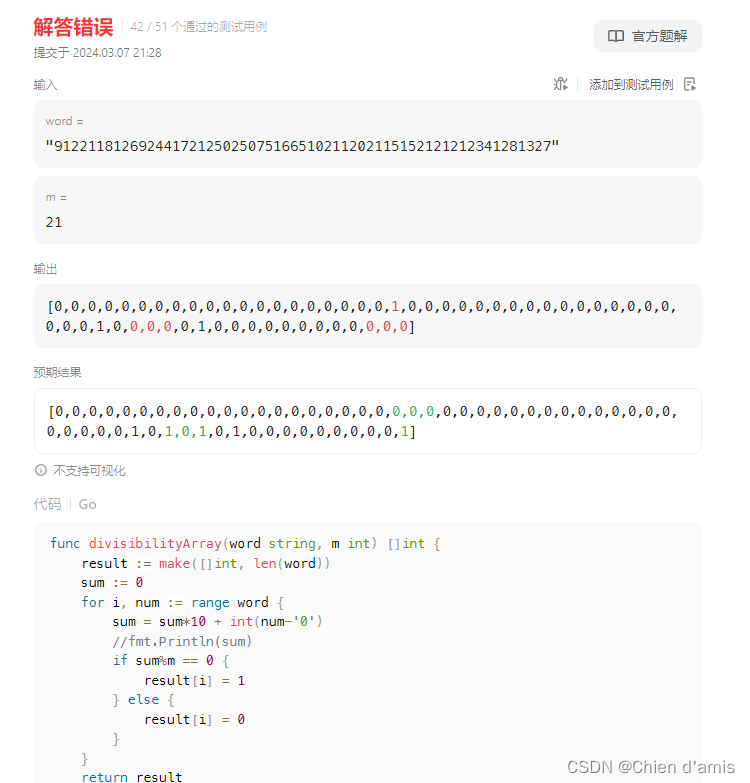
在这里插入图片描述

在运行时，会卡在当前数据上，看逻辑，总觉得没有问题，但会出现如此结果，只好去翻看官解，官方的答案思路如下：

func divisibilityArray(word string, m int) []int {result := make([]int, len(word))sum := 0for i, num := range word {sum = (sum*10 + int(num-'0'))%m//fmt.Println(sum)if sum == 0 {result[i] = 1} else {result[i] = 0}}return result
}

从代码上看，区别在if里面去%求余和在sum计算时求余的区别，后来在单步执行的时候，猛然发现其中的区别：
第一个代码中，sum在每次循环中都被累加，只有在进行条件判断时才对m取模。这意味着sum的值可能会迅速增长，尤其是当word表示一个非常大的数时。这种方法的缺点是，如果word足够长，就可能导致sum变量溢出（超过Go语言整数类型可以表示的最大值），从而导致错误的结果。
第二个代码中，每次循环迭代都会先计算(sum*10 + int(num-‘0’))，然后立即对m取模来更新sum。这种方法的优点是sum的值永远不会超过m的值，有效避免了整数溢出的问题，尤其是当处理非常大的数字时。这也意味着即使是非常长的word字符串，这段代码也能正确运行而不会因为整数溢出而失效。

总结