本文主要是介绍LCR 167. 招式拆解 I,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!


解题思路:
动态规划+哈希表
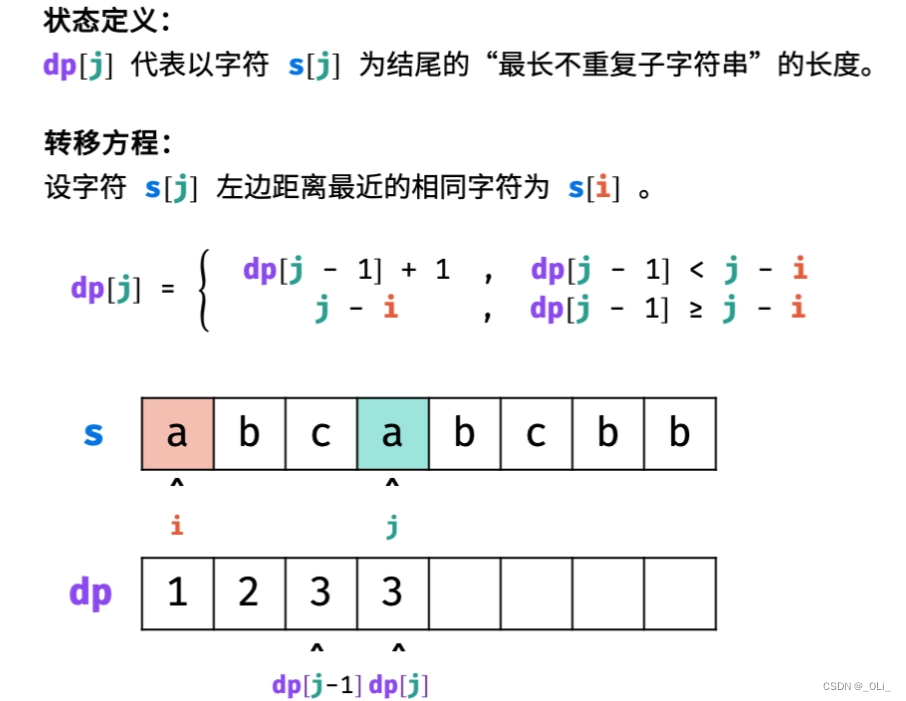
dp[ j ]指的是以字符s[ j ]结尾的字符串的长度。这个字符串不能含有重复字符。
我们可以记为字符串sub[ j ], 该字符串以字符s[ j ]结尾,长度为dp[ j ]。
这样就比较好理解状态转移方程了。固定右边界 j ,同时定义从边界 j 往左侧距离最近的相同字符的索引为 i 。
以字符s[ j - 1 ]结尾的字符串记录为sub[ j - 1],其长度为dp[ j - 1 ],注意sub [ j - 1]中字符不重复。 我们看索引 j 的情况:在 j 的左侧寻找一个重复的字符s [ i ],那么索引 i 可能在字符串sub[ j - 1]的区间内,也可能在字符串sub[ j - 1]的左边界更左侧才有可能寻找到。这样就需要分两种情况考虑。
如果字符 s[ i ] 在子字符串 sub[ j − 1 ] 区间之外,也就是更左侧, 那么dp[ j - 1 ] < j - i,这种情况下,由于sub [ j - 1]中字符不重复,且当前最长,所以以s[ j ]为结尾的字符串只需要在子字符串 sub[ j − 1 ]后面接上这个字符s[ j ]就可以了,其长度dp [ j ] = dp[ j - 1 ] + 1;
如果字符 s[ i ] 在子字符串 sub[ j− 1 ] 区间之中,必然dp[ j−1 ] ≥ j − i,这种情况下,由于我们需要寻找以s[ j ]结尾且最长的字符串,那么sub[ j ]的左边界只能是 i 了,其长度 dp[ j ] = j − i 。
下面举个例子,比如“abcdbaa”,索引从0开始。 我们容易得到,当 j = 4时,以s[4]结尾字符串sub[4] = “cdb”的 长度dp[4] =3。 接下来我们看 j +1的情况。根据定义,sub[4]字符串中的字符肯定不重复,所以当 j = 5时,这时距离字符s[5]的左侧的重复字符a的索引 i = 0, 也就是说s[ 0 ]在子字符串sub[ 4 ]之外了,以s[5]结尾的字符串自然在sub[4]的基础上加上字符s[5]就构成了新的最长的不重复的子串sub[5],长度dp[5] = dp[4] + 1; 接下来我们继续看 j =6的情况,这时s[6]的左侧重复字符a的索引 i = 5,该重复字符在sub[ 5 ]中。新的最长不重复的字串sub[6]左边界以 i 结尾,长度dp[6] = j - i = 1。
abcdbaa
0123456
前置知识:
int i = dic.getOrDefault(arr.charAt(j), -1);
在dic中查找arr.charAt(j),如果存在返回索引,不存在就返回-1(第二个参数设定的值)
dic 这个名字是 “dictionary”(字典)的缩写,字典是一个常见的数据结构,允许以键-值对的形式存储和检索数据。在 Java 中,HashMap 实现了类似字典的功能,因此这里的 dic 就是被用作字典(键-值对映射)来追踪字符和他们最后一次出现的索引。
class Solution {public int dismantlingAction(String arr) {Map<Character, Integer> dic = new HashMap<>();int res = 0;int len = arr.length();int[] dp = new int[len];for (int j = 0; j < len; j++) {// 获取dic中对应键的值,即索引 iint i = dic.getOrDefault(arr.charAt(j), -1); // 更新哈希表,保证字符的索引始终在最新出现的相同字符的位置上,如babce,b的索引先是0,后是2dic.put(arr.charAt(j), j); if (j == 0) {dp[j] = 1; // 初始化dp[0]} else if (dp[j - 1] < j - i) {dp[j] = dp[j - 1] + 1; // dp[j - 1] -> dp[j]} else {dp[j] = j - i; // 新的子字符串开始的位置}res = Math.max(res, dp[j]); // 更新结果}return res; // 返回最长不重复子串的长度}
}这篇关于LCR 167. 招式拆解 I的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!