论文笔记：Burst Denoising with Kernel Prediction Networks

Introduction

这是UC Berkeley与Google Research于CVPR2018发表的一篇多图像去噪论文。其提出了一种CNN网络结构可以预测空间变化的核（kernel），利用得到的每个位置的Kernel对图像进行局部配准和降噪。文章基于真实噪声生成模型对ground truth图像加噪声和偏移，合成训练数据，并利用退火损失函数来引导优化过程，避免陷入局部最小值。
该文章的主要贡献在于：

• 将互联网上获得的经过后处理的图像，转换成具有线性RAW图像特性的数据。这使得训练模型可以推广到真实图像和环境中，解决了ground truth数据难以获取的问题。
• 提出了一种网络结构，其性能在合成数据和真实数据上都优于现有水平。其可以对每个位置生成一个3D去噪核，从而生成去噪图像。
• 提出了一种针对于该核预测网络的训练流程，使得网络可以利用多张图像的信息来预测滤波核，即使这些图像之间存在着未知的偏移。
• 证明了在训练和测试时，将输入图像的噪声水平作为网络的输入，得到的网络将会对更宽的的噪声水平范围具有鲁棒性。

Problem specification

文章的目标是通过手持相机获取的多张有噪声图像，然后生成一张“干净”的图像。
所有的输入图像都在线性RAW空间，不经过图像后处理流程从而避免信息的丢失。

RAW数据特性

RAW数据的噪声主要来自于两方面：

• shot noise：其服从泊松分布，且方差等于信号水平。
• read noise：近似服从高斯分布，其由多种传感器读出效应造成。

这些噪声可以通过一个信号依赖的高斯分布来建模：
$$x_p\sim \mathcal{N}(y_p,{\sigma }_r^2+{\sigma }_s{y}_p)$$

其中，$x_p$是位于像素$p$位置的真实亮度$y_p$的一个噪声测量。噪声参数${\sigma }_r$和${\sigma }_s$对于每张图片是固定的，其只随ISO变化而改变。

合成训练数据

文章使用Open Images dataset中的图像，适当的引入偏移和噪声合成训练数据，模拟真实图像序列的特性。
为了生成N帧图像序列，文章利用一张图像生成N张裁剪图像，各帧之间的裁剪存在随机偏移${\Delta }_i$，其服从2D均匀整数分布。然后对这些裁剪图像在每个维度上使用box filter下采样4倍，从而减少噪声并压缩artifacts。限制下采样后的裁剪图像与参考图像之间最大存在$\pm 2$像素的偏移。
为了模拟由于存在大位移而配准失败的情况，对于每一图像序列随机挑选$n\sim Poisson(\lambda )$帧，在下采样后做最大$\pm 16$像素的偏移。对于8帧的图像序列，$\lambda =1.5$。
为了生成噪声，先把裁剪图像做逆gamm校正，使其转换到近似线性颜色空间。然后线性放缩数据，缩放比例从$[0.1,1]$区间中随机采样，避免数据出现高亮截止区域。最后，通过从真实数据中观察到的噪声参数关系中，采样得到${\sigma }_r$和${\sigma }_s$。利用上述噪声模型对图像序列添加噪声。

Model

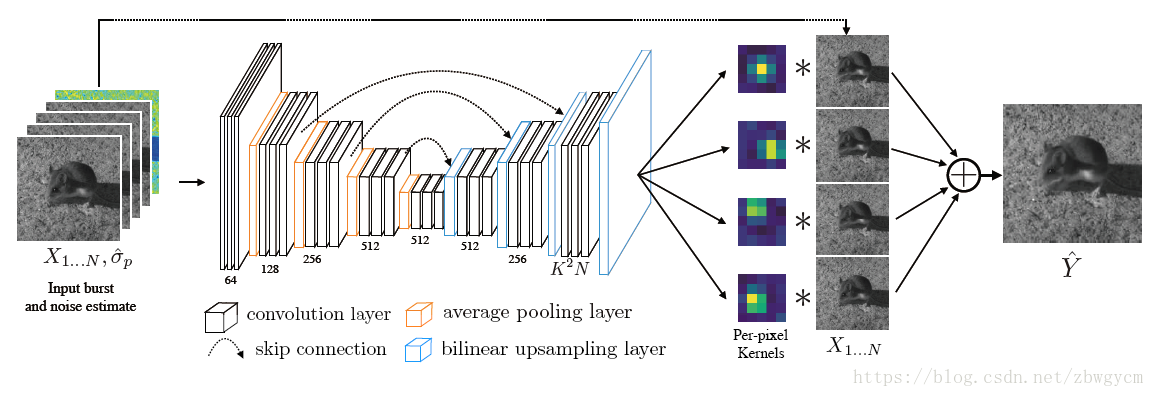
核预测网络（KPN）生成逐像素滤波核，同时对序列图像进行配准，平均，去噪，生成参考帧的“干净”版本。
KPN使用了encoder-decoder结构，并有skip connection。其有$K^{2}N$个输出通道，其可以被变形为$N$个$K\times K$大小线性滤波器。输出$\hat{Y}$的每个像素值为
$${\hat{Y}}^p=\frac{1}{N}\sum _{i=1}^N⟨f_i^p,V^p(X_i)⟩$$

其中，$V^p(X_i)$是图像$X_i$像素$p$的$K\times K$邻域。$f_i^p$是其对应的核。在文章实验中，$K=5,N=8$。
除了RAW数据作为输入外，网络还使用逐像素估计的信号标准偏差作为输入。对噪声的逐像素估计为
$$\widehat{{\sigma }_p}=\sqrt{{\sigma }_r^2+{\sigma }_s\max (x_p,0)}$$

其中，$x_p$是图像序列中第一张图像像素$p$的亮度。假设${\sigma }_r$和${\sigma }_s$是已知的。

基本损失函数

对输出做亮度归一化，并应用sRGB变换做gamma校正。然后定义损失函数为
$$l(\hat{Y},Y^{\ast })={\lambda }_2\Vert \Gamma (\hat{Y})-\Gamma (Y^{\ast }){\Vert }_2^2+{\lambda }_1\Vert \nabla \Gamma (\hat{Y})-\nabla \Gamma (Y^{\ast }){\Vert }_1$$

其中，${\lambda }_1$和${\lambda }_2$是固定常数，文章中都设为1。$\Gamma$是sRGB变换函数：
$$\begin{gathered} \Gamma (X)=\{\begin{array}{ll}12.92X,& X\le 0.0031308\\ (1+a)X^1/2.4-a,& X>0.0031308\end{array} \\ a=0.055 \end{gathered}$$

不直接使用gamma校正函数$X^{\gamma }$是避免在$X$趋于0时其梯度趋于无穷。

退火损失项

直接优化损失函数会收敛于局部最小值（只有参考帧核非零，其余核都变为0）。为了使得网络能充分利用其它帧的信息，文章使用退火策略，在初始时刻，使得输出的核能对图像序列中的每一帧分别配准和降噪，然后再利用各帧之间的信息做加权叠加。
应用核$f_1,...,f_N$于图像帧$X_1,...,X_N$，生成N帧滤波图像$f_1(X_1),...,f_N(X_N)$，然后取平均得到输出$\hat{Y}$。对每一帧中间结果加入损失项，并在训练过程中逐渐较小，最终的随时间变化的损失函数为
$$\mathcal{L}(X;Y^{\ast },t)=l\left(\frac{1}{N}\sum _{i=1}^N{f}_i(X_i),Y^{\ast }\right)+\beta {\alpha }^t\sum _{i=1}^{N}l(f_i(X_i),Y^{\ast })$$

其中，$\beta$和$0<\alpha <1$是超参数控制退火过程，$t$是迭代次数。随着迭代次数增加，第二项逐渐减弱直至消失。在文章的实验中，$\beta =100$，$\alpha =0.9998$，需要迭代40000次才能使得第二项消失。KPN会被预先训练对每一帧图像分别配准和降噪，然后再处理整个序列。

Experiments

实验参数

优化方法：ADam；学习率：$10^{-}4$；Batch size：4；
每个图像序列大小：$129\times 128\times 8$。

比较方法

NLM、HDR+、VBM4D；
KPN（提出的方法）、
direct model（将KPN后接3个卷积层，直接输出去噪图像）；

合成测试集结果

合成测试集来自于Canon 5D Mark II DSLR拍摄的73张线性RAW数据。这些图片在白天用低ISO拍摄，使得噪声最小化，并且刻意欠曝避免截止高亮区域。将这些RAW数据每$2\times 2$Bayer块平均为一个像素，并像合成训练集一样加入偏移量和噪声，从而生成灰度图像作为输入。
实验结果

direct model倾向于输出比KPN更加平滑的结果，故其在高噪声情况下会有更好的结果，见表1（各方法在线性合成测试集上的表现，网络没有在第四列噪声水平下训练）。

表2（各方法在gamma校正后，并添加不同水平高斯白噪声的合成测试集上的表现，网络没有在第四列噪声水平下训练）

尽管网络在只有平移偏移的训练集上训练，但训练后的网络对大场景移动也有鲁棒性。

在实验过程中，一般经过前几次训练，输出的核就可以对$\pm 2$像素的偏移有很好的矫正，故设定在3-5%迭代次数后，将退火项设为0.

泛化于更高的噪声水平

在文章实验中，将噪声水平估计作为输入对网络进行训练，可以有效将网络泛化于更高的噪声水平。从下图可以看出，在训练集的噪声范围内，有无噪声水平估计作为输入对网络性能影响不大；而在训练集噪声水平之外，有噪声水平估计作为输入的网络会更有鲁棒性。

另外，输入的噪声水平估计也可以作为参数调整网络的去噪强度。从下图可以看出，当输入的噪声水平低于实际噪声水平时，网络对噪声去除比较保守，更倾向于利用参考帧的信息；当输入的噪声水平高于实际噪声水平时，网络更倾向于利用更宽的空间信息，以及多帧图像的信息，输出图像也更加平滑。

真实数据的测试结果

使用Nexus 6P在暗光场景下拍摄得到的原始数据，并只做简单的后处理如暗电流去除，抑制坏点像素，和整体配准。从结果可以看出，KPN仍能保持好的性能。

代码地址：GitHub地址（好像只有网络训练的代码）