【p3128、LQB14I砍树】树上差分

本文主要是介绍【p3128、LQB14I砍树】树上差分，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

差分

差分数组求法：
设原始数组是arr，差分数组是b

• b[0] = arr[0];
• b[i] = arr[i] - arr[i-1];

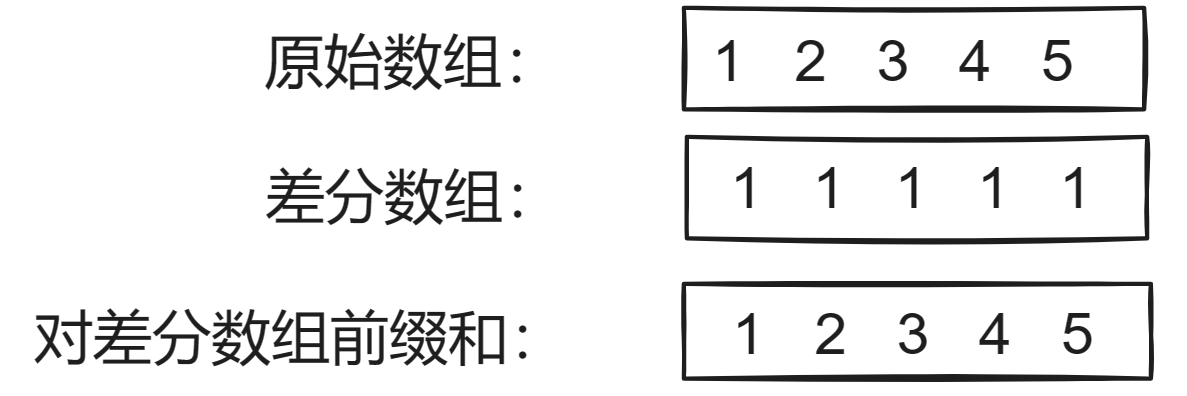
如果我们要对图中2-4区间的数每个都加上3，就可以在差分数组2的位置加上3，在差分数组4的后一个元素即5的位置减去一个3（目的是消除3对后面区间的影响），再对差分数组前缀和即可完成。

树上差分

多次对树上路径做加法操作，然后询问对某个点操作后的值，适用树上差分。

差分数组求法：

• 叶子节点的差分值是叶子节点的权重
• 其他节点的差分值是权-子权和

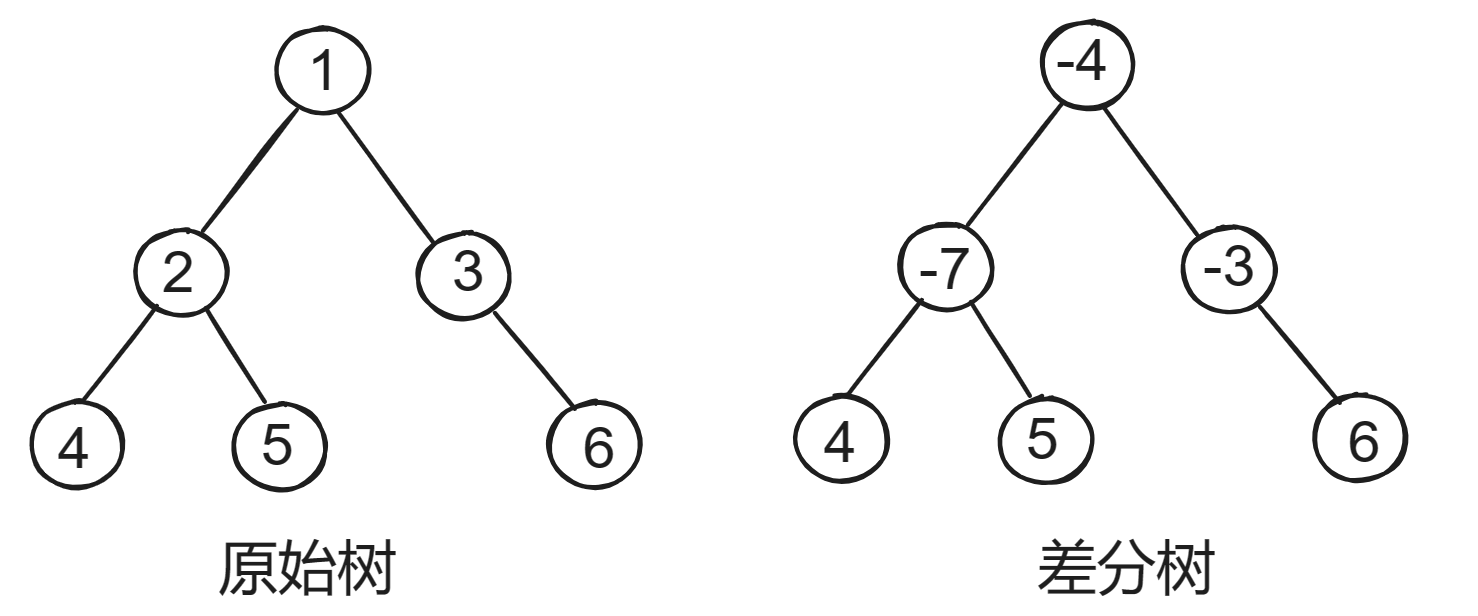
• 权 = 差分值 + 子权和

p3128

LQB14I砍树

题目

题目信息：
给定一棵由 n 个结点组成的树以及 m 个不重复的无序数对 (a1, b1), (a2, b2),
. . . , (am, bm)，其中 ai 互不相同，bi 互不相同，ai ≠ bj(1 ≤ i, j ≤ m)。
小明想知道是否能够选择一条树上的边砍断，使得对于每个 (ai , bi) 满足 ai和 bi 不连通，如果可以则输出应该断掉的边的编号（编号按输入顺序从 1 开始），否则输出 -1.

输入输出：
输入共 n + m 行，第一行为两个正整数 n，m。
后面 n − 1 行，每行两个正整数 xi，yi 表示第 i 条边的两个端点。
后面 m 行，每行两个正整数 ai，bi。

一行一个整数，表示答案，如有多个答案，输出编号最大的一个。

输入：
6 2
1 2
2 3
4 3
2 5
6 5
3 6
4 5
4

输出：
4

解题步骤

1. 要使砍掉一条边后每一数对都不连通，就要让所有数对都经过这条边。
2. 将边权下移到点上，对x和y两点间的操作变为：s[x]++;s[y]++;s[LCA(x,y)]-=2;(其中s是差分数组)。
3. 操作完成后，如果有边的权值恰好等于m，更新答案。

代码样例

#include <bits/stdc++.h>
using namespace std;const int N = 1e5+5;int n,m,dep[N],fa[N][21],ans,s[N];vector<int> e[N],num[N];void dfs(int u,int father){dep[u] = dep[father] + 1;fa[u][0] = father;for(int i = 1;i<=20;i++){fa[u][i] = fa[fa[u][i-1]][i-1];}for(int i = 0;i<e[u].size();i++){int v = e[u][i];if(v == father) continue;dfs(v,u);}
}int LCA(int u,int v)
{if(dep[u] < dep[v]) swap(u,v);for(int i = 20;i>=0;i--){if(dep[fa[u][i]] >= dep[v]) u = fa[u][i];}if(u == v) return u;for(int i = 20;i>=0;i--){if(fa[u][i] != fa[v][i]) u = fa[u][i] , v=fa[v][i];}return fa[u][0];
}void dfs2(int u,int Fa)
{for(int i = 0;i<e[u].size();i++){int v = e[u][i], p = num[u][i];if(v == Fa) continue;dfs2(v,u);s[u] += s[v];if(s[v] == m) ans=max(ans,p);}
//	if(s[u] == m) ans=max(ans,p);
} int main()
{cin >> n >> m;for(int i = 1;i<n;i++){int x,y;cin >> x >> y;e[x].push_back(y);e[y].push_back(x);num[x].push_back(i);num[y].push_back(i);}	dfs(1,0);	//差分for(int i = 1;i<=m;i++){int a,b;cin >> a >> b;s[a]++;s[b]++;s[LCA(a,b)]-=2;} //统计结果 dfs2(1,0);cout << ans << endl;return 0;
}

这篇关于【p3128、LQB14I砍树】树上差分的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---