掘根宝典之C语言原码，反码，补码，位操作运算符（~,,|,^,＜＜,＞＞,=,|=,^=,＞＞=,＜＜=）

2024-03-06 13:28
文章标签 语言 运算符 宝典 原码 位操作 反码 补码 掘根

本文主要是介绍掘根宝典之C语言原码，反码，补码，位操作运算符（~,,|,^,＜＜,＞＞,=,|=,^=,＞＞=,＜＜=），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

目录

二进制数

什么是二进制数

c语言中的二进制数

机器数

原码

正数计算

负数计算

反码

负数计算

跨零计算

补码

定义

跨零计算

总结

按位逻辑运算符（~，&，&=,|，|=，^，^=）

按位取反：~

按位与：&和&=

按位或：|和|=

按位异或：^

用法

掩码

打开位(设置位）

关闭位（清空位）

切换位

检查位的值

移位运算符（<<，<<=，>>，>>=）

左移：<<和<<=

右移：>>和>>=

用法：移位运算符

二进制数

什么是二进制数

二进制数是一种数值系统，它只使用两个数字0和1来表示数值。在计算机科学和数字电子技术中，二进制数被广泛使用来表示和处理信息。

与我们平常使用的十进制数系统不同，二进制数系统基于2的幂次方。每个二进制位（或称为二进制位或比特）可以代表0或1。从右往左，每个位的权值是2的幂次方递增，从0开始。

例如，下面是一个8位二进制数的示例：

  1    0    1    0    1    0    1    0
2^7  2^6  2^5  2^4  2^3  2^2  2^1  2^0

将每个位与其对应的幂次方的乘积相加，可以得到该二进制数对应的十进制数。例如，上述二进制数的值为：

(1 * 2^7) + (0 * 2^6) + (1 * 2^5) + (0 * 2^4) + (1 * 2^3) + (0 * 2^2) + (1 * 2^1) + (0 * 2^0) = 170

二进制数在计算机编程中非常重要，因为计算机处理和存储数据的最基本单位是位。所有的数据和指令在计算机内部都以二进制的形式进行处理和表示。因此，理解和使用二进制数是计算机编程的基础之一。

c语言中的二进制数

C语言中表示二进制数的方法有很多种。下面列举了一些常用的方法：

  1. 使用二进制字面量表示：可以在数字前面加上0b或0B前缀表示该数字是二进制数。例如，int binary = 0b101010;表示二进制数101010。

  2. 使用位运算符表示：可以使用位运算符来手动构建二进制数。例如，int binary = (1 &lt;&lt; 5) | (1 &lt;&lt; 3) | (1 &lt;&lt; 1);表示二进制数101010。

  3. 使用字符串表示：可以使用字符串来表示二进制数，然后使用相应的函数将其转换为二进制数。例如，const char* binaryStr = "101010"; int binary = strtol(binaryStr, NULL, 2);表示二进制数101010。

无论使用哪种方法，C语言中的二进制数最终都会被存储为二进制位的形式。在内存中，整数类型会以二进制位的形式存储，并根据数据类型的不同分配不同的字节数。在程序中，可以使用位运算符来对二进制数进行位操作，比如与、或、非等操作。

机器数

一个数在计算机中的表示形式是二进制的话，这个数其实就叫机器数。

机器数通常是带有符号的（指有正数和负数之分），计算机用最高位存放符号，这个 bit 一般叫做符号位。 正数的符号位为 0， 负数的符号位为 1。

比如，十进制中的数 +7 ，计算机字长为8位，转换成二进制就是 0 0 0 0 0 1 1 1（一个 byte 有 8bit，有效的取值范围是 -128 ~ +127）。

如果是 -7 ，就是 1 0 0 0 0 1 1 1 。一个存储的二进制码分原码、反码、补码，下面我们就来介绍一下什么是原码、反码、补码

原码

定义

十进制数据的二进制表现形式就是原码，原码最左边的一个数字就是符号位，0为正，1为负。

例如：56 -> 0 0 1 1 1 0 0 0

左边第一位为符号位，其他位为数据位。

一个 byte 有 8bit，最大值是 0 1 1 1 1 1 1 1 (+127)，最小值是 1 1 1 1 1 1 1 1 (-128)

在计算机中之所以使用二进制来表示原码是因为逻辑简单，对于电路来说只有开或者关两种状态，用二进制是在方便不过的了。如果使用的进制是十进制、八进制或者十六进制的话，电路没有办法表示那么多的状态

正数计算


使用原码对正数进行计算不会有任何问题的

例如：5 + 2

 0 0 0 0 0 1 0 1
+        0 0 1 0
-----------------0 0 0 0 0 1 1 1



把这个结果转成十进制刚好就等于 7，完全正确无误

负数计算


但是如果是负数的话，那计算的结果就会大相径庭了

我们拿 -56 这个数字来举例，它的原码是 1 0 1 1 1 0 0 0 ，减一之后，就会变成 1 0 1 1 0 1 1 1 ，这个数转成十进制就是 -55。计算前是 -56，减一之后正确的结果应该是 -57（1 0 1 1 1 0 0 1）才对，居然还越减越大了

 1 0 1 1 1 0 0 0
-              1
-----------------1 0 1 1 0 1 1 1


为了解决原码不能用于计算负数的这种问题，这时候，反码它出现了，作为负数的“计算的救星”。

计算规则是正数的反码不变和原码一致，负数的反码会在原码的基础上，高位的符号位不变，其他位取反（ 1 变成 0 ， 0 变为 1 ）。

反码


定义

正数的反码是其本身（等于原码），负数的反码是符号位保持不变，其余位取反。

反码的存在是为了正确计算负数，因为原码不能用于计算负数

十进制数字    原码    反码
+0    0000 0000    0000 0000
-0    1000 0000    1111 1111
-1    1000 0001    1111 1110
-2    1000 0010    1111 1101
-3    1000 0011    1111 1100
-4    1000 0100    1111 1011
-5    1000 0101    1111 1010
-6    1000 0110    1111 1001
-7    1000 0111    1111 1000


负数计算


这时候，我们再来使用反码计算一下 -56 - 1 的结果

-56 的原码是 1 0 1 1 1 0 0 0 ，如果转成反码（符号位不变，其他位取反），

那么它的反码就是 1 1 0 0 0 1 1 1

  1 1 0 0 0 1 1 1-              1
-----------------1 1 0 0 0 1 1 0


-56 -1 = -57，-57 的原码是 1 0 1 1 1 0 0 1，转成反码刚好是 1 1 0 0 0 1 1 0，刚好等于刚才我们算出的值

跨零计算


不过反码也有它的 “ 软肋 ”，如果是负数跨零进行计算的话，计算得出的结果不对

我们拿 -3 + 5 来举例

-3 的原码是 1 0 0 0 0 0 1 1，转成反码的话就是 1 1 1 1 1 1 0 0

 1 1 1 1 1 1 0 0
+        0 1 0 1  
-----------------0 0 0 0 0 0 0 1 


把计算结果转成十进制就是 1，这结果显然不对。那么我们该怎么计算呢，这时候，作为反码的补充编码 —— 补码就出现了。

补码


定义

正数的补码是其本身，负数的补码等于其反码 +1。

因为反码不能解决负数跨零（类似于 -6 + 7）的问题，所以补码出现了。

十进制数字    原码    反码    补码
+0    0000 0000    0000 0000    0000 0000
-0    1000 0000    1111 1111    0000 0000
-1    1000 0001    1111 1110    1111 1111
-2    1000 0010    1111 1101    1111 1110
-3    1000 0011    1111 1100    1111 1101
-4    1000 0100    1111 1011    1111 1100
-5    1000 0101    1111 1010    1111 1011
-6    1000 0110    1111 1001    1111 1010
-7    1000 0111    1111 1000    1111 1001
…    …    …    …
-127    1111 1111    1000 0000    1000 0001
-128    无    无    1000 0000


跨零计算


这时候，我们再来使用反码计算一下 -3 + 5 的结果

-3 的原码是 1 0 0 0 0 0 1 1，转成反码的话就是 1 1 1 1 1 1 0 0，再转成补码就是 1 1 1 1 1 1 0 1

 1 1 1 1 1 1 0 1
+        0 1 0 1
----------------- 0 0 0 0 0 0 1 0

把这个数转成十进制刚好等于2，结果正确

总结


在计算机当中都是使用补码来进行计算和存储的。补码很好的解决了反码负数不能跨零计算的弊端，并且补码还可以记录一个特殊的值 -128，这个数据在 1 个字节下是没有原码和反码

按位逻辑运算符（~，&，&=,|，|=，^，^=）

按位取反：~

一元运算符～把1变为0，把0变为1。

如下例子所示：

~(10011010) // 表达式
(01100101) //结果值


假设val的类型是unsigned char，已被赋值为2。在二进制中，00000010表示2。那么，～yal的值是11111101，即253。

注意，该运算符不会改变val的值，就像3*val不会改变val的值一样，ral仍然是2。

但是，该运算符确实创建了一个可以使用或赋值的新值：

newval = ~val;
printf("%d",~val);


如果要把val的值改为～val，使用下面这条语句：

val =~val;


按位与：&和&=


二元运算符通过逐位比较两个运算对象，生成一个新值。

对于每个位，只有两个运算对象中相应的位都为1时，结果才为1

(从真/假方面看，只有当两个位都为真时，结果才为真)。

因此，对下面的表达式求值：

(10010011) & (00111101) // 表达式

由于两个运算对象中编号为4和0的位都为1，得：

(00010001) // 结果值


C有一个按位与和赋值结合的运算符:&=。

下面两条语句产生的最终结果相同：

val &= 0377;
val= val & 0377;


按位或：|和|=


二元运算符1，通过逐位比较两个运算对象，生成一个新值。

对于每个位，如果两个运算对象中相应的位为1，结果就为1

(从真/假方面看，如果两个运算对象中相应的一个位为真或两个位都为真，那么结为真)。

因此，对下面的表达式求值：

(00111101) //表达式
(10010011)1


除了编号为6的位，这两个运算对象的其他位至少有一个位为1，得：

(10111111)// 结果值


c有一个按位或和赋值结合的运算符：|=。

下面两条语句产生的最终作用相同：

val |= 0377;
val =val | 0377;

按位异或：^

二元运算符^逐位比较两个运算对象。

对于每个位，如果两个运算对象中相应的位一个为1(但不是两个为1)，结果为1

(从真/假方面看，如果两个运算对象中相应的一个位为真且不是两个为同为1，那么结果为真）。

果为真)。

因此，对下面表达式求值：
 

(00111101)^(10010011)//表达式


编号为0的位都是1，所以结果为0，得：

(10101110) //结果值


有一个按位异或和赋值结合的运算符：=。

下面两条语句产生的最终作用相同：
 

val ^= 0377;
val=val ^ 0377;

用法

掩码


按位与运算符常用于掩码(mask)。所谓掩码指的是一些设置为开(1)或关(O)的位组合。要明白来其为掩码的原因，先来看通过6把一个量与掩码结合后发生什么情况。

例如，假设定义符号常量238为2(即，二进制形式为00000010)，只有1号位是1，其他位都是0。下面的语句：
 

flags = flags & MASK;


把flags中除1号位以外的所有位都设置为0，因为使用按位与运算符(g)任何位与0组合都得0。1号位的值不变(如果1号位是1，那么1&1得1；如果1号位是0，那么0&1也得0)。这个过程叫作“使用掩码”，因为掩码中的0隐藏了flags中相应的位。
可以这样类比：把掩码中的0看作不透明，1看作透明。

表达式flags & MASK相当于用掩码覆盖在flags的位组合上，只有MASK为1的位才可见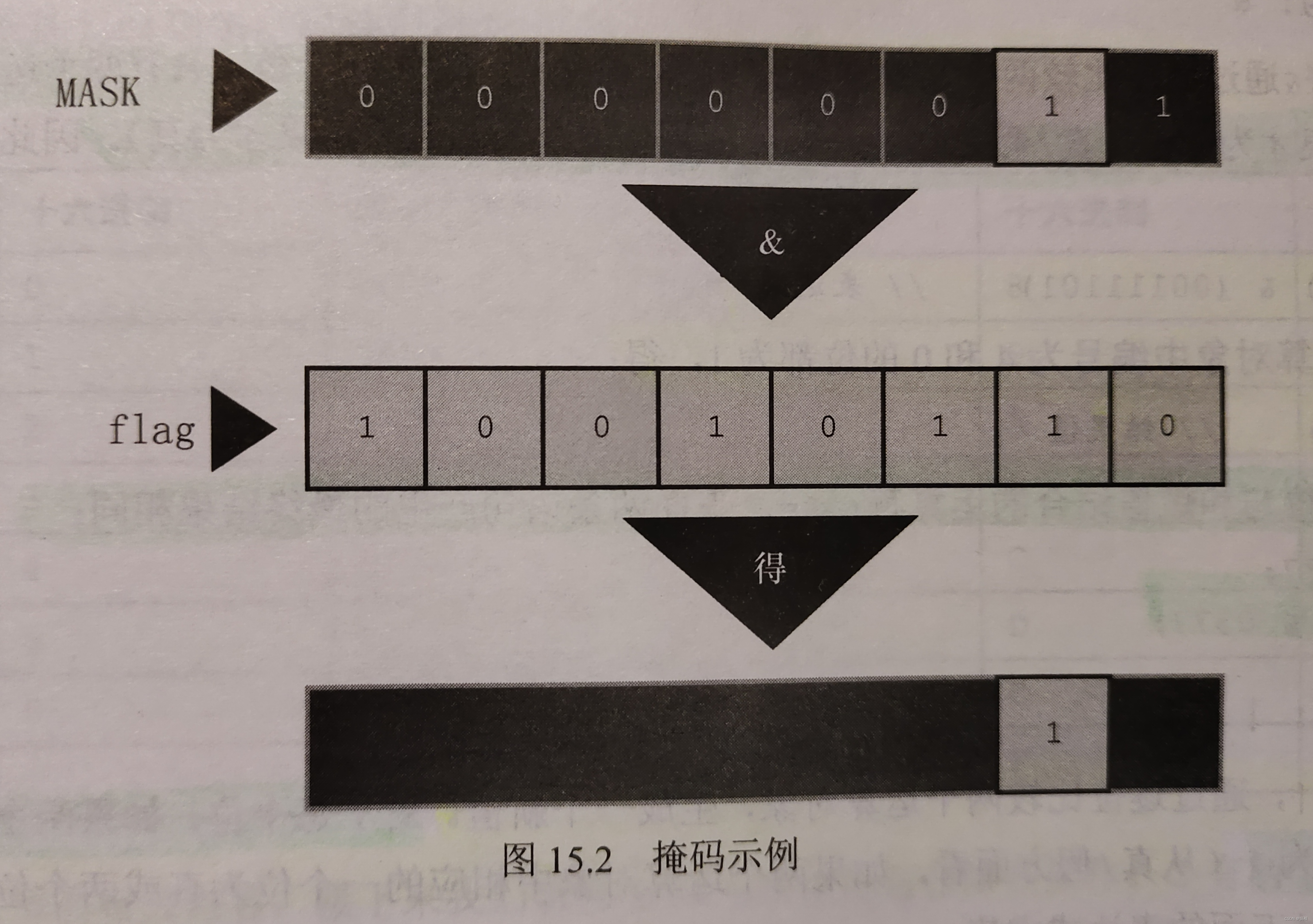


用&=运算符可以简化前面的代码，如下所示：
 

flags &= MASK;


下面这条语句是按位与的一种常见用法：
 

ch &= 0xff；/*或者 ch &= 0377；*/


oxff的二进制形式是11111111，八进制形式是0377。

这个掩码保持ch中最后8位不变，其他位都设置为0。无论ch原来是8位、16位或是其他更多位，最终的值都被修改为1个8位字节。在该例中，掩码的宽度为8位。
 

打开位(设置位）


有时，需要打开一个值中的特定位，同时保持其他位不变。

例如，一台IBM PC通过向端口发送值来控制硬件。例如，为了打开内置扬声器，必须打开1号位，同时保持其他位不变。

这种情况可以使用校位或运算符(|)。
 

以上一节的flags和MASK(只有1号位为1)为例。下面的语句：
 

flags =flags | MASK;


把flags的1号位设置为1，且其他位不变。

因为使用|运算符，任何位与0组合，结果都为本身；任何位与1组合，结果都为1。
 

例如，假设flags是00001111，MASK是10110110。下面的表达式：
 

flags | MASK
即是：
(00001111）|(10110110) // 表达式
其结果为：
(10111111) // 结果值


MASK中为1的位，flags与其对应的位也为1。MASK中为0的位，flags与其对应的位不变。

用|=运算符可以简化上面的代码，如下所示：
 

flags |= MASK;


同样，这种方法根据MASK中为1的位，把flags中对应的位设置为1，其他位不变。


关闭位（清空位）


和打开特定的位类似，有时也需要在不影响其他位的情况下关闭指定的位。

假设要关闭变量flags中的1号位。同样，MASK只有1号位为1(即，打开)。

可以这样做：
 

flags = flags & ~MASK;


由于MASK除1号位为1以外，其他位全为0，所以～MASK除1号位为0以外，其他位全为1。

使用&，任何位与1组合都得本身，所以这条语句保持1号位不变，改变其他各位。

另外，使用&，任何位与0组合都得0。所以无论1号位的初始值是什么，都将其设置为0。
 

例如，假设f1ags是00001111，MASK是10110110。下面的表达式：

flags &~MASK
即是：
(00001111）&~(10110110) // 表达式
其结果为：
(00001001) // 结果值


MASK中为1的位在结果中都被设置(清空)为0。flags中与MASK为0的位相应的位在结果中部改变。
可以使用下面的简化形式：
 

 flags &=~MASK;

切换位


切换位指的是打开已关闭的位，或关闭已打开的位。

可以使用按位异或运算符(^)切换位。

也就是说，假设b是一个位(1或0)，如果b为1，则1^b为0；如果b为0，则1b为1。

另外，无论b为1还是0，0^b均为b。

因此，如果使用^组合一个值和一个掩码，将切换该值与MASK为1的位相对应的位，该值与MASR为0的位相对应的位不变。

要切换flags中的1号位，可以使用下面两种方法：
 

flags = flags^ MASK;
flags^= MASK;


例如，假设flags是00001111，MASK是10110110。表达式：
 

flags^NASK
即是：
(00001111) (10110110) // 表达式
其结果为：
(10111001) // 结果值


flags中与MASK为1的位相对应的位都被切换了，MASK为0的位相对应的位不变。
 

检查位的值


前面介绍了如何改变位的值。有时，需要检查某位的值。

例如，flags中1号位是否被设置为1?不能这样直接比较flags 和MASK:
 

if(flags == MASK)
puts("Wow!")；/*不能正常工作*/


这样做即使flags的1号位为1，其他位的值会导致比较结果为假。因为其他位的值会导致比较结果为假。

因此，必须覆盖f1ags中的其他位，只用1号位和MASK比较：
 

if ((flags & MASK) == MASK)
puts("Wow!");


由于按位运算符的优先级比==低，所以必须在flags & MASK周围加上圆括号。
为了避免信息漏过边界，掩码至少要与其覆盖的值宽度相同。
 

移位运算符（<<，<<=，>>，>>=）


下面介绍C的移位运算符。移位运算符向左或向右移动位。


左移：<<和<<=


左移运算符(<<)将其左侧运算对象每一位的值向左移动其右侧运算对象指定的位数。

左侧运算对象移出左末端位的值丢失，用0填充空出的位置。

下面的例子中，每一位都向左移动两个位置：
 

(10001010)<<2// 表达式
(00101000） // 结果值


该操作产生了一个新的位值，但是不改变其运算对象。例如，假设stonk为1， tonk<<2为4，但是stonk本身不变，仍为1。可以使用左移赋值运算符(<<=)来更改。

该运算符将变量中的位向左移动其右侧运算对象给定值的位数。如下例：
 

int onkoo;
int stonk=1;
onkoo = stonk << 2;/*把4赋给onkoo*/
stonk <<= 2;  /*把stonk的值改为4*/


右移：>>和>>=


右移运算符(>>)将其左侧运算对象每一位的值向右移动其右侧运算对象指定的位数。

左侧运算对象移出右末端位的值丢。

对于无符号类型，用0填充空出的位置。

(10001010)>> 2 // 表达式，无符号值
(00100010) // 所有系统都得到该结果值


每个位向右移动两个位置，空出的位用0填充。

对于有符号类型，其结果取决于机器，空出的位置可用0填充，或者用符号位(即，最左端的位)的副本填充。
 

(10001010)>> 2 /1表达式，有符号值
(00100010) 在某些系统中的结果值
(10001010）>> 2 /1表达式，有符号值
(11100010) /1 在另一些系统上的结果值



右移赋值运算符(>>=)将其左侧的变量向右移动指定数量的位数。

如下所示：
 

int sweet = 16;
int ooosw;
ooosw = sweet >> 3; // ooosw = 2, sweet的值仍然为16
sweet >>=3; // sweet的值为2


用法：移位运算符


移位运算符针对2的幂提供快速有效的乘法和除法：
 

number乘以2的n次幂
number << n
如果number 为非负，则用number除以2的n次幂
number >> n


这些移位运算符类似于在十进制中移动小数点来乘以或除以10。


移位运算符还可用于从较大单元中提取一些位。

例如，假设用一个unsigned 1ong类型的值表示值，低阶位字节储存红色的强度，下一个字节储存绿色的强度，第3个字节储存蓝色的强度。

随后把每种颜色的强度分别储存在3个不同的unsigned char类型的变量中。

那么，可以使用下面的语句
 

#define BYTE_MASK Oxff
unsigned long color= 0x002a162f;
unsigned char blue, green, red;
red=color&BYTE_MASK;
green=(color>>8)& BYTE_MASK;
blue=(color>>16) & BYTE MASK;


右移运算符将8位颜色值移动至低阶字节，然后使用掩码技术把低阶字节，然后使用掩码技术把低阶字节赋给指定的变量
 

这篇关于掘根宝典之C语言原码，反码，补码，位操作运算符（~,,|,^,＜＜,＞＞,=,|=,^=,＞＞=,＜＜=）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/780196。

相关文章

C语言中的数据类型强制转换

C语言中的数据类型强制转换

《C语言中的数据类型强制转换》：本文主要介绍C语言中的数据类型强制转换方式,具有很好的参考价值,希望对大家有所帮助,如有错误或未考虑完全的地方,望不吝赐教... 目录C语言数据类型强制转换自动转换强制转换类型总结C语言数据类型强制转换强制类型转换：是通过类型转换运算来实现的，主要的数据类型转换分为自动转换
阅读更多...
利用Go语言开发文件操作工具轻松处理所有文件

利用Go语言开发文件操作工具轻松处理所有文件

《利用Go语言开发文件操作工具轻松处理所有文件》在后端开发中,文件操作是一个非常常见但又容易出错的场景,本文小编要向大家介绍一个强大的Go语言文件操作工具库,它能帮你轻松处理各种文件操作场景... 目录为什么需要这个工具？核心功能详解1. 文件/目录存javascript在性检查2. 批量创建目录3. 文件
阅读更多...
C语言实现两个变量值交换的三种方式

C语言实现两个变量值交换的三种方式

《C语言实现两个变量值交换的三种方式》两个变量值的交换是编程中最常见的问题之一,以下将介绍三种变量的交换方式,其中第一种方式是最常用也是最实用的,后两种方式一般只在特殊限制下使用,需要的朋友可以参考下... 目录1.使用临时变量（推荐）2.相加和相减的方式（值较大时可能丢失数据）3.按位异或运算1.使用临时
阅读更多...
使用C语言实现交换整数的奇数位和偶数位

使用C语言实现交换整数的奇数位和偶数位

《使用C语言实现交换整数的奇数位和偶数位》在C语言中,要交换一个整数的二进制位中的奇数位和偶数位,重点需要理解位操作,当我们谈论二进制位的奇数位和偶数位时,我们是指从右到左数的位置,本文给大家介绍了使... 目录一、问题描述二、解决思路三、函数实现四、宏实现五、总结一、问题描述使用C语言代码实现：将一个整
阅读更多...
C语言字符函数和字符串函数示例详解

C语言字符函数和字符串函数示例详解

《C语言字符函数和字符串函数示例详解》本文详细介绍了C语言中字符分类函数、字符转换函数及字符串操作函数的使用方法,并通过示例代码展示了如何实现这些功能,通过这些内容,读者可以深入理解并掌握C语言中的字... 目录一、字符分类函数二、字符转换函数三、strlen的使用和模拟实现3.1strlen函数3.2st
阅读更多...
Go语言中最便捷的http请求包resty的使用详解

Go语言中最便捷的http请求包resty的使用详解

《Go语言中最便捷的http请求包resty的使用详解》go语言虽然自身就有net/http包,但是说实话用起来没那么好用,resty包是go语言中一个非常受欢迎的http请求处理包,下面我们一起来学... 目录安装一、一个简单的get二、带查询参数三、设置请求头、body四、设置表单数据五、处理响应六、超
阅读更多...
C语言中的浮点数存储详解

C语言中的浮点数存储详解

《C语言中的浮点数存储详解》：本文主要介绍C语言中的浮点数存储详解,具有很好的参考价值,希望对大家有所帮助,如有错误或未考虑完全的地方,望不吝赐教... 目录1、首先明确一个概念2、接下来，讲解C语言中浮点型数存储的规则2.1、可以将上述公式分为两部分来看2.2、问：十进制小数0.5该如何存储？2.3 浮点
阅读更多...
Java逻辑运算符之&&、|| 与&、 |的区别及应用

Java逻辑运算符之&&、|| 与&、 |的区别及应用

《Java逻辑运算符之&&、||与&、|的区别及应用》：本文主要介绍Java逻辑运算符之&&、||与&、|的区别及应用的相关资料,分别是&&、||与&、|,并探讨了它们在不同应用场景中... 目录前言一、基本概念与运算符介绍二、短路与与非短路与：&& 与 & 的区别1. &&：短路与（AND）2. &：非短
阅读更多...
基于Python实现多语言朗读与单词选择测验

基于Python实现多语言朗读与单词选择测验

《基于Python实现多语言朗读与单词选择测验》在数字化教育日益普及的今天,开发一款能够支持多语言朗读和单词选择测验的程序,对于语言学习者来说无疑是一个巨大的福音,下面我们就来用Python实现一个这... 目录一、项目概述二、环境准备三、实现朗读功能四、实现单词选择测验五、创建图形用户界面六、运行程序七、
阅读更多...
使用Go语言开发一个命令行文件管理工具

使用Go语言开发一个命令行文件管理工具

《使用Go语言开发一个命令行文件管理工具》这篇文章主要为大家详细介绍了如何使用Go语言开发一款命令行文件管理工具,支持批量重命名,删除,创建,移动文件,需要的小伙伴可以了解下... 目录一、工具功能一览二、核心代码解析1. 主程序结构2. 批量重命名3. 批量删除4. 创建文件/目录5. 批量移动三、如何安
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2