本文主要是介绍力扣543. 二叉树的直径,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
Problem: 543. 二叉树的直径
文章目录
- 题目描述
- 思路
- 复杂度
- Code
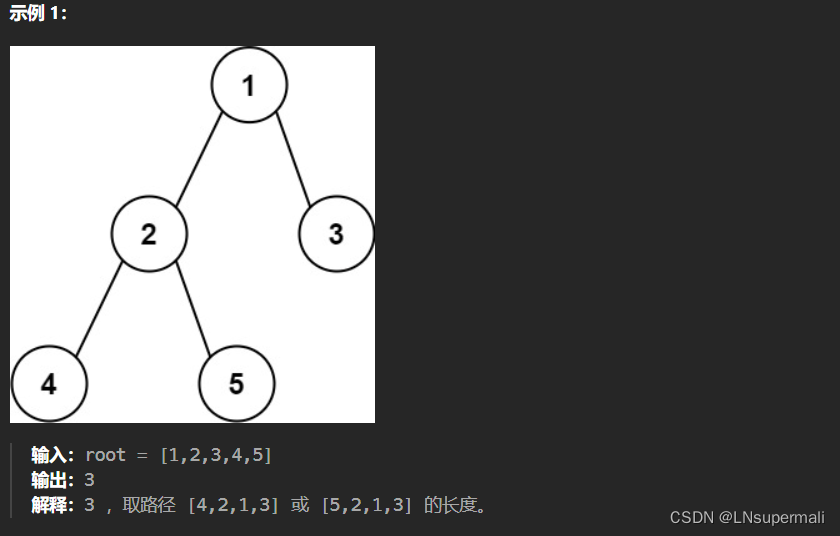
题目描述
思路
1.最大直径 == 左子树的最大深度 + 右子树的最大深度;
2.定义一个变量maxDiameter记录最大直径,并编写一个递归函数maxDepth,利用树的后序遍历每次递归求取leftMax(左子树的最大深度)和rightMax(右子树的最大深度),同时更新maxDiameter(maxDiameter == max(maxDiameter, (leftMax + rightMax)));递归函数每次返回1 + max(leftMax, rightMax)
复杂度
时间复杂度:
O ( n ) O(n) O(n);其中 n n n为数的节点个数
空间复杂度:
O ( h ) O(h) O(h);其中 h h h为树的高度
Code
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {//Maximum recorded diameterint maxDiameter = 0;
public:/***Find the maximum diameter** @param root The root of binary tree* @return int*/int diameterOfBinaryTree(TreeNode* root) {maxDepth(root);return maxDiameter;}/*** Post-order traversal** @param root The root of binary tree* @return int*/int maxDepth(TreeNode* root) {if (root == nullptr) {return 0;}int leftMax = maxDepth(root -> left);int rightMax = maxDepth(root -> right);//After the order position, find the maximum diameterint myDiameter = leftMax + rightMax;maxDiameter = max(myDiameter, maxDiameter);return 1 + max(leftMax, rightMax);}
};
这篇关于力扣543. 二叉树的直径的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!