Leetcode 850. 矩形面积 II

1.题目描述

我们给出了一个（轴对齐的）二维矩形列表 rectangles 。 对于 rectangle[i] = [x1, y1, x2, y2]，其中（x1，y1）是矩形 i 左下角的坐标，$ (x_{i1}, y_{i1})$ 是该矩形 左下角 的坐标，$ (x_{i2}, y_{i2}) $是该矩形 右上角 的坐标。

计算平面中所有 rectangles 所覆盖的 总面积 。任何被两个或多个矩形覆盖的区域应只计算 一次 。

返回 总面积 。因为答案可能太大，返回 $10^9+7$ 的 模 。

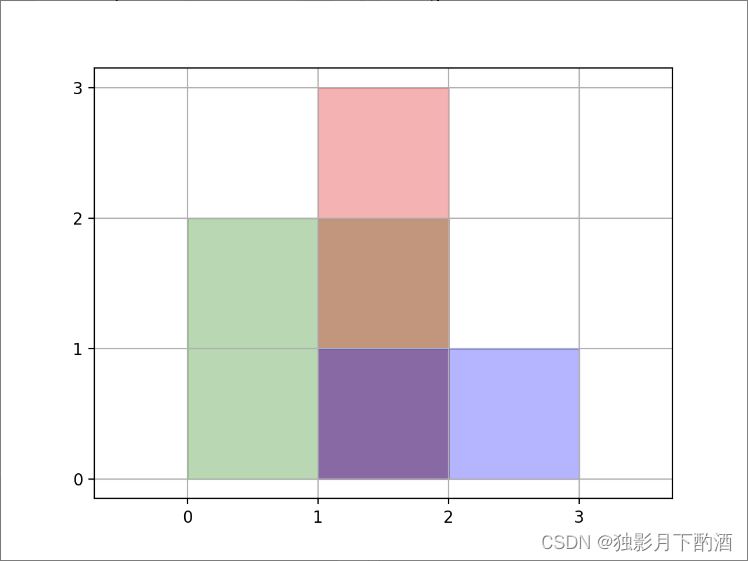
输入：rectangles = [[0,0,2,2],[1,0,2,3],[1,0,3,1]]
输出：6
解释：如图所示，三个矩形覆盖了总面积为6的区域。
从(1,1)到(2,2)，绿色矩形和红色矩形重叠。
从(1,0)到(2,3)，三个矩形都重叠。

输入：rectangles = [[0,0,1000000000,1000000000]]
输出：49
解释：答案是 $10^{18}$ 对 $(10^9+7)$ 取模的结果， 即 49 。

提示：

• 1 <= rectangles.length <= 200
• rectanges[i].length = 4
• $0<=x_{i1},y_{i1},x_{i2},y_{i2}<=10^9$
• 矩形叠加覆盖后的总面积不会超越 $2^{63}-1$ ，这意味着可以用一个 64 位有符号整数来保存面积结果。

2.思路分析

离散化+扫描线+线段树

Q1: 什么是扫描线？

扫描线就是用来解决矩形覆盖面积问题。

假如想要计算下图的覆盖面积，需要计算两个矩形的面积相加，然后减去中间蓝色交叉的部分。

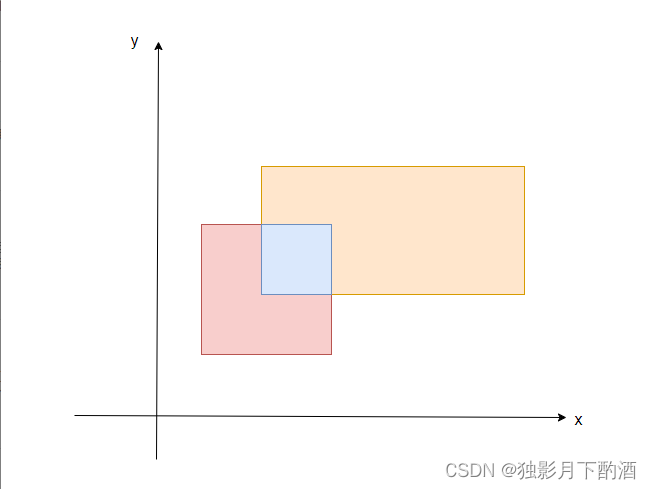
若有n个矩形，需要计算n个矩形的面积相加计算，然后减去两两交叉的面积，时间复杂度非常高。

假如可以对其进行分割，如图：

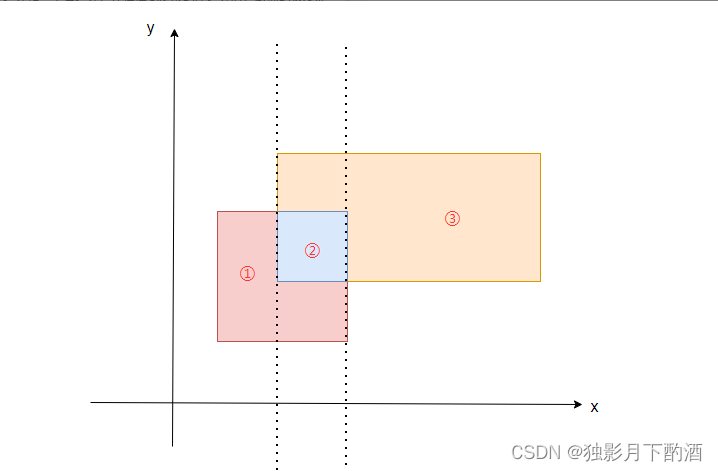
只需要计算矩形①②③的面积即可，于是问题转化为如何计算矩形①②③的面积。

矩形的宽的计算，只需要把x轴的点按照从小到大的顺序排列即可。

难点是计算矩形的高。于是便有了扫描线。

定义：从左向右看，定义矩形的左侧边为入边，右侧边为出边，也就是扫描的方向，看起来就像用一个线从左向右来扫描所有的矩形

从左往右扫，遇到入边的线，则对入边区间进行+1操作，遇到出边的线，那么对出边区间进行-1操作。然后我们遍历整个区间，就得到了矩形的高。

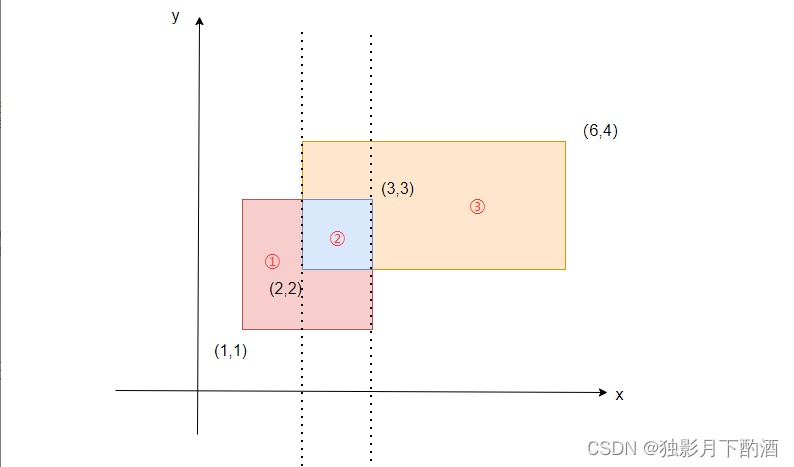
• 当扫描到第一条边，是入边，范围是[1,3]，于是给[1,3] + 1，此时整个范围只有[1,3]被覆盖，高为2，第一个矩形面积为 1 * 2 = 2

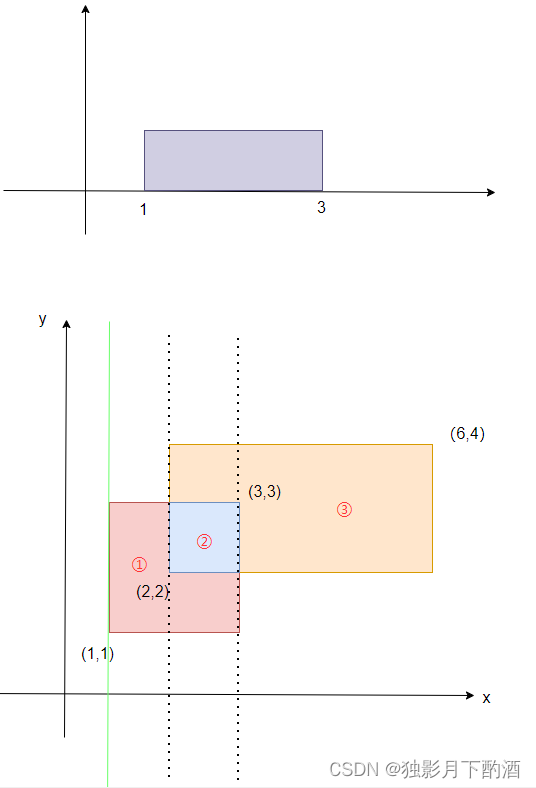
• 当扫描到第二条边，是入边，范围是[2,4]，于是给[2,4] + 1，此时整个范围只有[1,4]被覆盖，高为3，第一个矩形面积为 1 * 3 = 3

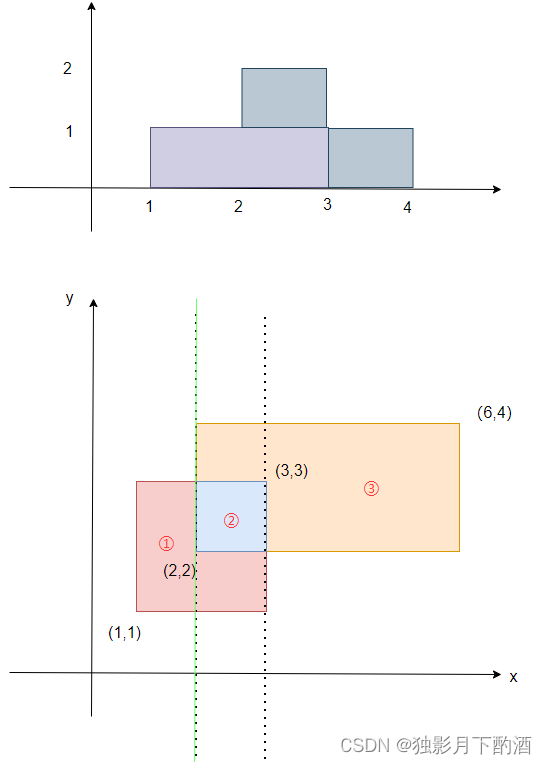
• 当扫描到第三条边，是出边，范围是[1,3]，于是给[1,3] - 1，此时整个范围只有[2,4]被覆盖，高为2，第一个矩形面积为 3 * 2 = 6

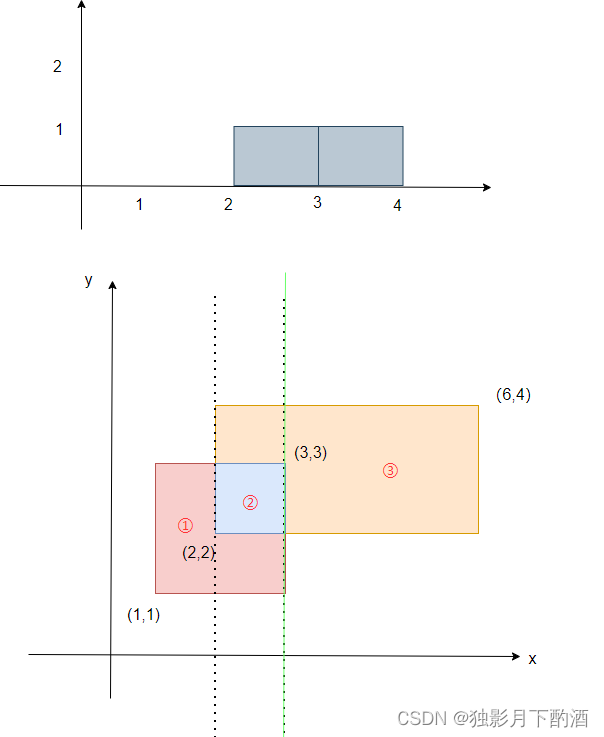
• 当扫描到第四条边，是出边，范围是[2,4]，于是我们给[2,4] - 1，此时整个范围没有覆盖，结束计算

于是覆盖面积为2 + 3 + 6 = 11

3.代码实现

class Solution:def rectangleArea(self, rectangles: List[List[int]]) -> int:hbound = set()for rect in rectangles:# 下边界hbound.add(rect[1])# 上边界hbound.add(rect[3])hbound = sorted(hbound)m = len(hbound)# 「思路与算法部分」的 length 数组并不需要显式地存储下来# length[i] 可以通过 hbound[i+1] - hbound[i] 得到seg = [0] * (m - 1)sweep = list()for i, rect in enumerate(rectangles):# 左边界sweep.append((rect[0], i, 1))# 右边界sweep.append((rect[2], i, -1))sweep.sort()ans = i = 0while i < len(sweep):j = iwhile j + 1 < len(sweep) and sweep[i][0] == sweep[j + 1][0]:j += 1if j + 1 == len(sweep):break# 一次性地处理掉一批横坐标相同的左右边界for k in range(i, j + 1):_, idx, diff = sweep[k]left, right = rectangles[idx][1], rectangles[idx][3]for x in range(m - 1):if left <= hbound[x] and hbound[x + 1] <= right:seg[x] += diffcover = 0for k in range(m - 1):if seg[k] > 0:cover += (hbound[k + 1] - hbound[k])ans += cover * (sweep[j + 1][0] - sweep[j][0])i = j + 1return ans % (10**9 + 7)

复杂度分析:

• 时间复杂度:$O(n^2)$, 其中 n 是矩形的个数。
• 空间复杂度:$O(n)$ ，即为扫描线需要使用的空间 。

参考:

1.https://leetcode.cn/problems/rectangle-area-ii/solution/by-capital-worker-7efv/

2.https://leetcode.cn/problems/rectangle-area-ii/solution/ju-xing-mian-ji-ii-by-leetcode-solution-ulqz/