splay学习笔记重制版

本文主要是介绍splay学习笔记重制版，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

以前写的学习笔记：传送门
但是之前写的比较杂乱，这里重制一下

问题背景

假设我们要维护一个数据结构，支持插入、删除、查询某个值的排名，查询第 $k$ 大的值等操作。
最直接的想法是用二叉搜索树，也就是左子树权值<根节点权值<右子树权值的数据结构。查询时，如果目标值小于根节点就往左走，否则往右走。
但是二叉搜索树的深度是没法保证的，树高可以达到 $O (n)$ 级别，这样我们的操作都是 $O (n)$ 的。
因此这里我们需要使用平衡树，通过一些操作来维持树的平衡，让单次操作变成 $O(\log n)$ 的复杂度。

旋转操作

我们看下面这棵二叉搜索树，它的权值满足：X<B<Y<A<C。
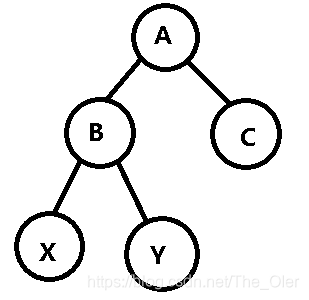
在这里插入图片描述
假设我们想要把B节点旋转到根节点，我们先把B往上提起来：

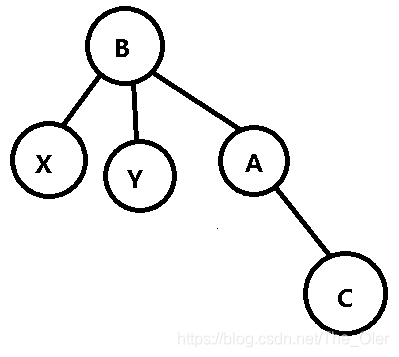
然后为了维持二叉搜索树的性质，根据X<B<Y<A<C的权值关系，我们把Y连到A上：

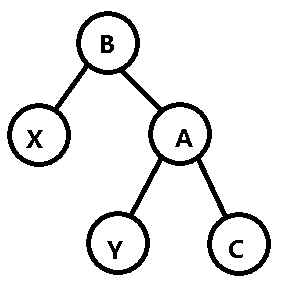
上面演示的是右旋（zig）操作，左旋（zag）类似，对A节点左旋就得到原来的树。
（具体实现的时候不用纠结是左旋还是右旋，可以通过同一个rotate函数旋转，见实现细节部分）
这样我们就把B节点往上旋转了一次，使它的深度减少了1。
我们不断旋转目标节点，直到旋转到根的这一过程，称为伸展（splay）。

双旋操作

在把一个节点一直转到根（即splay操作）的过程中，如果我们只是一直旋转同一个节点（即单旋），我们发现这样没法保证树高维持在平均 $O(\log n)$ 。
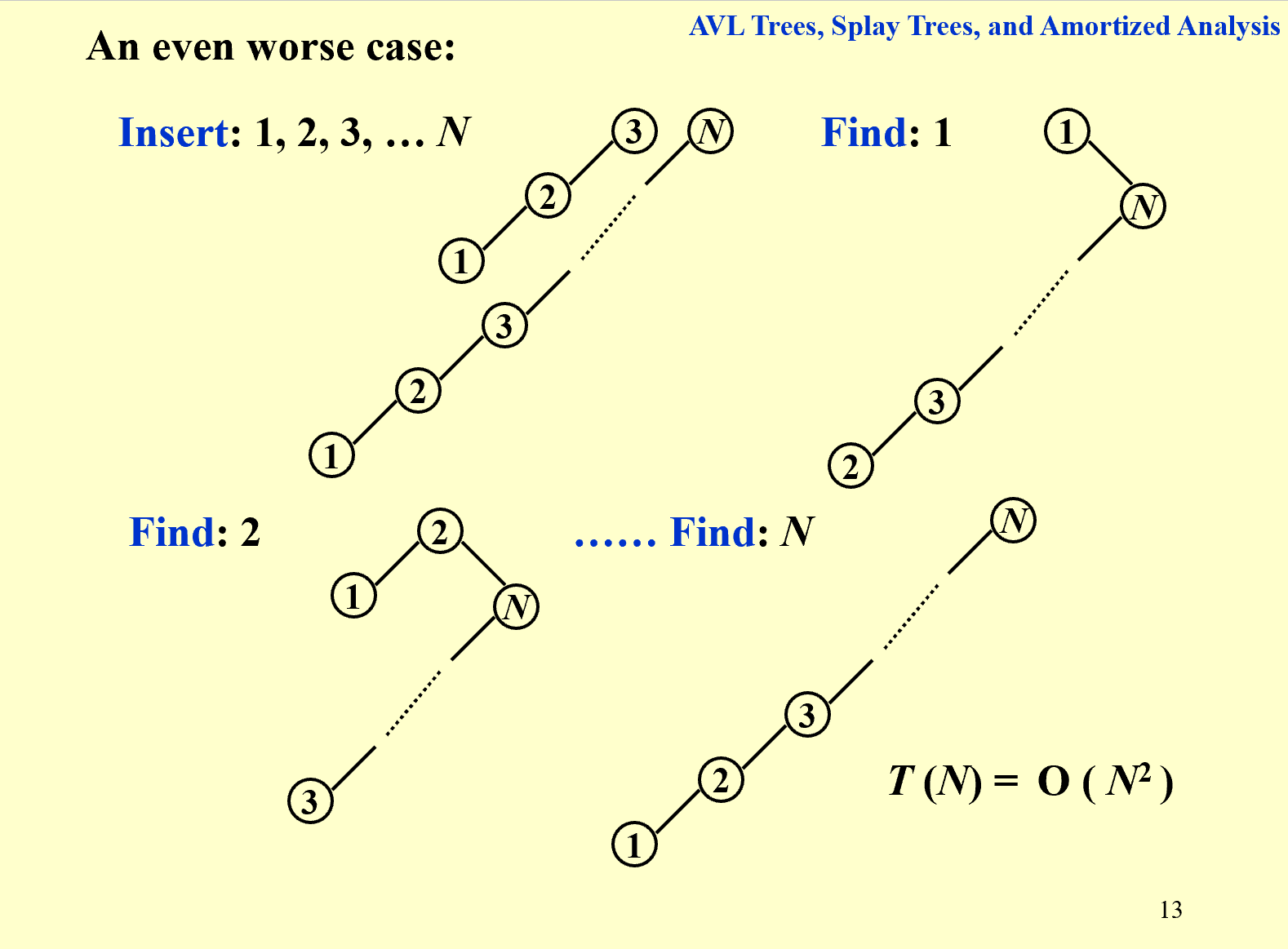
在这里插入图片描述
我们需要进行双旋操作。假设需要旋转的节点是X，X的父节点为P。假如P是根节点，那只需要旋转X就可以了，比较简单。主要讨论P不是根节点的两种情况：
1.X与P所在分支反向（即X和P一个是左孩子，一个是右孩子）
这种情况我们旋转X两次就可以了。由于X和P所在分支方向相反，所以这两次旋转一次是左旋，一次是右旋。

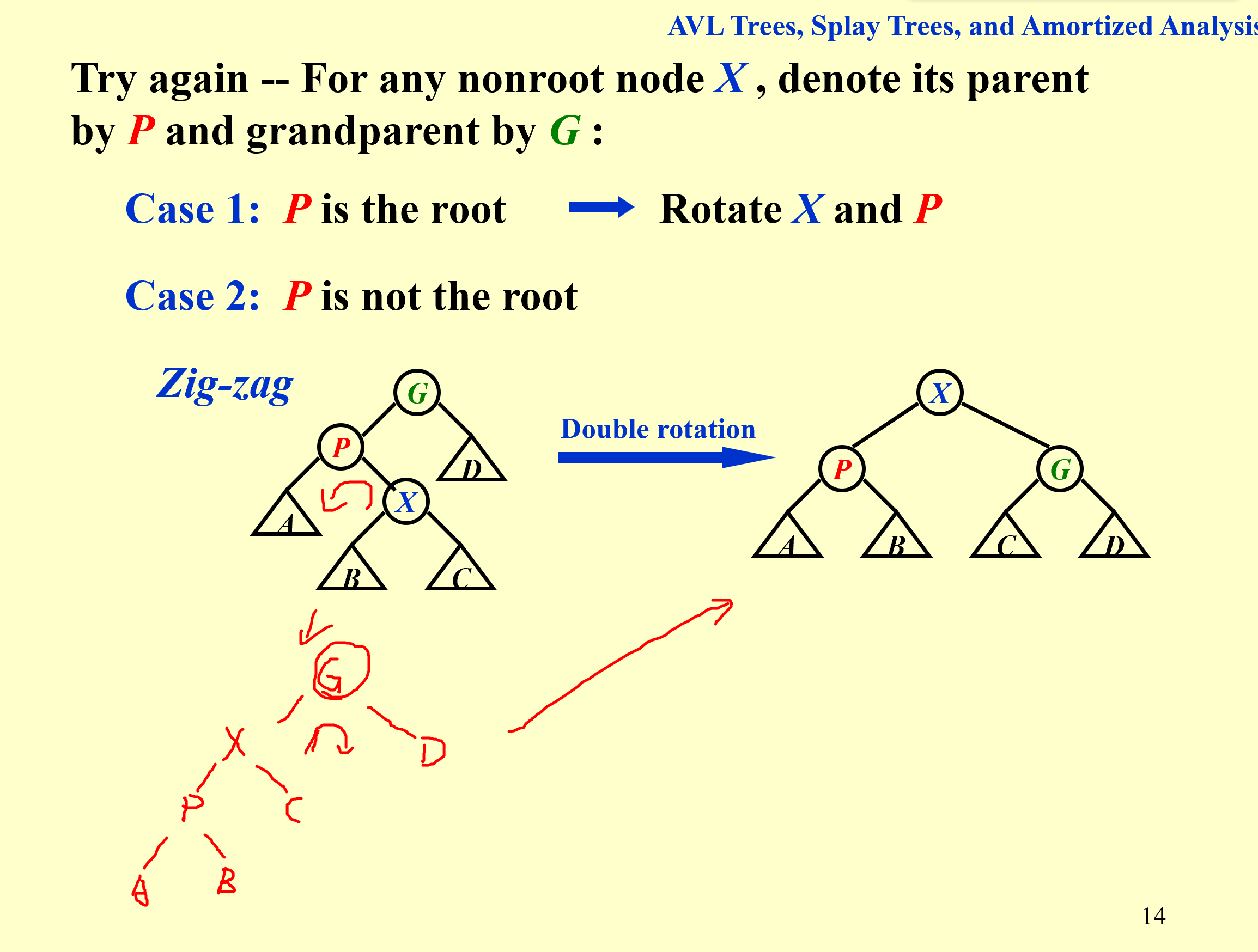
在这里插入图片描述
2.X与P所在分支同向（即X和P同为左孩子或右孩子）
如果这里还是旋转X两次，就会导致上面提到的问题，我们的树高没法控制。
所以这种情况我们要先旋转P，再旋转X。

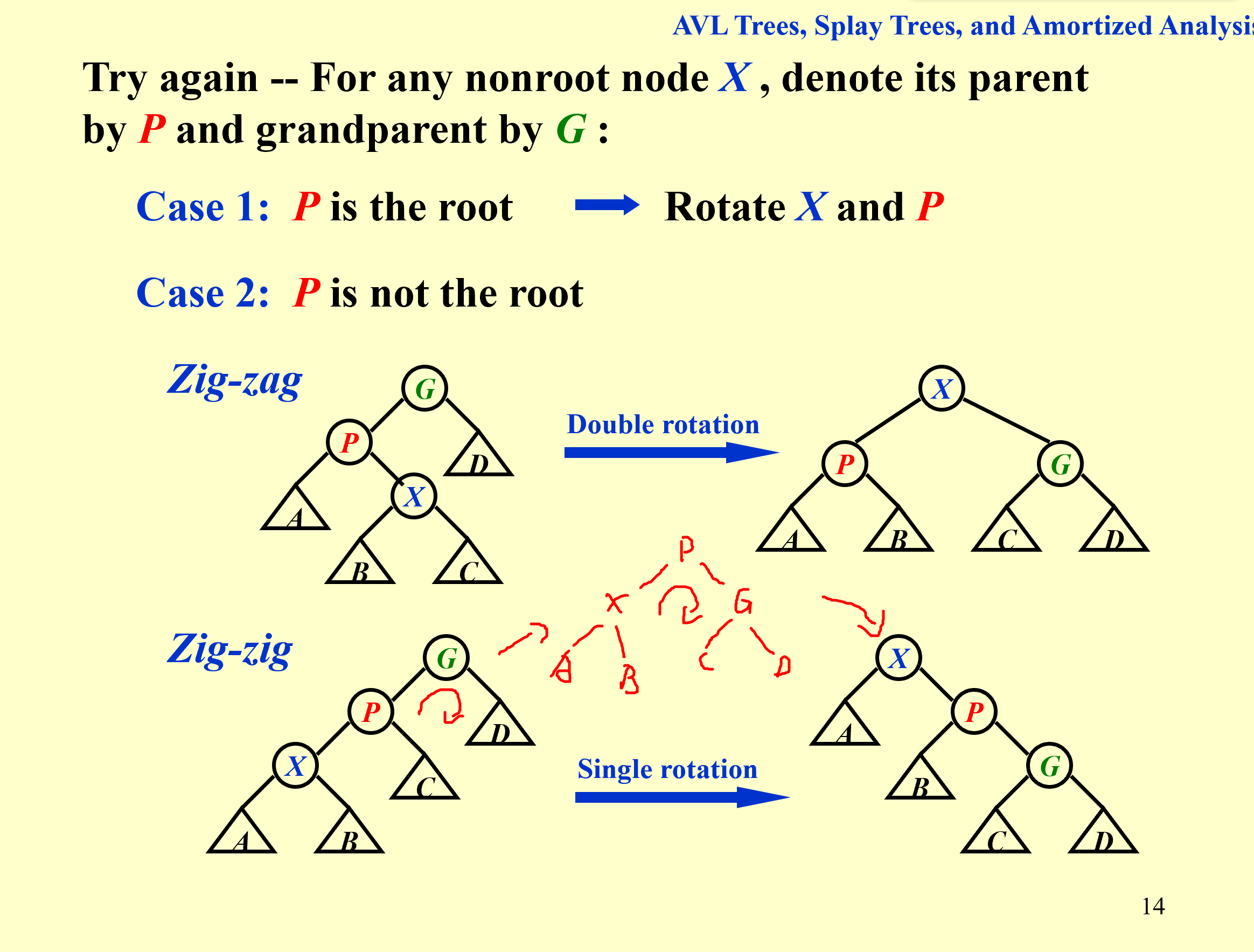
总结：同向先转父节点，反向转两次自己。

时间复杂度分析

这部分可以全部跳过，只需要知道均摊复杂度为 $O(\log n)$ 即可。

均摊时间复杂度介绍

均摊时间复杂度，其实就是每一次操作平均下来的复杂度。在多次操作中，一些操作用时比较长，另一些操作用时比较短，我们需要计算所有复杂度加起来除以操作数得到的结果。
在splay树中，我们把“将任意一个节点旋转到根节点”称为一次操作。
单次操作的复杂度最高为 $O (n)$ ，但是总的均摊复杂度为 $O(\log n)$ 。

均摊时间复杂度计算

这个在以前写的学习笔记的最后部分有介绍，但是写得很乱。我们这里介绍势能分析方法。
假设我们有 $m$ 个操作，开销分别为 $c_1,c_2,...,c_m$ 。那么这 $m$ 次操作的总复杂度为 $\sum\limits_{i=1}^{m}c_i$ ，单次操作的复杂度为 $\frac{\sum\limits_{i=1}^mc_i}{m}$ 。
通常 $\sum\limits_{i=1}^mc_i$ 是不太好算的，因此我们可以引入一个势能函数 $\Phi$ （这个势能函数是我们根据具体问题设计的，不是一个固定的函数）， $\Phi(D_i)$ 表示第 $i$ 次操作之后数据结构的“势能”。
定义 $t_i=c_i+\Phi(D_i)-\Phi(D_{i-1})$ ，表示一种操作的开销与引起的势能变化之和。
那么 $\sum\limits_{i=1}^mt_i=\sum\limits_{i=1}^m(c_i+\Phi(D_i)-\Phi(D_{i-1}))=\sum\limits_{i=1}^mc_i+\Phi(D_m)-\Phi(D_0)$ 。
只要我们合理地设计这个 $\Phi$ ，使得 $\sum\limits_{i=1}^mt_i$ 能算出来，而且 $\Phi(D_m)\ge\Phi(D_0)$ ，我们就可以得到 $\sum\limits_{i=1}^mc_i\le\sum\limits_{i=1}^mt_i$ ，并把 $\frac{\sum\limits_{i=1}^mt_i}{m}$ 当作实际上的单次时间复杂度（即均摊复杂度，amortized cost）。

splay均摊复杂度分析

下面分析过程中， $\log$ 的底数都为2（e.g. $\log 1024 = 10$ ）。
我们定义splay树中某个节点 $x$ 的子树大小为 $S (x)$ ，势能 $R(x)=\log S(x)$ 。（S代表size，R代表rank）
整棵树的势能 $\Phi(T)=\sum\limits_{i\in T}R(i)=\sum\limits_{i\in T}\log S(i)$ 。

在将某个节点X splay到根节点的过程中，总共有3种情况：（设X的父亲为P）
1.P为根节点，则旋转X。
2.X和P同向，先旋转P，再旋转X。
3.X和P反向，旋转两次X。
其中第一种情况最多发生一次，因为发生之后X就到根节点了。
设第 $i$ 次旋转的均摊复杂度为 $t_i$ ，则一次splay操作的复杂度为 $\sum t_i$ 。
我们希望证明后两种情况旋转一次的 $t_i\le3(R_2(X)-R_1(X))$ ，第一种 $t_i\le 3(R_2(X)-R_1(X))+1$ 。

第一种情况：P为根节点，旋转X。
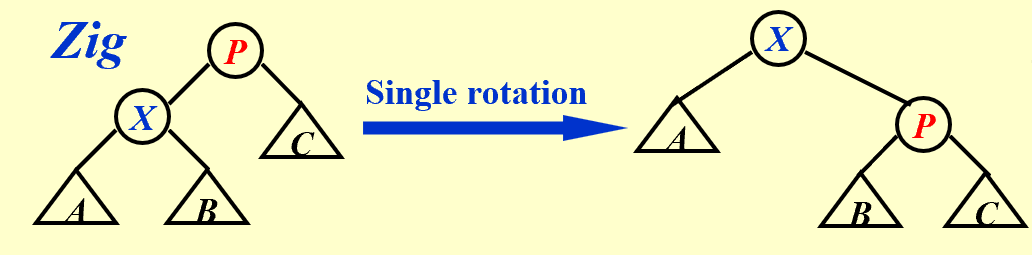
在这里插入图片描述
这种情况， $c_i=1$ ，只有X和P节点的势能发生了变化（其它节点的子树大小不变）
那么 $t_i=c_i+\Phi(T_2)-\Phi(T_1)=1+R_2(X)-R_1(X)+R_2(P)-R_1(P)$
由于 $R_2(P)<R_1(P)$ ，所以 $t_i<1+R_2(X)-R_1(X)\le 1+3(R_2(X)-R_1(X))$

第二种情况：X和P同向，先旋转P，再旋转X。
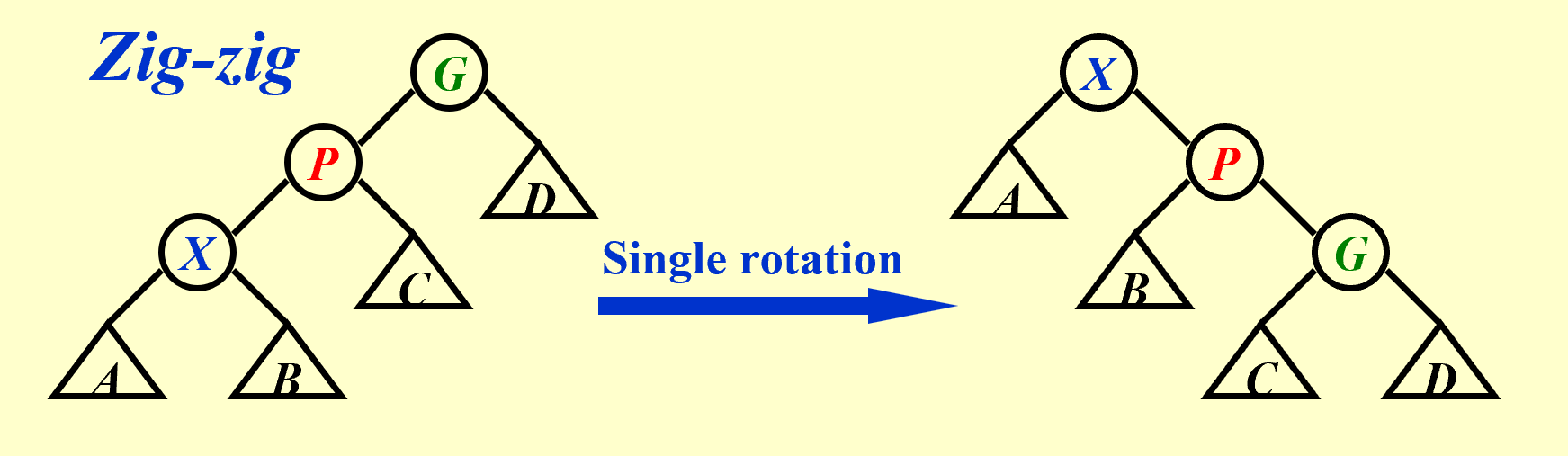
在这里插入图片描述
这里旋转了两次，所以 $c_i=2$ 。另外，X，P，G节点的势能发生了变化。
$t_i=2+\Phi(T_2)-\Phi(T_1)=2+R_2(X)-R_1(X)+R_2(P)-R_1(P)+R_2(G)-R_1(G)$
这里 $R_2(X)=R_1(G)$ ，所以 $t_i=2+R_2(P)+R_2(G)-R_1(X)-R_1(P)$ 。
注意到（注意不到怎么办？）：
$2R_2(X)-R_2(G)-R_1(X)=\log \frac{S_2(X)^2}{S_2(G)S_1(X)}=\log\frac{(S_2(G)+S_1(X)+1)^2}{S_2(G)S_1(X)}$ 。
令 $a=S_2(G),b=S_1(X)$ ，则 $2R_2(X)-R_2(G)-R_1(X)=\log\frac{(a+b+1)^2}{ab}\ge\log\frac{(a+b)^2}{ab}\ge\log 4=2$ 。
因此： $t_i\le (2R_2(X)-R_2(G)-R_1(X))+R_2(P)+R_2(G)-R_1(X)-R_1(P)$
$2R_2(X)-2R_1(X)+R_2(P)-R_1(P)$
又由于 $R_2(P)\le R_2(X),R_1(P)\ge R_1(X)$ ，
所以 $t_i\le 3(R_2(X)-R_1(X))$ 。

第三种情况：X和P反向，旋转两次X。
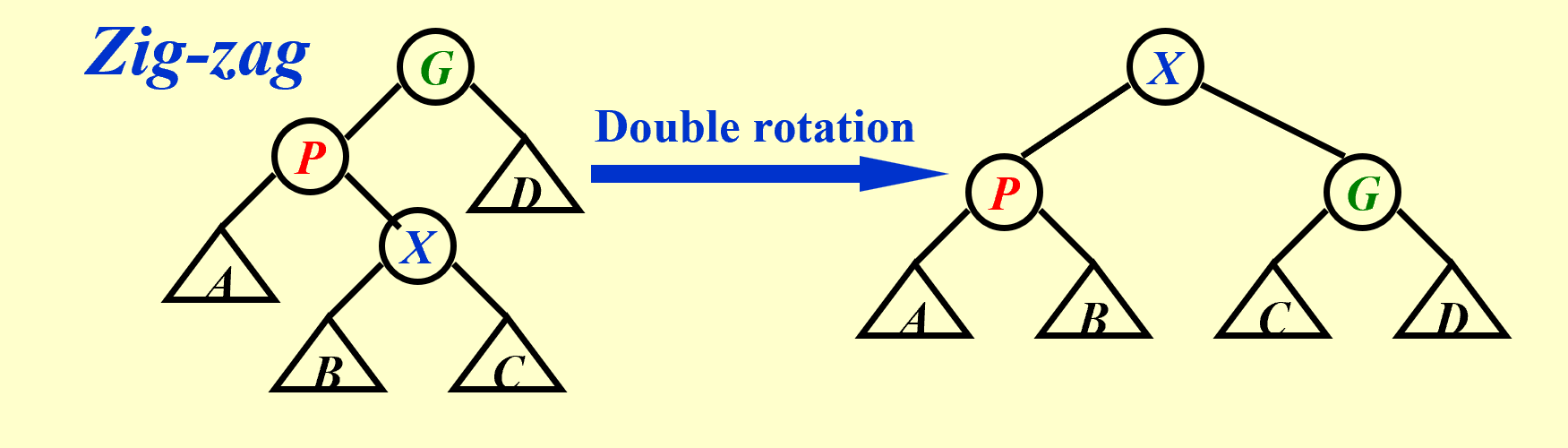
在这里插入图片描述
类似地，可以得到 $t_i\le 3(R_2(X)-R_1(X))$ 。

上面我们证明了后两种旋转的 $t_i\le3(R_2(X)-R_1(X))$ ，第一种 $t_i\le 3(R_2(X)-R_1(X))+1$ 。
由于第一种情况有且仅有一次，所以我们把所有旋转的 $t_i$ 加起来，消去中间项，得到 $\sum t_i=3(R(X')-R(X))+1$ 。
因为 $\sum t_i$ 就表示把一个节点splay到根的均摊复杂度，所以均摊复杂度即为 $O(\log n)$ 。
对于 $m$ 次splay操作，总复杂度为 $m*O(\log n)+\Phi(T_m)-\Phi(T_0)$ 。树在成为一条链时势能取到最大值 $n\log n$ ，所以 $m$ 次splay的总复杂度为 $O((m+n)\log n)$ 。其中 $n$ 为节点数。

splay树的操作

不管以什么顺序选节点，我们一个个把它们splay到根，最后每次的均摊复杂度为 $O(\log n)$ 。
因此，无论是插入、删除、查询还是其他操作，我们按二叉查找树的操作进行，然后把目标节点splay到根。
由于插入、删除、查询等操作和splay操作访问的都是一样的节点，所以它们的时间复杂度和splay操作是同一个级别的，都是 $O(\log n)$ 。

实现细节

//splay树定义
struct node {int father;int val;int ch[2];		//左右孩子
} w[Size];
int chk(int x) {		//chk(x)=0表示x为左孩子，=1表示x为右孩子return w[w[x].father].ch[1]==x;
}
void connect(int x,int fa,int k) {w[x].father=fa;w[fa].ch[k]=x;
}
void rotate(int x) {	//把x往上旋转一次int y=w[x].father;int z=w[y].father;int yson=chk(x),zson=chk(y);connect(w[x].ch[yson^1],y,yson);connect(y,x,yson^1);connect(x,z,zson);
}
void splay(int x,int goal) {	//把节点x旋转到goal的孩子的位置，goal=0表示旋转到根 int fa;while((fa=w[x].father)!=goal) {if(w[fa].father!=goal) {if(chk(x)==chk(fa)) {rotate(fa);} else {rotate(x);}}rotate(x);}if(!goal)	root=x;
}