本文主要是介绍使用Julia语言及R语言进行格拉布斯检验,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
在日常的计量检测工作中经常会处理各种数据,在处理数据之前会提前使用格拉布斯准则查看数据中是否存在异常值,如果存在异常值的话应该重新进行计量检测,没有异常值则对数据进行下一步操作。判断异常值常用的格拉布斯方法基于数据来自正态分布的假设,通过计算格拉布斯统计量(G值)并与临界值进行比较来判断数据点是否为离群值,分为双边检验和单侧检验,双边检验用于检测数据集中最大和最小值是否为异常值,而单侧检验则仅关注最大值或最小值。
计算过程及Markdown版本公式代码
先计算平均值和标准差


Markdown版本的公式代码:
**计算样本均值和标准差**:
计算给定数据集的样本均值(\(\overline{x}\))和样本标准差(\(s\)),其中样本标准差使用 \(n - 1\) 作为分母(\(n\) 为样本量)。
样品均值计算公式:
$$
\overline{x} = \frac{1}{n} \sum_{i=1}^{n} x_i
$$
其中: - $\overline{x}$ 表示样本均值
- $n$ 表示样本中的观测值数量
- $x_i$ 表示样本中的第 $i$ 个观测值
- $\sum_{i=1}^{n} x_i$ 表示从第1个观测值到第$n$个观测值的和 标准差计算公式:
$$
s = \sqrt{\frac{1}{n-1} \sum_{i=1}^{n} (x_i - \overline{x})^2}
$$
其中: - $s$ 表示样本标准差
- $n$ 表示样本中的观测值数量
- $x_i$ 表示样本中的第 $i$ 个观测值
- $\overline{x}$ 表示样本均值
- $\sum_{i=1}^{n} (x_i - \overline{x})^2$ 表示各观测值与均值之差的平方和随后计算格拉布斯统计量Gi并找出最大的格拉布斯统计量,通常取置信度95%,显著性水平a为0.05,根据样本量和显著性水平查找格拉布斯检验的临界值 G(a,n)


Markdown版本的公式代码:
**计算格拉布斯统计量**:
1.对于数据集中的每个数据点 \(x_i\),计算其格拉布斯统计量 \(G_i\),公式如下:\[ G_i = \frac{|x_i - \overline{x}|}{s} \]这里,\(|x_i - \overline{x}|\) 是数据点 \(x_i\) 与样本均值 \(\overline{x}\) 之差的绝对值。
2. **找出最大格拉布斯统计量**:从所有计算出的 \(G_i\) 值中找出最大值 \(G_{\text{max}}\)。
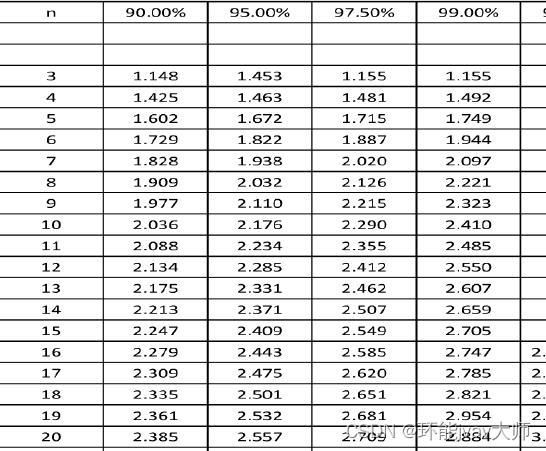
3. **确定显著性水平和临界值**:选择一个显著性水平 \(\alpha\)(如 0.05 或 0.01),并查找或计算对应样本量和显著性水平的格拉布斯临界值 \(G_{\text{critical}}\)。临界值通常通过查表或使用统计软件获得。
4. **比较最大格拉布斯统计量与临界值**:如果 \(G_{\text{max}} > G_{\text{critical}}\),则拒绝原假设,认为最大格拉布斯统计量对应的数据点是离群值。否则,接受原假设,认为数据集中没有离群值。5.格拉布斯检验法的公式:- 格拉布斯统计量:\(G_i = \frac{|x_i - \overline{x}|}{s}\)
- 最大格拉布斯统计量:\(G_{\text{max}} = \max_{1 \leq i \leq n} G_i\)我在平时简单应用的时候是计算器算一下然后查表
Julia语言实现
需要先下载 Statistics包
using Pkg
Pkg.add("Statistics")using Statistics function grubbs_test(data::Vector{Float64}, alpha::Float64) n = length(data) if n < 3 error("Sample size must be at least 3 for Grubbs' test") end g_critical = 1.933 mean_val = mean(data) std_dev = std(data, corrected=true) # 使用n-1计算样本标准差 # 计算每个点与均值的绝对差值,并除以标准差,然后找出最大的g值 g_values = abs.(data .- mean_val) ./ std_dev g_max = maximum(g_values) # 判断是否存在离群值 if g_max > g_critical return (true, g_max) else return (false, g_max) end
end data = [0.55, 0.51, 0.56, 0.49, 0.52, 0.12]
alpha = 0.05 # 显著性水平
has_outlier, g_max = grubbs_test(data, alpha)
println("Has outlier: $has_outlier")
println("G max: $g_max")运行结果:存在异常值,最大G值为2.017,目前只是判断了这组样本数据中有没有存在异常值,但还未揪出异常值,效果并不太好。此时,一刻也没有为Julia加速,立刻赶到战场的是R语言。

R语言实现
先下载R包 outliers 然后:
library(outliers)data <- c(0.55, 0.51, 0.56, 0.49, 0.52, 0.12)
# 执行格拉布斯检验
result <- grubbs.test(data)
print(result)运行结果 ,四行代码快速解决战斗,坑爹异常值是0.12。

这篇关于使用Julia语言及R语言进行格拉布斯检验的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




