本文主要是介绍前缀和/前缀和+后缀和?!!:瞬秒Leetcode 742.寻找数组的中心下标,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
题目
给你一个整数数组 nums ,请计算数组的 中心下标 。
数组 中心下标 是数组的一个下标,其左侧所有元素相加的和等于右侧所有元素相加的和。
如果中心下标位于数组最左端,那么左侧数之和视为 0 ,因为在下标的左侧不存在元素。这一点对于中心下标位于数组最右端同样适用。
如果数组有多个中心下标,应该返回 最靠近左边 的那一个。如果数组不存在中心下标,返回 -1 。
示例 1:
输入:nums = [1,7,3,6,5,6] 输出:3 解释: 中心下标是 3 。 左侧数之和 sum = nums[0] + nums[1] + nums[2] = 1 + 7 + 3 = 11 , 右侧数之和 sum = nums[4] + nums[5] = 5 + 6 = 11 ,二者相等。
示例 2:
输入:nums = [1, 2, 3] 输出:-1 解释: 数组中不存在满足此条件的中心下标。
示例 3:
输入:nums = [2, 1, -1] 输出:0 解释: 中心下标是 0 。 左侧数之和 sum = 0 ,(下标 0 左侧不存在元素), 右侧数之和 sum = nums[1] + nums[2] = 1 + -1 = 0 。

阅读题目求一个下标左右两边和是否相等,一眼顶真前缀和没跑,接下来分为两个思路来解决此问题:解法一中规中矩使用完全的前缀和来解决,解法二使用前缀和加后缀和更加需要对前缀和思想有深刻的理解。
前缀和思路
前缀和是什么:前缀和一镜到底:秒懂一、二维前缀和的逻辑与实现方式
首先可以构建名为dp的前缀和数组,这样比起每次都去暴力的遍历判断节省不少的时间,因为此时原生数组的下标是从0开始的,所以不能直接套用一维前缀和模板,而是先要对其进行处理,得出符合此题的动态转移方程,dp[1]所对应的是nums[0],所以dp[i]=dp[i-1]+nums[i-1]。
题目要求求判断i之前和之后是否相等,而求i之前的和只需要直接查找dp[i-1]就可以得到,查找i之后的只需要拿dp[n]-dp[i]就可以得到。
所以此题的使用公式为:dp[i-1]==dp[n]-dp[i];
代码实现
class Solution {
public:int pivotIndex(vector<int>& nums) {vector<int> dp(nums.size()+1);int ret=0,n=nums.size();//构建前缀和数组for(int i=1;i<=nums.size();i++){dp[i]=dp[i-1]+nums[i-1];}//使用前缀和数组for(int i=1;i<=nums.size();i++){if(dp[i-1]==dp[n]-dp[i]) return i-1;}return -1;}
};前缀和+后缀和思路
除了直接通过前缀和数组进行减法操作后得出i之前和之后的数来判断是否相等以外,还可以在构建前缀和数组时就直接构建出俩个数组,一个记录每个节点左边的所有元素之和就是前缀和,一个记录每个节点右边的所有元素的和,构建好后只需要一次遍历从左往右遍历时比较两棵树对应的值就能找到最左符合要求的节点。
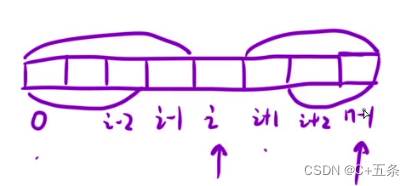
注意这里的每个节点存的时它之前的数的和,所以当前节点存的数是不包含nums数组中相对应的该位置的数的,而且此时所构建的前后缀和数组下标是直接从0开始的而题目说最靠左或右的左或右的和都为零,所以此时需要处理一下边界,所以前缀和数组0的位置赋值为0,后缀和n-1的位置赋值为0。然后构造数组时直接从第二个元素开始构造。从而得出前缀和的公式:
dpf[i]=dp[i-1]+nums[i-1];
后缀和公式:
dpe[i]=dpe[i+1]+dpe[i+1];
然后直接遍历进行比较就可以。
代码实现
class Solution {
public:int pivotIndex(vector<int>& nums) {vector<int> dpf(nums.size()),dpe(nums.size());dpf[0]=0;dpe[nums.size()-1]=0;for(int i=1;i<nums.size();i++)//构造前缀和数组{dpf[i]=dpf[i-1]+nums[i-1];}for(int i=nums.size()-2;i>=0;i--)//构造后缀和数组{dpe[i]=dpe[i+1]+nums[i+1];}for(int i=0;i<nums.size();i++){if(dpf[i]==dpe[i]) return i;}return -1;}
};这篇关于前缀和/前缀和+后缀和?!!:瞬秒Leetcode 742.寻找数组的中心下标的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




