漫漫数学之旅035

本文主要是介绍漫漫数学之旅035，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

经典格言

完美的数和完美的人是同样罕见的。——黎勒•笛卡尔（René Descrates）

完美的数和完美的人都是极为罕见的。这句话表达了一个哲学观点，即无论是在数学领域还是人类自身，完美都是不容易达到的高标准。

完美的数，又称为完全数，是一种自然数，它恰好等于其所有真因子（除自身以外的约数）之和。例如，6是一个完美数，因为1、2、3（即6的所有真因子）相加正好等于6。这种数在数学中不仅因其独特性而备受瞩目，还因其稀有性和某种数学美的体现而被赋予特殊意义。截至目前为止，只发现了47个完美数，而且它们全都是偶数。是否存在奇数的完美数，至今没有定论，这使得完美数的研究成为数学中的一个难题和挑战。

而完美的人的概念则更为复杂。在人类的道德、行为、性格等各方面要达到“完美”的标准是极其困难的。每个人都会有优点和缺点，都有成长和改进的空间。因此，当我们说完美的人时，我们可能指的是那些在某一时刻，某一方面表现出色的人，但很难找到一个在所有方面都无可挑剔的人。

笛卡尔的这句话提醒我们，无论是在追求数学上的完美解还是生活中的完美境界，我们都应当认识到完美是一个值得追求但难以实现的理想状态。这种认识可以帮助我们保持谦逊，同时激励我们不断前进，向着更高的标准努力。

数学习题

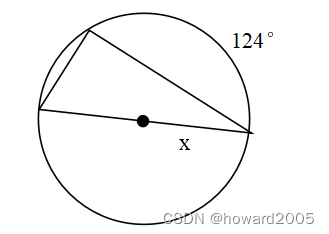
古今评注

一码就是一码，这话听起来似乎毋庸置疑，就像我们常说的“一加一等于二”一样自然。但如果我们追溯到古代，在没有现代精密测量工具的年代，"一码"的长度其实是相当随意和相对的，甚至可能随着国王的心情或体型变化而变化。

想象一下，英王亨利一世某天醒来，心情大好，他决定把自己的指尖到鼻子的距离定义为一码。于是，随从们赶紧找来布尺，小心翼翼地量了起来。这可真是个艰巨的任务，毕竟国王的鼻子不是每天都能轻易量到的。最终，他们宣布一码就是这么多英寸，然后刻在了一块石板上，供后人参考。

再说查理曼大帝，这位身材魁梧的君主，他的步长显然要比普通士兵来得霸气许多。于是，人们便以查理曼的步伐来定义英尺，仿佛是在说：“看，这就是伟大皇帝的风范！”不过，如果查理曼那天刚好腿脚不便，或许我们今天使用的英尺会短得多。

这些古代的定义方式，虽然有趣，却也暴露出了一个问题：标准是会变的，而且是随着某个人的特定情况而变的。这就导致了历史上的混乱，不同地区的“码”和“英尺”长度千差万别，直到现代精确的度量衡系统确立，才结束了这种混乱局面。

所以，尽管我们现在有了严格的国际单位制，但在古代，一码确实不总是一码，它可能随着国王的鼻子长短、步子大小而有所不同。这样的历史趣闻，不仅让我们对古人的创造力和适应性感到敬佩，也让我们庆幸，至少现在我们不用担心因为国王的鼻子变长而需要重新学习尺寸单位了。

名人小传 - 黎勒•笛卡尔

勒内·笛卡尔（René Descartes），一个响当当的名字，既是哲学圈的大腕儿，又是数学界的巨星，1596年3月31日在法国图赖讷拉海呱呱坠地，这个地方后来为了纪念他的伟大成就，改名为笛卡尔市。

笛卡尔小时候体弱多病，8岁就被送进了皇家大亨利学院学习，校方特批他可以在床上读书，不用早晨赶着去上课。这种特殊的待遇让他养成了爱思考的习惯，尤其是对数学和物理情有独钟。

长大后的笛卡尔，不仅在哲学上提出了“我思故我在”这样的金句，还在数学上发明了解析几何，把代数和几何结合在了一起，让几何图形也能用方程来表示，这可是数学史上的一大步。

他的怀疑论思想，就是不停地质疑一切，直到找到不容置疑的真理。这种方法被他用来证明上帝的存在，从而确立了心物二元论的基础。

笛卡尔的一生可谓是充满智慧和成就，他的思想至今仍然影响着我们的世界。他的名言“我思故我在”不仅是哲学课堂上的常客，也是很多人自我反思的出发点。而他在数学上的贡献，更是让几何学进入了一个全新的时代。

这篇关于漫漫数学之旅035的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---