本文主要是介绍C++第13周(春)项目3 - 与圆心相连的直线,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
课程首页在:http://blog.csdn.net/sxhelijian/article/details/11890759,内有完整教学方案及资源链接
【项目3 - 与圆心相连的直线】
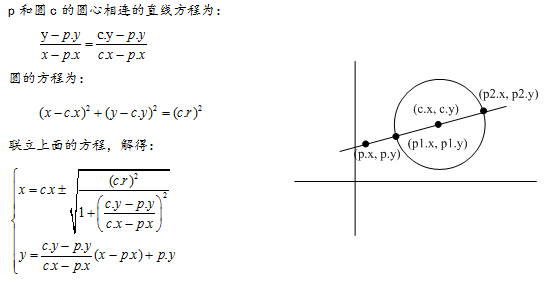
在项目1中定义的Point(点)类和Circle(圆)类基础上,设计一种方案,输出给定一点p与圆心相连成的直线与圆的两个交点。
提示:
方案1:用引用类型参数获得结果
#include <iostream>
#include<Cmath>
using namespace std;
class Circle; //由于在Point中声明友元函数crossover_point中参数中用了Circle,需要提前声明
class Point
{
public:Point(double a=0,double b=0):x(a),y(b) {} //构造函数friend ostream & operator<<(ostream &,const Point &);//重载运算符“<<”friend void crossover_point(Point &p,Circle &c, Point &p1,Point &p2 ) ; //求交点的友元函数
protected: //受保护成员double x,y;
};
ostream & operator<<(ostream &output,const Point &p)
{output<<"["<<p.x<<","<<p.y<<"]";return output;
}class Circle:public Point //circle是Point类的公用派生类
{
public:Circle(double a=0,double b=0,double r=0):Point(a,b),radius(r) { } //构造函数friend ostream &operator<<(ostream &,const Circle &);//重载运算符“<<”friend void crossover_point(Point &p,Circle &c, Point &p1,Point &p2 ) ; //求交点的友元函数
protected:double radius;
};//重载运算符“<<”,使之按规定的形式输出圆的信息
ostream &operator<<(ostream &output,const Circle &c)
{output<<"Center=["<<c.x<<", "<<c.y<<"], r="<<c.radius;return output;
}//给定一点p,求出该点与圆c的圆心相连成的直线与圆的两个交点p1和p2
//关键问题是求得的交点如何返回
//方案1:利用引用类型的形式参数,注意,下面的p1和p2将“带回”求得的结果
//crossover_point函数已经声明为Point和Circle类的友元函数,类中私有成员可以直接访问
void crossover_point(Point &p, Circle &c, Point &p1,Point &p2 )
{p1.x = (c.x + sqrt(c.radius*c.radius/(1+((c.y-p.y)/(c.x-p.x))*((c.y-p.y)/(c.x-p.x)))));p2.x = (c.x - sqrt(c.radius*c.radius/(1+((c.y-p.y)/(c.x-p.x))*((c.y-p.y)/(c.x-p.x)))));p1.y = (p.y + (p1.x -p.x)*(c.y-p.y)/(c.x-p.x));p2.y = (p.y + (p2.x -p.x)*(c.y-p.y)/(c.x-p.x));
}int main( )
{Circle c1(3,2,4);Point p1(1,1),p2,p3;crossover_point(p1,c1, p2, p3);cout<<"点p1: "<<p1<<endl;cout<<"与圆c1: "<<c1<<endl;cout<<"的圆心相连,与圆交于两点,分别是:"<<endl;cout<<"交点1: "<<p2<<endl;cout<<"交点2: "<<p3<<endl;return 0;
}方案2:定义一个包含两个点的结构体,专门用于返回值(定义成类进行封装可能更好)
#include <iostream>
#include<Cmath>
using namespace std;
class Circle; //由于在Point中声明友元函数crossover_point中参数中用了Circle,需要提前声明
struct DoublePoint; //也先声明,Point中声明友元函数crossover_point中要用到
class Point
{
public:Point(double a=0,double b=0):x(a),y(b) {} //构造函数friend ostream & operator<<(ostream &,const Point &);//重载运算符“<<”friend DoublePoint crossover_point(Point &p,Circle &c) ; //求交点的友元函数
protected: //受保护成员double x,y;
};
ostream & operator<<(ostream &output,const Point &p)
{output<<"["<<p.x<<","<<p.y<<"]";return output;
}class Circle:public Point //circle是Point类的公用派生类
{
public:Circle(double a=0,double b=0,double r=0):Point(a,b),radius(r) { } //构造函数friend ostream &operator<<(ostream &,const Circle &);//重载运算符“<<”friend DoublePoint crossover_point(Point &p,Circle &c) ; //求交点的友元函数
protected:double radius;
};//重载运算符“<<”,使之按规定的形式输出圆的信息
ostream &operator<<(ostream &output,const Circle &c)
{output<<"Center=["<<c.x<<", "<<c.y<<"], r="<<c.radius;return output;
}struct DoublePoint //专门用于返回值的结构体类型
{Point p1;Point p2;
};//给定一点p,求出该点与圆c的圆心相连成的直线与圆的两个交点
//方案2:结果返回到DoublePoint类型的结构体中
//crossover_point函数已经声明为Point和Circle类的友元函数,类中私有成员可以直接访问
DoublePoint crossover_point(Point &p, Circle &c)
{DoublePoint pp;pp.p1.x = (c.x + sqrt(c.radius*c.radius/(1+((c.y-p.y)/(c.x-p.x))*((c.y-p.y)/(c.x-p.x)))));pp.p2.x = (c.x - sqrt(c.radius*c.radius/(1+((c.y-p.y)/(c.x-p.x))*((c.y-p.y)/(c.x-p.x)))));pp.p1.y = (p.y + (pp.p1.x -p.x)*(c.y-p.y)/(c.x-p.x));pp.p2.y = (p.y + (pp.p2.x -p.x)*(c.y-p.y)/(c.x-p.x));return pp;
}int main( )
{Circle c1(3,2,4);Point p1(1,1);DoublePoint pp;pp = crossover_point(p1,c1);cout<<"点p1: "<<p1<<endl;cout<<"与圆c1: "<<c1<<endl;cout<<"的圆心相连,与圆交于两点,分别是:"<<endl;cout<<"交点1: "<<pp.p1<<endl;cout<<"交点2: "<<pp.p2<<endl;return 0;
}=================== 迂者 贺利坚 CSDN博客专栏================= |== IT学子成长指导专栏 专栏文章的分类目录(不定期更新) ==| |== C++ 课堂在线专栏 贺利坚课程教学链接(分课程年级) ==| |== 我写的书——《逆袭大学——传给IT学子的正能量》 ==| ===== 为IT菜鸟起飞铺跑道,和学生一起享受快乐和激情的大学 ===== |
这篇关于C++第13周(春)项目3 - 与圆心相连的直线的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!