gym102443 D.Guess the Path

本文主要是介绍gym102443 D.Guess the Path，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

题目标题已经描述的很清楚了，明显是一道交互题，让你去向系统询问你猜的对不对，然后系统会给你反馈你那些点是取对了，然后你接着问，最多问10次。

当然这个10次包含明显的暗示，n,m都是1000，那么2^10刚好1024，暗示你用二分的操作来搞，你怎么样取构造这条路径才能达到一个最优，但是即使是想到了怎么去走但是如何去code还是很复杂。

队友盲猜了一个走的方式

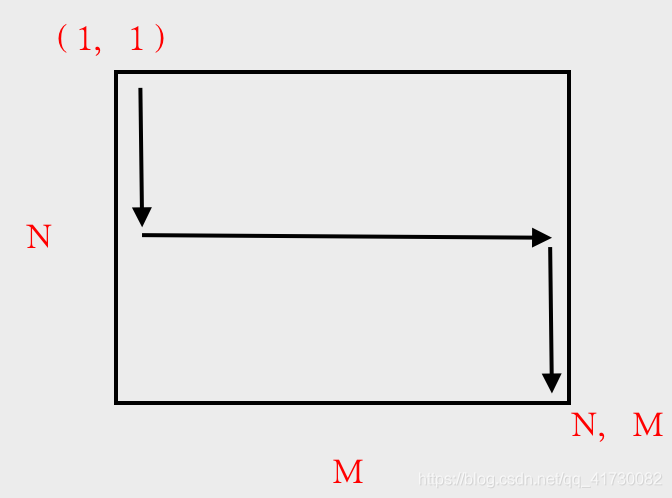
对于每一个左上点到右下点我们都选择这样得走的方式，记录每一个点的后趋与前驱。（对应代码solve函数）

如这第一次走得，至少也得经过三个点（自己理解），系统会返回你走过的点

我们分别记录我们走得每一个点装到一个vector里边去

然后开始遍历vector里的相邻的两个点，如果两个点位置相邻（就是两个点挨着）就直接走

如果两个点不相邻

那么第一个点的后驱如果在第一个点的下边，我们就选择走右边，设右边这个点的位置为pos1，反之亦然

如果第二个点的前驱在第二个点的左边，我们就选择他上边那个点，设上边那个点的位置为pos2,反之亦然

对pos1，pos2进行solve

类似就变成了二分的过程

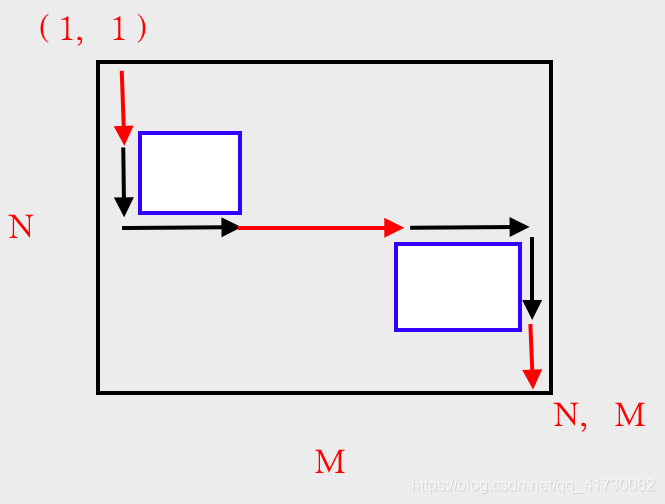
然后基本流程就就是这样，将确定的点丢到set里边，如果set里边的点==n+m-2的时候输出答案。

#include <bits/stdc++.h>
using namespace std;
#define pii(x,y) make_pair(x,y)
#define pr pair<int,int>
const int maxn=1e3+5;
int a[maxn][maxn];
map<pr,pr> pre,nex;
int n,m;
set<pr>ans;
vector<pr> v;
void solve(int sx,int sy,int ex,int ey)
{if(sx==ex&&sy==ey) return;pr pos=pii(sx,sy);int mid=(sx+ex+1)/2;while(pos.first<mid){cout<<"D";pre[pii(pos.first+1,pos.second)]=pii(pos.first,pos.second);nex[pii(pos.first,pos.second)]=pii(pos.first+1,pos.second);pos.first++;}while(pos.second<ey){cout<<"R";pre[pii(pos.first,pos.second+1)]=pii(pos.first,pos.second);nex[pii(pos.first,pos.second)]=pii(pos.first,pos.second+1);pos.second++;}while(pos.first<ex){cout<<"D";pre[pii(pos.first+1,pos.second)]=pii(pos.first,pos.second);nex[pii(pos.first,pos.second)]=pii(pos.first+1,pos.second);pos.first++;}
}
int main()
{cin>>n>>m;cout<<"? ";solve(1,1,n,m);cout<<endl;int c;cin>>c;int x,y;for(int i=1;i<=c;i++){cin>>x>>y;a[x][y]=1;ans.insert(pii(x,y));v.push_back(pii(x,y));}if(ans.size()==n+m-1){printf("! ");for(int i=1;i<v.size();i++){pr now=v[i],t=v[i-1];if(now.first==t.first+1) cout<<"D";else cout<<"R";}cout<<endl;return 0;}int tim=9;while(tim--){cout<<"? ";int cc=0;pr noww;noww.first=1,noww.second=1;cc++;while(1){if(a[noww.first+1][noww.second]) noww.first++,cc++,cout<<"D";else if(a[noww.first][noww.second+1]) noww.second++,cc++,cout<<"R";else{pr c=nex[noww];if(c.first==noww.first+1){cout<<"R";ans.insert(pii(noww.first,noww.second+1));pr d=v[cc];pr e=pre[d];if(e.first+1==d.first){ans.insert(pii(d.first,d.second-1));solve(noww.first,noww.second+1,d.first,d.second-1);cout<<"R";}else{ans.insert(pii(d.first-1,d.second));solve(noww.first,noww.second+1,d.first-1,d.second);cout<<"D";}noww=v[cc];cc++;}else{cout<<"D";ans.insert(pii(noww.first+1,noww.second));pr d=v[cc];pr e=pre[d];if(e.first+1==d.first){ans.insert(pii(d.first,d.second-1));solve(noww.first+1,noww.second,d.first,d.second-1);cout<<"R";}else{ans.insert(pii(d.first-1,d.second));solve(noww.first+1,noww.second,d.first-1,d.second);cout<<"D";}noww=v[cc];cc++;}}if(noww.first==n&&noww.second==m){cout<<endl;break;}}v.clear();cin>>c;int x,y;for(int i=1;i<=c;i++){cin>>x>>y;a[x][y]=1;ans.insert(pii(x,y));v.push_back(pii(x,y));}if(ans.size()==n+m-1){printf("! ");for(int i=1;i<v.size();i++){pr noww=v[i],pre=v[i-1];if(noww.first==pre.first+1) cout<<"D";else cout<<"R";}cout<<endl;return 0;}}
}/*
6 73
1 1
3 4
6 710
1 1
1 2
2 2
2 3
2 4
3 4
4 4
5 5
6 6
6 712
1 1
1 2
2 2
2 3
2 4
3 4
4 4
4 5
5 5
6 5
6 6
6 7*/

 

这篇关于gym102443 D.Guess the Path的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---