JZOJ 1495. 宝石（附加扫描线讲解）

JZOJ 1495. 宝石

题目大意：给你N个$(K+1)\times (K+1)$的正方形以及他们左上角的那个顶点的坐标和它的权值，求最大的覆盖的权值。
这一题可以用二维前缀和做，但是无法拿到满分。

满分做法：扫描线。

假如现在有这么两个长方形，权值都为1（不要问为什么是长方形，这里只是为了方便讲解而已），它们摆放如图：

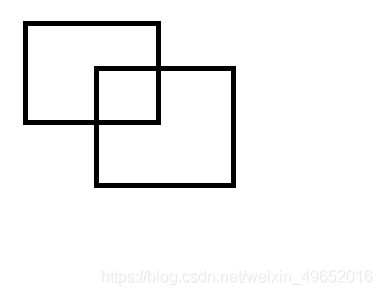
首先，我们把所有竖着的线给找出来。

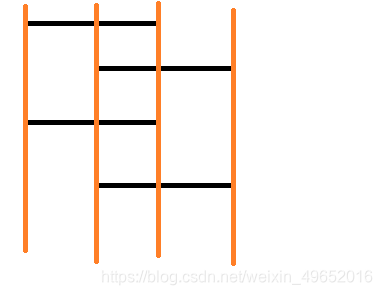
然后，我们就可以分别算出下面三个区域的最大覆盖权值了。

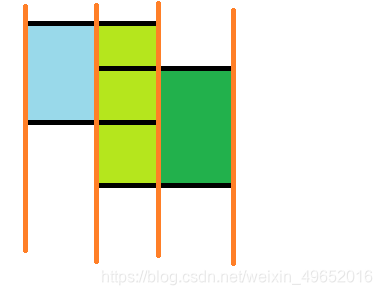
我们可以把所有的线按横坐标小到大排序，将这个几何图形分成了许多块，对于这一道题，我们可以这样计算：

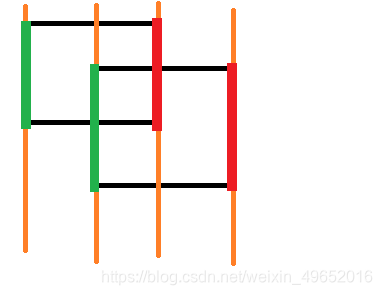
绿色边表示在这段区间内加上该矩形的权值，红色边表示减去该矩形的权值。
按照横坐标先排序，然后依次进行这些操作。
我们可以用线段树来实现区间加法。
大家可以结合伪代码理解一下：

struct line{int x,l,r,k;
}l[N*2];
bool cmp(line a,line b)
{if(a.x==b.x) return a.k<b.k;else return a.x<b.x;
}
...
scanf("%d%d%d",&m,&n,&k);
for(int i=1;i<=n;i++)
{scanf("%d%d%d",&x,&y,&z);l[i*2-1]=(line){x,y,y+k,z};l[i*2]=(line){x+k+1,y,y+k,-z};
}
sort(l+1,l+2*n+1,cmp);

注意有n+n条线。
这里解释一下排序每一条线的时候为什么横坐标相等小的要在上面，因为这里需要减掉一些正方形的贡献，再加上一些正方形的贡献，如果先加上再减去的话会重复计算。
为了使代码更简洁，建议减去的时候改为加上该数的相反数。
然后每一次线段树做完区间修改的时候再查询一下整颗线段树内的最大值就可以啦。
操作&查询部分的代码

for(int i=1;i<=n+n;i++)
{sgt.change(1,m,1,l[i].l,l[i].r,l[i].k);if(sgt.tr[1]+sgt.lz[1]>ans) ans=sgt.tr[1]+sgt.lz[1];
}

其实就是整个的核心了。
每一次在这一条线所覆盖的区间内加上这一条线的权值。
然后这一题就可以AC了。
相信线段树实现区间加减和区间求最值大家都会。
然后给出完整的代码：

#include<cstdio>
#include<algorithm>
#define ls (now<<1)
#define rs (now<<1|1)
#define mid ((l+r)>>1)
#define N 50010
using namespace std;
struct line{int x,l,r,k;
}l[N*2];
struct segment_tree{long long tr[N*4],lz[N*4];void change(int l,int r,int now,int L,int R,int a){if(R<l||r<L) return;if(L<=l&&r<=R){lz[now]+=a;return;}change(l,mid,ls,L,R,a);change(mid+1,r,rs,L,R,a);tr[now]=max(tr[ls]+lz[ls],tr[rs]+lz[rs]);}
}sgt;
bool cmp(line a,line b)
{if(a.x==b.x) return a.k<b.k;else return a.x<b.x;
}
int n,m,k,x,y,z;
long long ans;
int main()
{scanf("%d%d%d",&m,&n,&k);for(int i=1;i<=n;i++){scanf("%d%d%d",&x,&y,&z);l[i*2-1]=(line){x,y,y+k,z};l[i*2]=(line){x+k+1,y,y+k,-z};}sort(l+1,l+2*n+1,cmp);for(int i=1;i<=n+n;i++){sgt.change(1,m,1,l[i].l,l[i].r,l[i].k);if(sgt.tr[1]+sgt.lz[1]>ans) ans=sgt.tr[1]+sgt.lz[1];}printf("%lld",ans);return 0;
}