本文主要是介绍关系模式判断候候选关键字 与 函数依赖无损连接,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
关系模式判断候候选关键字 与 函数依赖无损连接
例题:设关系模式R(U, F),其中R上的属性集U={A, B, C, D, E},R上的函数依赖集F={A→B,DE→B,CB→E,E→A,B→D}。( )为关系R的候选关键字。分解( )是无损连接,并保持函数依赖的。
问题一:
A: AB B:DE C:CE D:DB
问题二:
A.p={R1(AC),R2(ED),R3(B)}
B.p={R1(AC),R2(E),R3(DB)}
C.p={R1(AC),R2(ED),R3(AB)}
D.p={R1(ABC),R2(ED),R3(ACE)}
解:
问题一:
依据每个选项以及函数依赖集F判断是否能够遍历全图;

嗯...图太丑,见谅! 答案:CE;
问题二: 答案:D

原则:关系模式包含此列头,那么记为a,下标为列号(1开始);如果不包含此列头,那么记为b,下标为坐标.
依据函数依赖集,反复计算,直到无法计算为止.
计算方法:例: DE->B 找到,DE 2列相同值的行,目标列B中如果有a,则记为a;没有a,记为此列最小b;
反复计算后可得出:
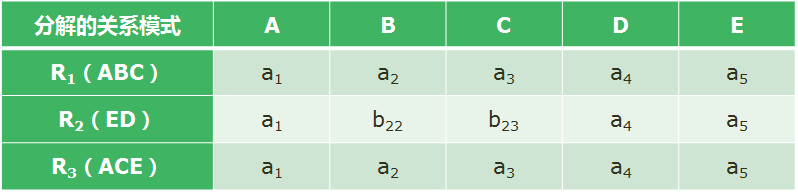
行一全部为a,则无损分解.(某一行全部为a即可)
这篇关于关系模式判断候候选关键字 与 函数依赖无损连接的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





