本文主要是介绍数电学习笔记——逻辑函数及其描述方法,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
一、逻辑函数
二、逻辑函数的描述方法
1、逻辑真值表
2、逻辑函数式
3、逻辑图
4、波形图
三、逻辑函数的两种标准形式
1、最小项与最大项
最小项
最小项的性质
最大项
最大项的性质
2、最大项与最小项的关系
3、逻辑函数的最小项之和形式
4、逻辑函数的最大项之和形式
一、逻辑函数
以逻辑变量作为输入,以运算结果作为输出,那么当输入确定时,输出也就确定下来了。这是一种函数关系,称为逻辑函数,其写作Y=F(A,B,C,...)
由于该函数的输入与输出只有0/1两种状态,所以它是二值逻辑函数。
二、逻辑函数的描述方法
1、逻辑真值表
此方法不作赘述,在之前的文章已经提到多次。
2、逻辑函数式
将输入与输出之间的逻辑关系式写成与、或、非等运算的组合式,即逻辑代数式,也就得到了逻辑函数式。
例如:Y=A(B+C)
3、逻辑图
将逻辑函数式中各变量之间的与、或、非等逻辑关系用图形符号表示出来,就可以画出描述函数关系的逻辑图。
例如: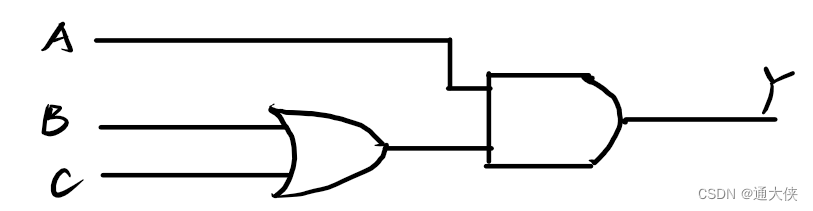
图2.1 逻辑图
4、波形图
如果将逻辑函数输入变量每一种可能出现的取值与对应的输出值按时间顺序依次排序起来,就得到了描述该逻辑函数的波形图,也称时序图。
图2.2 波形图
卡诺图与硬件描述语言后面的文章再讲。
三、逻辑函数的两种标准形式
1、最小项与最大项
最小项
在n变量逻辑函数中,若m为包含n个因子的乘积项,而且这n个变量均以原变量或反变量的形式在m中出现一次,则称m为该组变量的最小项。n变量的最小项个数有 个。
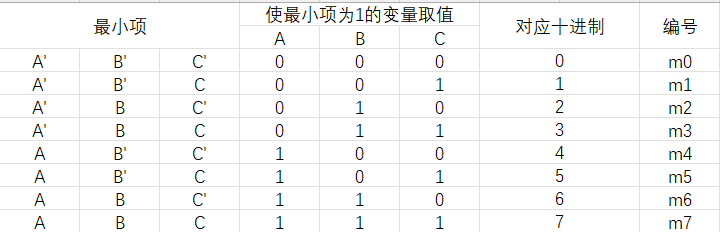
图3.1 三变量最小项的编号表
最小项是与运算,所以要使每一个因子都为1,最终值才能为1。
最小项的性质
①在输入变量的任何取值下必有一个最小项,而且仅有一个最小项的值为1;
②全体最小项之和为1;
③任意两个最小项的乘积为0;
④具有相邻性的两个最小项之和可以合并成一项并消去一对因子。
相邻性:若两个最小项只有一个因子不同,则称这两个最小项聚优品相邻性。比如A'BC'&ABC'就具有相邻性。
A'BC' + ABC' = (A+A')BC'=BC'-------------------------由公式A+A'=1得
最大项
在n变量逻辑函数中,若M为n个变量之和,而且这n个变量均以原变量或反变量的形式在M中出现一次,则称M为该组变量的最大项。

图3.2 三变量最大项的编号表
最大项的性质
①在输入变量的任何取值下必有一个最大项,而且只有一个最大项的值为0;
②全体最大项之和为0;
③任意两个最大项之和为1;
④只有一个变量不同的两个最大项的乘积等于各相同变量之和。
2、最大项与最小项的关系
3、逻辑函数的最小项之和形式
第一步:将给定的逻辑函数化成若干乘积项之和的与或形式(积之和);
第二步:利用公式A+A'=1将缺少的因子补全(凑出ABC)
例1:
也可以写作:Y(A,B,C)=Σm(3,6,7)
4、逻辑函数的最大项之和形式
第一步:将给定的逻辑函数化成若干乘积项之和的或与形式(和之积);
第二步:利用公式A·A'=0将缺少的因子补全(凑出ABC)
例2:Y=A'B+AC=(A+B+C)(A+B+C')(A'+B+C)(A'+B'+C)
也可以写作:Y(A,B,C,D)=ΠM(0,1,4,6)
若文章内容出现错误,恳请各位批评指正,感激不尽!
这篇关于数电学习笔记——逻辑函数及其描述方法的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!



