本文主要是介绍背包问题从入坑到入坟,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
闲来无事,小Z最近也是又做了几道背包问题,用来巩固自己对背包问题以及动规的理解,那么也就来写一写关于这些题的一些小小的题解
话不多说,上链接。
第一题:最大约数和

题解:一开始我还不知道啥是约数,也是小小的百度了一下,约数其实就是因子,但是不能包括自身,好了,现在我们来看这道题,还是按照咱们之前说的的动规步骤走
(1)明白dp数组的含义,dp[i]指的是第i个数的最大约数和
(2)找到状态转移方程,
dp[j]=max(dp[j],dp[j-i]+a[i]);(3)初始化,都初始化为0即可
好了现在来看AC代码:
#include<bits/stdc++.h>
using namespace std;
int s;
int a[1005];//用于统计每个数约数和为多少
int dp[1005];
int main()
{scanf("%d",&s);
for(int i=1;i<=s;i++)
{for(int j=1;j<i;j++)//不能包括本身,所以j<i;{if(i%j==0)a[i]+=j;//能被整除就加进去}
}for(int i=1;i<=s;i++){for(int j=i;j<=s;j++){dp[j]=max(dp[j],dp[j-i]+a[i]);//状态转移方程}}printf("%d",dp[s]);return 0;
}第二题:NASA的食物计划
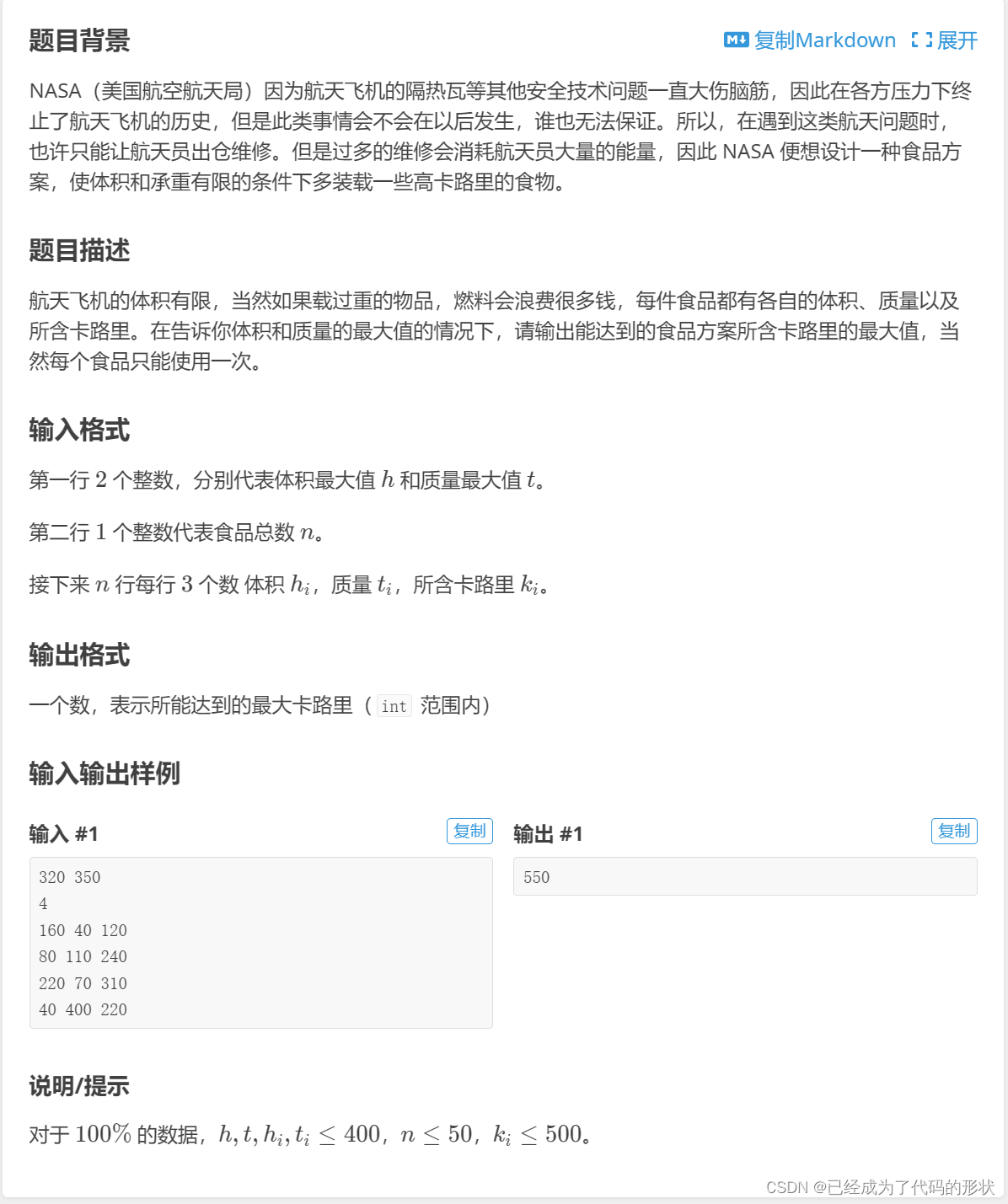
这题不像之前的背包问题,只需要考虑重量或别的一个因素,而是说要考虑两个因素,算是一种另类的背包问题吧(不要慌,遇到背包问题只需要按照我之前所说的动规五部曲,没有一道会解不出来,如果找不到状态转移方程,请当我这句话白说)
最后分析一遍,因为后续的题都和这个差不多,就变一点点。
(1)dp数组的含义,我们这里的dp[i][j]数组,指的是在体积为i,能装最大质量为j时,所能承载的最大卡路里
(2)确定dp数组的状态转移方程:
dp[j][k]=max(dp[j][k],dp[j-a[i]][k-b[i]]+c[i]);
(3)初始化:初始化为0即可,无需操作
AC代码:
#include<bits/stdc++.h>
using namespace std;
int h,t;
int n;
int a[55],b[55],c[55];//a,b,c分别代表体积,质量,卡路里
int dp[405][405];//分别代表体积和质量
int main()
{scanf("%d%d",&h,&t);scanf("%d",&n);for(int i=1;i<=n;i++){scanf("%d%d%d",&a[i],&b[i],&c[i]);}for(int i=1;i<=n;i++){for(int j=h;j>=a[i];j--){for(int k=t;k>=b[i];k--){dp[j][k]=max(dp[j][k],dp[j-a[i]][k-b[i]]+c[i]);}}}printf("%d",dp[h][t]);return 0;
}第三题:L 国的战斗之间谍

题解:和上面那个题一样,都是需要考虑两个因素
#include<bits/stdc++.h>
using namespace std;
int n,m,x;
int a[105],b[105],c[105];
int dp[1005][1005];
int main()
{scanf("%d%d%d",&n,&m,&x);for(int i=1;i<=n;i++){scanf("%d%d%d",&a[i],&b[i],&c[i]);}for(int i=1;i<=n;i++){for(int j=m;j>=b[i];j--){for(int k=x;k>=c[i];k--){dp[j][k]=max(dp[j][k],dp[j-b[i]][k-c[i]]+a[i]);}}}printf("%d",dp[m][x]);return 0;
}
第四题:榨取kkksc03
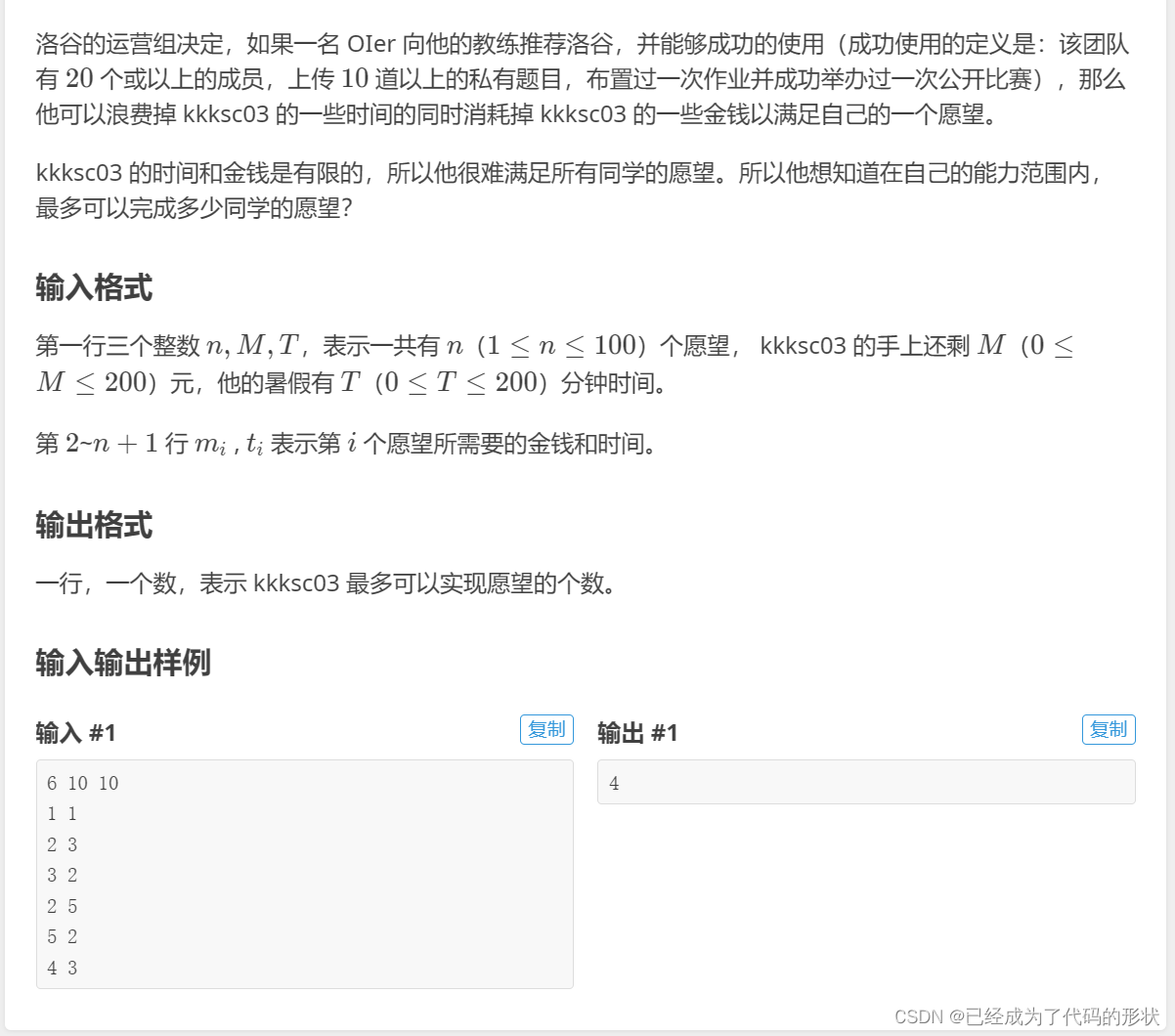
题解:一样是两个因素,只是dp数组的状态转移方程小变一下即可
#include<bits/stdc++.h>
using namespace std;
int n,m,t;
int a[105],b[105];//用于存储每个人的愿望的金钱和时间
int dp[205][205];//也是分别代表金钱和时间
int main()
{scanf("%d%d%d",&n,&m,&t);for(int i=1;i<=n;i++){scanf("%d%d",&a[i],&b[i]);}for(int i=1;i<=n;i++){for(int j=m;j>=a[i];j--){for(int k=t;k>=b[i];k--){dp[j][k]=max(dp[j][k],dp[j-a[i]][k-b[i]]+1);}}}printf("%d",dp[m][t]);return 0;
}第五题:音量调节

题解:状态转移方程改变一下即可
if(dp[i-1][j]==1&&j+a[i]<=max1)
dp[i][j+a[i]]=1;
if(dp[i-1][j]==1&&j-a[i]>=0)
dp[i][j-a[i]]=1;
AC代码:
#include<bits/stdc++.h>
using namespace std;int n,start,max1;
int a[55];
int dp[55][1005];
int main()
{scanf("%d%d%d",&n,&start,&max1);dp[0][start]=1;for(int i=1;i<=n;i++){scanf("%d",&a[i]);}for(int i=1;i<=n;i++){for(int j=0;j<=max1;j++){if(dp[i-1][j]==1&&j+a[i]<=max1)dp[i][j+a[i]]=1;if(dp[i-1][j]==1&&j-a[i]>=0)dp[i][j-a[i]]=1;}}for(int i=max1;i>=0;i--){if(dp[n][i]==1){printf("%d",i);return 0;}}printf("-1");return 0;
}
这篇关于背包问题从入坑到入坟的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






