codeforces (#622 Div2) 1393D Rarity and New Dress

本文主要是介绍codeforces (#622 Div2) 1393D Rarity and New Dress，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

题目链接：
https://codeforces.com/contest/1393/problem/D
题目大意：
给出一个由字符串组成的矩阵，寻找其中有多少个相同字母组成的菱形（旋转45度的正方形）。
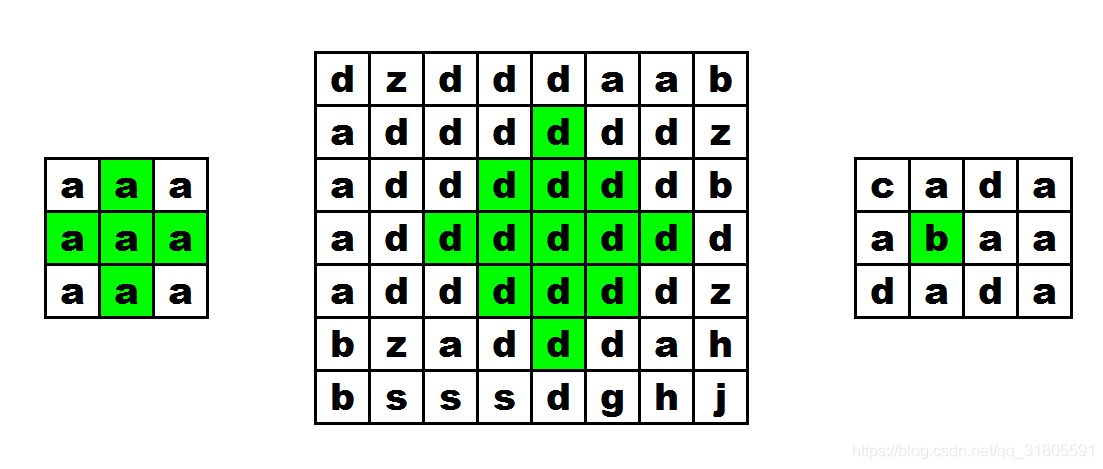
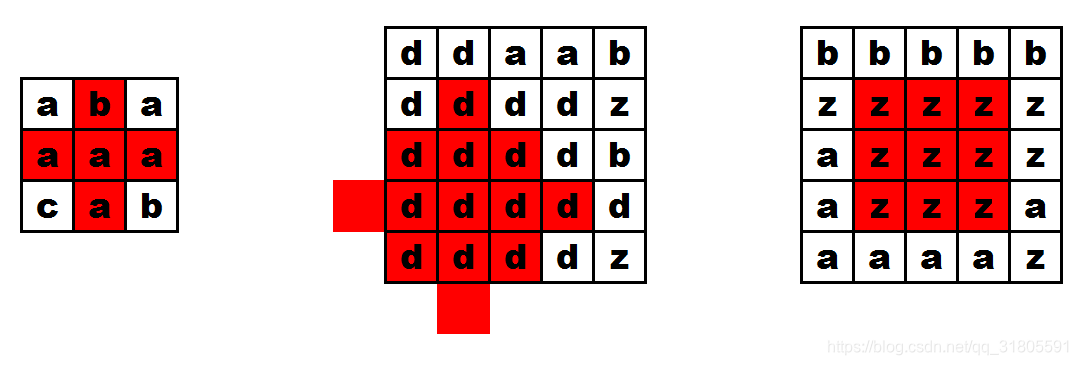
在这里插入图片描述

如图，绿色的可以，红色的不行。

输入：
5 5
zbacg
baaac
aaaaa
eaaad
weadd
输出：
31

题解：
这道题其实个人觉得比这场比赛的c题简单。
首先，我们先对于同种字符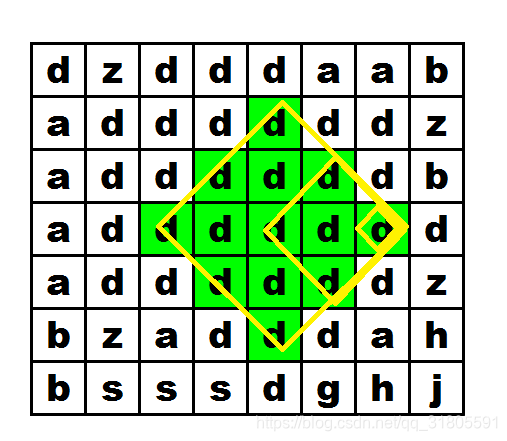，在这里插入图片描述
我们先取菱形的最右端的点，看他最大能组成多大的菱形，那么同样以其为菱形最右端的点，其肯定也能构成更小的菱形。那如图，要构成大小为3（边长）的菱形，那么红色的点的相同的前缀必须为5，且蓝色点的相同字符前缀必须为3，紫色的为1：
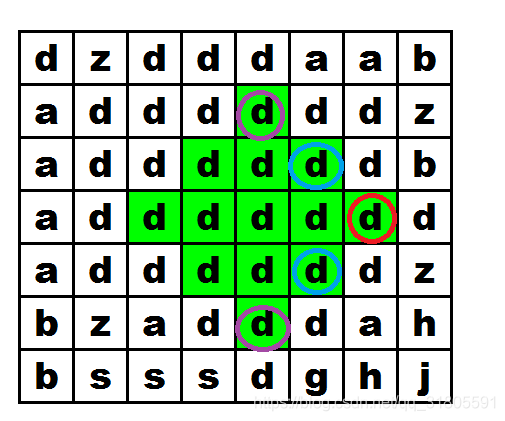
在这里插入图片描述
那么推广一下，可发现，红色的点形成的最大菱形受（左斜上方的连续前缀的增长长度，和右下方的连续前缀增长长度，红色点的连续前缀长度）限制。
于是我们可以把一个菱形先分成上下两个部分；
如图，黑色是已经能形成的最大菱形的上半部分，红色是该点的前缀，蓝色是改点能形成的最大菱形的上半部分。
在这里插入图片描述

mxLevel[ii][jj] = min(mxLevel[ii - 1][jj - 1] + 1, toLevel(ii, jj));
myLevel[ii][jj] = min(myLevel[ii + 1][jj - 1] + 1, toLevel(ii, jj));
res += min(mxLevel[i][j], myLevel[i][j]);
//mxLevel 保存的是改点与其左上方连续能形成的最大菱形的上半部分
//myLevel 保存的是改点与其右下方连续能形成的最大菱形的下半部分
//toLevel 是获得该点连续前缀长度可以形成的最大边长
//res 是统计最终答案

最终代码：

#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int maxn = 2005;char mx[maxn][maxn];
int n, m;
int mxLevel[maxn][maxn];
int myLevel[maxn][maxn];
int sm[maxn][maxn];inline int toLevel(int ii, int jj)
{return (sm[ii][jj] + 1) / 2;
}int main()
{scanf("%d%d", &n, &m);for (int i = 1; i <= n; i++)scanf("%s", &mx[i][1]);for (int i = 1; i <= n; i++) {for (int j = 1; j <= m; j++) {sm[i][j] = (mx[i][j] == mx[i][j - 1] ? sm[i][j - 1] + 1 : 1);}}for (int i = 1, j = m; i <= n;) {int ii = i, jj = j;while (ii <= n && jj <= m) {if (mx[ii][jj] == mx[ii - 1][jj - 1])mxLevel[ii][jj] = min(mxLevel[ii - 1][jj - 1] + 1, toLevel(ii, jj));elsemxLevel[ii][jj] = 1;ii++, jj++;}if (j > 1) j--;else i++;}for (int i = n, j = m; i >= 1;) {int ii = i, jj = j;while (ii >= 1 && jj <= m) {if (mx[ii][jj] == mx[ii + 1][jj - 1])myLevel[ii][jj] = min(myLevel[ii + 1][jj - 1] + 1, toLevel(ii, jj));elsemyLevel[ii][jj] = 1;ii--, jj++;}if (j > 1) j--;else i--;}int res = 0;for (int i = 1; i <= n; i++) {for (int j = 1; j <= m; j++) {res += min(mxLevel[i][j], myLevel[i][j]);//printf("mxL[%d][%d]=%d myL=%d\n", i, j, mxLevel[i][j], myLevel[i][j]);}}printf("%d\n", res);return 0;
}