本文主要是介绍排序算法——朝花夕拾,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
1 冒泡排序
1-1 思路
冒泡排序说实话我还挺烦的,虽然说是最简单的排序算法,但我还真没把握一次就写出来,因为距离上一次写冒泡排序还是在4年前。而且冒泡的细节还是比较多的。
冒泡排序的思想主要就是一个个比较,先确定最后一个元素,再确定倒数第二个元素。记也比较好记,外层循环是,循环的次数,没有任何逻辑在里面,内层循环是控制冒泡。
首先,10个元素要循环9次才能确定位置,因此外层的循环次数是 n-1。
for (int i=1; i<len; ++i) {}
为什么是 1~n-1 而不是 0~n-1 呢?因此,第一次循环需要9次,第二次循环就需要8次,可以发现第 n 次循环与 需要的次数 m 互补, n + m = 10。这样内层循环可以写成len-i 而不是 len-i-1 比较好看。
for (int i=1; i<len; ++i) {for (int j=0; j<len-i; ++j) {}
}
然后是冒泡,冒泡是以过程为核心的,而不是一个元素为核心的,每次冒泡都是从第一个位置的元素开始,一直与下一个位置的元素比较,如果大于就交换,注意这里为什么要把位置加粗,因为,很多新手在写的时候,以为是以元素为核心的,当遇到冒泡不下去的时候就停止本轮循环,这是不对的,要一直比完,每一轮循环都会确定一个最后的元素。因此内层循环是从 j 开始 到 len-i 结束,比较的是 j 与 j+1,且 j 每次都是从0 开始。
for (int i=1; i<len; ++i) {for (int j=0; j<len-i; ++j) {temp = arr[j];arr[j] = arr[j+1];arr[j+1] = temp;}
}
1-2 代码实现
let arr = [49, 38, 65, 97, 76, 13, 27, 49];function popSort(arr) {let len = arr.length, temp;let newArr = [...arr];for (let i=1; i<len; ++i) {for (let j=0; j<len-i; ++j) {if (newArr[j] > newArr[j+1]) {temp = newArr[j+1];newArr[j+1] = newArr[j];newArr[j] = temp;}}}return newArr;
}console.log(popSort(arr));
1-3 稳定性
稳定。
可以看到,最内层的 if 语句是大于小于号,而没有等于在里面,因此当原数组的元素在冒泡的过程中遇到相同的元素,是不会继续交换位置的,因此是稳定的。
2 快速排序
2-1 思路
思路就是在一组数据中选取一个中间大小的轴枢元素 pivot,然后对整个数组进行划分,把比 pivot小的元素划分到pivot左边,把大的划分到右边。这样pivot 的位置就已经固定了,然后递归地划分pivot的左侧和右侧,视为一个一模一样的子问题,直到全部解决。
具体实现细节可以使用双指针,分别指向数组的两头,保存最左侧的值,然后开始循环,具体见代码实现部分。
2-2 代码实现
而且注意这里直接选取
lo作为 轴枢 是不合理的,具体的理由以及优化手段见 OI WIKI 中快速排序部分。
这里要注意,函数参数中的 low 和 high 不能在函数内部直接使用,要复制它的 lo, hi 作为拷贝使用,否则在递归时,关于边界将无法处理。
关于内层的两个 while 中的第二个判断条件,一定要用 >= and <=,因为假设给你数据 [3,1,4,2,5,2 3] 进行排序,两头的元素一致,你直接就死循环了。
let arr = [49, 38, 65, 97, 76, 13, 27, 49];function quickSort(arr, low = 0 ,high = arr.length - 1) {let lo = low, hi = high;if (lo >= hi) return;let pivot = arr[lo];while (lo < hi) {// 遇到比pivot大的,hi停止,并赋值给arr[lo],arr[lo] 已经在上面保存过了while (lo < hi && arr[hi] >= pivot) hi --;arr[lo] = arr[hi];// 遇到比pivot小的,lo停止,并赋值给arr[hi]while (lo < hi && arr[lo] <= pivot) lo ++;arr[hi] = arr[lo];}// 当while结束后,恢复pivot信息arr[lo] = pivot;quickSort(arr, low, lo - 1);quickSort(arr, lo + 1, high);return arr;
}console.log(quickSort(arr));
2-3 优化思路
关于稳定性以及为什么算法会退化的讨论。
上面的文章简要提到了算法目前的不足。算法的理想最优情况下是:每次找到的 pivot元素的下标 在一轮划分后,刚好处于数组最中间的位置。
考虑一个很差的情况,不论数组是 [1,1,1,1,1,1,1] 还是 [1,2,3,4,5,6,7],长度设为 n ,在我上面给出的代码中,内部的第一个while循环会直接把 hi 拉到 lo 的位置,进行一次交换后,一轮划分完成后,下一次待划分的部分的长度将是 n-1,这样的时间复杂度很容易理解,将会是 n*(n-1)*(n-2)* ... *1退化到 O(n^2) 的复杂度。
完整优化策略:见 OI WIKI 中快速排序部分。
这里我细说一个优化策略,就是在待排序部分选择 arr[lo], arr[mid], arr[hi] 三者中中间的那个数作为轴枢元素,然后和 arr[lo] 进行交换,最后再执行后面的循环。
例如:1, 4, 3, 6, 2, 7,如果我们始终选 arr[lo] 作为轴枢元素,那么我们第一次就会选到 1 ,划分后的数组不变,这样就会发生我们上面提到的退化。
如果我们在这里执行上面的优化手段。arr[lo] = 1, arr[mid] = 3, arr[hi] = 7 ,数组在交换后为 3, 4, 1, 6, 2, 7 ,在一轮划分后为 2, 1, 3, 6, 4 ,7, 这样左边的长度为2,右边的长度为3,就更接近于最理想的情况。
while (lo < hi) {int num1 = nums[lo],num2 = nums[(lo + hi) / 2],num3 = nums[hi],swapPivot = lo;if ((num1 <= num2 && num2 <= num3) || (num3 <= num2 && num2 <= num1)) {swapPivot = (lo + hi) / 2;} else if ((num1 <= num3 && num3 <= num2) || (num2 <= num3 && num3 <= num1)) {wapPivot = hi;}swap(nums[swapPivot], nums[lo]);...
}
2-4 JavaScript中代码级别的优化
我们尽量这里做一个纯函数,一个函数的返回结果只依赖其参数,并且执行过程中没有副作用。
因此我们将代码做一些小小的改动
let arr = [49, 38, 65, 97, 76, 13, 27, 49];function quickSort(arr, low = 0 ,high = arr.length - 1) {const sort = function (arr, low, high) {let lo = low, hi = high;if (lo >= hi) return;let pivot = arr[lo];while (lo < hi) {while (lo < hi && arr[hi] >= pivot) hi --;arr[lo] = arr[hi];while (lo < hi && arr[lo] <= pivot) lo ++;arr[hi] = arr[lo];}arr[lo] = pivot;sort(arr, low, lo - 1);sort(arr, lo + 1, high);return arr;}newArr = arr.concat()return sort(newArr, low, high);
}console.log(quickSort(arr));
2-5 稳定性
这个很容易看出来,快速排序使用的是交换,而不是插入,因此是不稳定,但我觉得如果使用额外的空间,还是可以使其变得稳定的。
选择排序
思路
整体来说维护一个空的序列(已排序序列)和一个未排序序列,在一开始的时候未排序的序列为数组本身,先在未排序序列中选择一个最小的元素,与未排序序列队头元素进行交换,并把该元素从未排序序列中移除,加入已排序序列。重复此过程。
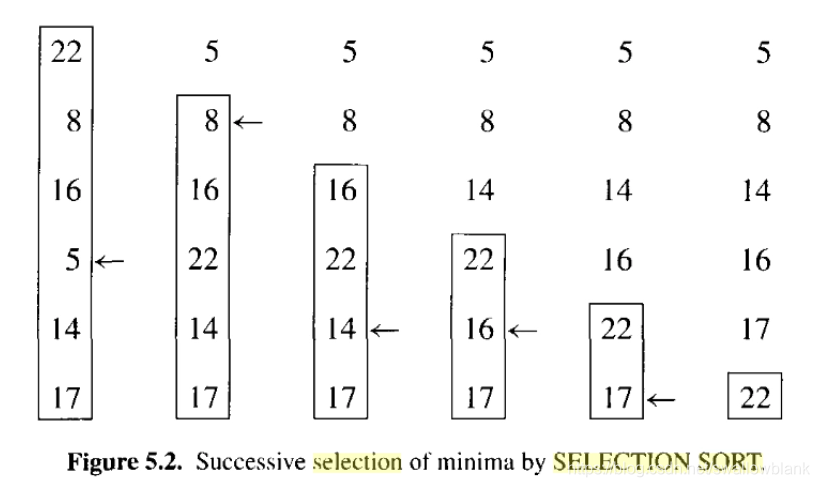

代码实现
let arr= [3,2,5,1,5,6,7];function selectSort(arr) {let len = arr.length;for (let i=0; i<len-1; i++) {let minIdx = i;for (let j=i+1; j<len; j++) {if (arr[j] < arr[minIdx]) {minIdx = j;}}let temp = arr[i];arr[i] = arr[minIdx];arr[minIdx] = temp;}return arr;
}console.log(selectSort(arr));
插入排序
思路
插入排序与选择排序相反,选择排序是在未排序的数组中选出一个数放入已排序数组,而插入排序是拿出第一个未排序数组中的数逐个与已排序数组中的数比较,若小于,就交换位置,直到大于。
代码实现
let arr= [3,2,5,1,5,6,7];function insertSort(arr) {let len = arr.length;for (let i=1; i<len; i++) {let j = i;for (let j=i; j>0; j--) {if (arr[j] < arr[j-1]) {let temp = arr[j-1];arr[j-1] = arr[j];arr[j] = temp;}}}return arr;
}console.log(insertSort(arr));
总结
关于稳定性
| 算法 | 稳定性 |
|---|---|
| 选择 | 不稳定,因为要交换 |
| 快速 | 不稳定,因为要交换 |
| 堆排 | 不稳定 |
| 希尔 | 不稳定 |
| 冒泡 | 稳定,因为是逐个比较,当相等时不进行操作,不会破坏原有结构 |
| 插入 | 稳定,因为是逐个比较 |
| 归并 | 稳定 |
| 基数 | 稳定 |
这篇关于排序算法——朝花夕拾的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






