树的括号表示法

2024-02-28 19:52
文章标签 括号 表示法

本文主要是介绍树的括号表示法，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

1.括号表示法构造一棵树

下面的代码都使用下面的图测试：
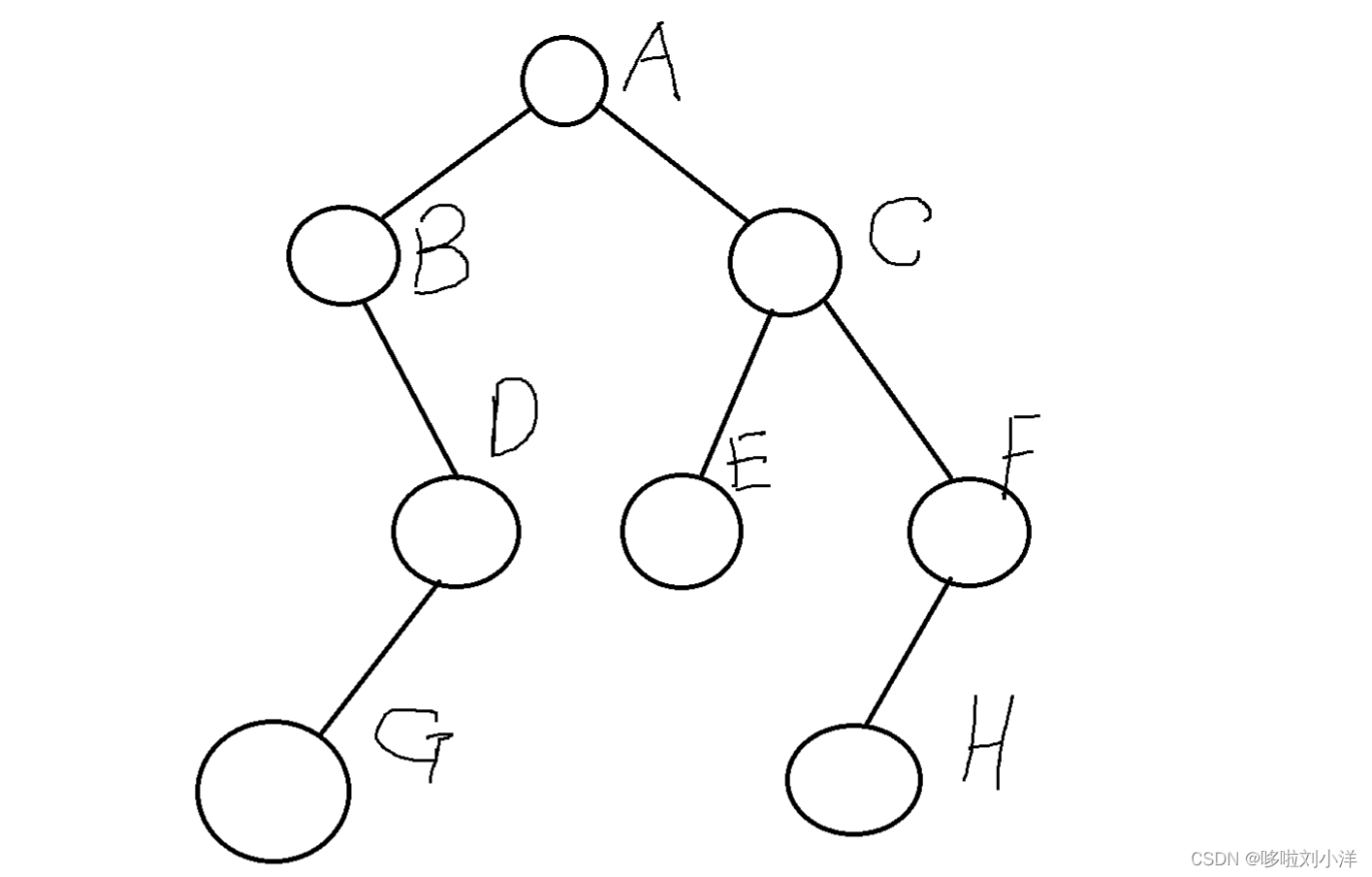
在这里插入图片描述

这颗树的前序遍历是

  • [A,B,D,G,C,E,F,H]

为了程序的完整性，我想先构建一颗上述树，知识匮乏的我只能使用括号表示法构造:

  • “A(B(,D(G,)),C(E,F(H,)))”

1.用一个类表示树的节点

class Node 
{
public:int val;vector<Node*> children;   //每个Node节点包含一个children数组，数组元素是Node*类型，表示指向其它的节点//三个构造函数Node() {} Node(int _val) {val = _val;}Node(int _val, vector<Node*> _children) {val = _val;children = _children;}
};

2.使用括号表示法构建树

void CreateTree(Node *&root,string &s)
{stack<Node*>tree;Node* p = NULL;int i =0;char ch = s[0];while (i < s.length()){switch (ch){case '(':tree.push(p);break;case ')':tree.pop();break;case ',':break;default:p = new Node();p->val = ch;if (root == NULL)  //没有加入根节点{root = p;}else{tree.top()->children.push_back(p);}}ch = s[++i];}
}

我觉得这个代码逻辑非常清晰，我想尝试一下用递归的方式完成上述代码。在此之前，我先介绍一下我现在对于构建二叉树的理解,我感觉这个难度不亚于用非递归写出树的前中后序遍历😋

个人见解:
对于S字符串分析，S=A(B(,D(G,)),C(E,F(H,)))。从头开始遍历，想要通过S字符串构建一颗树。
想要将问题给解决，必须找到字符串内在的联系并且将其具体化。发现，所有的括号都是配对出现的，且’(‘其配对的是最近的’）’。每次当遇到’(‘的时候，可以把新的问题具体成”构建一棵小树“（发现和最开始的问题是一个内在逻辑）。然后小树挂在大树身上
解释一下：
最开始的问题是构建A(B(,D(G,)),C(E,F(H,))) 这棵树。
遍历到B后面的’(‘的时候，问题变成构建B(,D(G,)),C(E,F(H,))这棵树，然后B挂在A身上
遍历到D后面的’(‘的时候，问题变成构建D(G,)这颗树。然后D挂在B身上
发现了实际上就是解决无数个这样的小问题最后解决大问题，而进入小问题的接口就是遇到’('。所以只需要能解决最简单的A(B,C)这个问题，那么后面无限的衍生都是一个道理。
问题即抽象为：
A ( B , C , D , E . . . . ) A(B,C,D,E....) A(B,C,D,E....)
即将每个子树都‘挂’在A后面即可

Node* CreateTree1(int i,int len) //表示创建一颗树(从下标i(根节点）开始，后面跟着长度为len的子树）即用s[i]~s[i+len]构造树
{if (s[i] == ',')return NULL;  //树的根应该是一个字母Node* p = new Node();p->val = s[i];if (len == 0)return p;//接下来要把该根节点的所有子树都挂在它身上//要创建若干颗树//子树都是由字符串s构造的int start = i + 2;  //子树开始位置int length = 0;   //子树(除去根节点)长度(从根节点后面第一个左括号到匹配完所有对应的右括号为止）比如A(B(C,D),E),这里面B(C,D)就是一个子树，子树长度在这里指根节点后面跟着的长度+1，即(C,D)的长度为5,B(C,D)的长度是6while (start <= i+len)// 子树的区间[i+2,i+len],s[i+2]是子树的根节点{if (s[start] < 'A'|| s[start]>'Z') //保证s[start]是个字母（树的根节点）{start++;continue; }length = Find_BabyTree(start);  //找子树长度p->children.push_back(CreateTree1(start, length));  //子树挂到根节点后面start = start + length + 2;  //下一个子树的起点}return p;
}
我的测试数据A(B(,D(G,)),C(E,F(H,)))
输出是正确的，就是博客开头的树

放完整代码

#include<iostream>
#include<vector>
#include<cstring>
#include<new>
#include<stack>using namespace std;class Node
{
public:int val;vector<Node*> children;   //每个Node节点包含一个children数组，数组元素是Node*类型，表示指向其它的节点//三个构造函数Node() {}Node(int _val){val = _val;}Node(int _val, vector<Node*> _children){val = _val;children = _children;}
};string s;void CreateTree(Node*& root, string& s)  //括号表示法构建树，非递归法
{stack<Node*>tree;Node* p = NULL;int i = 0;char ch = s[0];while (i < s.length()){switch (ch){case '(':tree.push(p);break;case ')':tree.pop();break;case ',':break;default:p = new Node();p->val = ch;if (root == NULL)  //没有加入根节点{root = p;}else{tree.top()->children.push_back(p);}}ch = s[++i];}}void preOrdered(Node* root)  //前序遍历，非递归法
{if (root == NULL)return;cout << char(root->val) << " ";for (int i = 0; i < root->children.size(); i++)preOrdered(root->children[i]);return;
}int Find_BabyTree(int start)  //数以s[start]为根节点的子树长度
{//根据括号规律，一个'('匹配一个')'，当'('的次数等于')'的次数时表示当前这颗树构造完了//左括号+1，右括号-1if (s[start + 1] !='(')return  0;  //该树只有一个根节点,子树长度为0int kuohao = 0;int i = 1;for (i; i + start < s.length(); i++){if (s[start+i] == '(')kuohao++;if (s[start+i] == ')')kuohao--;if (kuohao == 0)break;}return i;
}Node* CreateTree1(int i,int len) //表示创建一颗树(从下标i(根节点）开始，后面跟着长度为len的子树）即用s[i]~s[i+len]构造树
{if (s[i] == ',')return NULL;  //树的根应该是一个字母个Node* p = new Node();p->val = s[i];if (len == 0)return p;//接下来要把该根节点的所有子树都挂在它身上//要创建若干颗树//子树都是由字符串s构造的int start = i + 2;  //子树开始位置int length = 0;   //子树长度(从根节点后面第一个左括号到匹配完所有对应的右括号为止）比如A(B(C,D),E),这里面B(C,D)就是一个子树，子树长度在这里指根节点后面跟着的长度，即(B,C)的长度为5while (start <= i+len)// 子树的区间[i+2,i+len],s[i+2]是子树的根节点{if (s[start] < 'A'|| s[start]>'Z') //保证s[start]是个字母（树的根节点）{start++;continue; }length = Find_BabyTree(start);  //找子树长度p->children.push_back(CreateTree1(start, length));  //子树挂到根节点后面start = start + length + 2;  //下一个子树的起点}return p;
}int main()
{Node* root = NULL;  //根节点s = "A(B(,D(G,)),C(E,F(H,)))";  //使用括号表示法构建树//CreateTree(root, s);  //建树root = CreateTree1(0,s.length()-1);//然后用前序遍历输出树看是否正确preOrdered(root);  //前序遍历return 0;
}

强迫症使然，找到思考大致的题目：leetcode
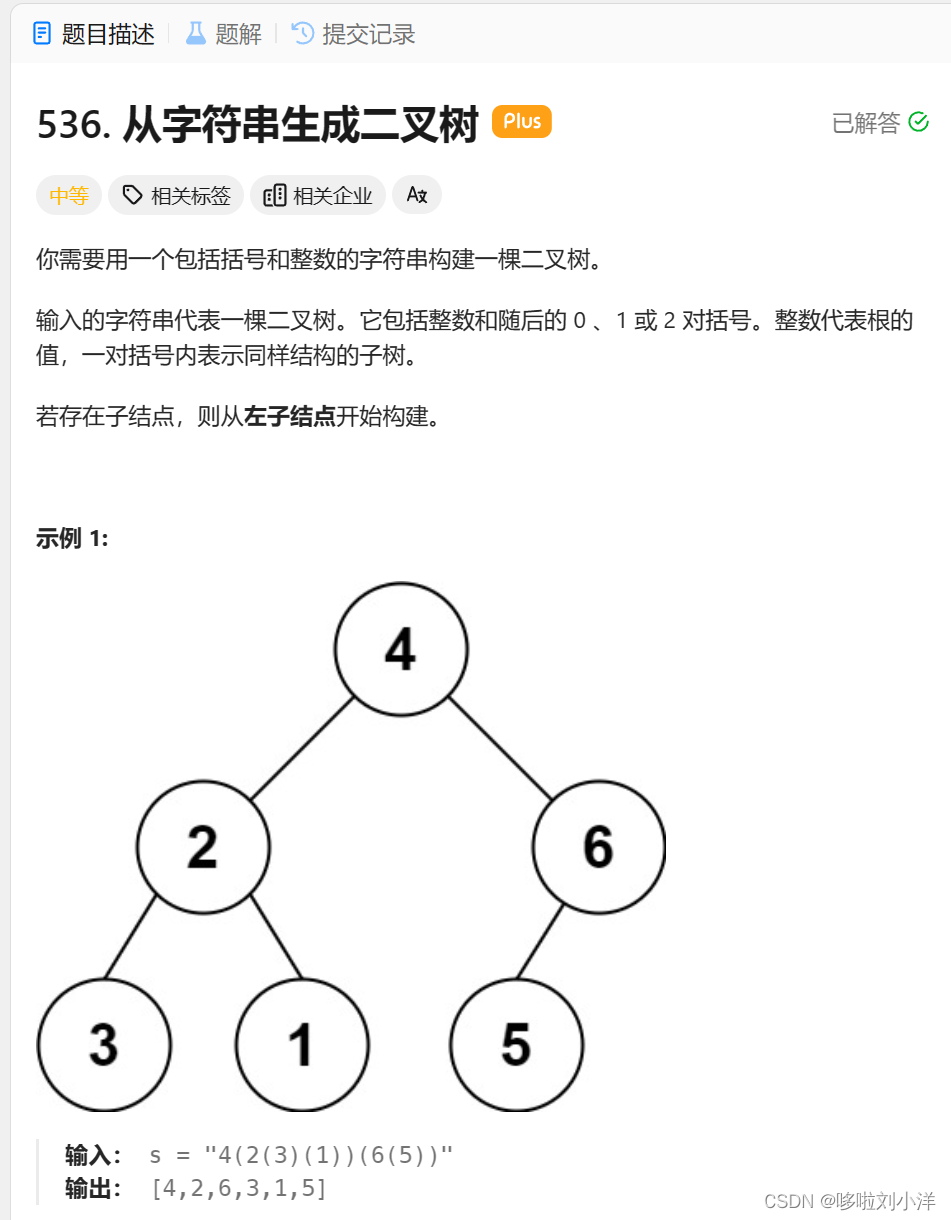
在这里插入图片描述

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution 
{
public:TreeNode* CreateTree(string s)  //表示当前根节点是s[i],当前的树的长度是len（包括i）{if(!s.size())return NULL;TreeNode*root=new TreeNode();int flag=1;int i=0;if(s[i]=='-')  //特殊判断负数{flag=-flag;i++;}//要将截至到最近的'('的所有字符提取出来转换为数字（有可能不是一个字符）int st=i;int n=s.size();while(i<n&&s[i]!='(')i++;root->val=flag*stoi(s.substr(st,i));if(i==n)return root; //只有数字没有括号的情况，可以提前退出//处理子树int kuohao=1;   //此时i指向左括号，左括号数量加1int ls=i+1;i++;for(;i<n&&kuohao!=0;i++){if(s[i]=='(')kuohao++;if(s[i]==')')kuohao--;}//此时k指向左子树结束的后一个字符root->left=str2tree(s.substr(ls,i-ls-1));//看是否有右子树if(i<n){root->right=str2tree(s.substr(i+1,n-i-2));  //有点难算，先画个图}return root;}TreeNode* str2tree(string s) {//分解问题，找到规律：//遇到字符则新建节点（当成一颗新树）//将当前字符为根节点的左右子树挂到根节点后面（左右子树）TreeNode *root=NULL;root=CreateTree(s);return root;}
};

这篇关于树的括号表示法的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/756454。

相关文章

括号匹配问题（nyoj2）

括号匹配问题（nyoj2）

括号配对问题 时间限制： 3000 ms  |  内存限制： 65535 KB 难度： 3 描述 现在，有一行括号序列，请你检查这行括号是否配对。 输入 第一行输入一个数N（0<N<=100）,表示有N组测试数据。后面的N行输入多组输入数据，每组输入数据都是一个字符串S(S的长度小于10000，且S不是空串），测试数据组数少于5组。数据保证S中只含有"[","]","(",")"
阅读更多...
VSC++： 括号对称比较

VSC++： 括号对称比较

括号的使用规则：大括号，中括号，小括号{[()]}；中括号，小括号[()]；小括号()；大括号、中括号、小括号、中括号、小括号、大括号{[()][()]}；大括号，中括号，小括号，小括号{[(())]}；大括号，中括号，小括号，小括号{[()()]}；小括号不能嵌套，小括号可连续使用。 {[]}、{()}、([])、({})、[{}]、{}、[]、{[}]、[(])都属非法。 char aa[
阅读更多...
vim 括号匹配 以及各种好用跳转技巧

vim 括号匹配 以及各种好用跳转技巧

括号匹配: % 可以让光标从它当前所在的括号跳转到与它相匹配的括号上去, 对花括号和 圆括号, 方括号都有效, 常用于手工检查括号是否匹对. 标示位置 -------- 你可以在档案□做些标记再随时返回被标记的位置. m char (MARK) 把这个地方标示成 char ' char (quote character) 跳到被标为 char的
阅读更多...
vim匹配括号之间内容

vim匹配括号之间内容

示例代码如下： var tpl = ['<a href="{url}">{title}</a>'] 我们想要找到{url}之间的内容 光标移动至 {url}，输入vi{ 分隔符对象 文本对象选择区域a) 或 ab一对圆括号 (parentheses)i) 或 ib圆括号 (parentheses) 内部a} 或 aB一对花括号 {braces}i} 或 iB花括号 {braces}
阅读更多...
sublime text3按tab键跳出括号、双引号设置

sublime text3按tab键跳出括号、双引号设置

直接在Preferences->Key Bindings中文界面为首选项->快捷键设置中添加下列代码： { "keys": ["tab"], "command": "move", "args": {"by": "characters", "forward": true}, "context":[{ "key": "following_text", "operator": "regex_conta
阅读更多...
Leetcode22括号生成(java实现)

Leetcode22括号生成(java实现)

今天分享的题目是Leetcode22括号生成，具体的题目描述如下： 本道题我们使用的解法是回溯。 解题思路： 我们主要是对括号出现的可能性进行一个收集。 我们以n=2举例子，如下图 如果想要合法，那么一定是左括号开始，并且以左括号为开始，要对不合适的进行剔除。可以思考一下，为何最后一个不符合呢？是因为左括号个数为1，右括号个数为1，然后没有以左括号开始。 上面的两种情况合法，第一种情况，左括
阅读更多...
22括号生成

22括号生成

看题目描述 这样的话，首先返回的东西是一个列表<String> 看到有关括号匹配括号生成我们自然而然想到了，栈 Stack<Character> n>=1 <=8所以我们不需要考虑栈为空的可能 那么思路如下，如果括号是左括号，丢进去，然后如果是又括号，那么就要考虑前面，那么可以用到stack的push和pop方法 首先它题目里面只给我们一个n然后那么我们栈空间需要2n 然后所有可能也就是我们需
阅读更多...
算法---------括号生成

算法---------括号生成

题目： 给出 n 代表生成括号的对数，请你写出一个函数，使其能够生成所有可能的并且有效的括号组合。例如，给出 n = 3，生成结果为：["((()))","(()())","(())()","()(())","()()()"]来源：力扣（LeetCode）链接：https://leetcode-cn.com/problems/generate-parentheses著作权归领扣网络所有。商
阅读更多...
Java：有效括号字符串验证器

Java：有效括号字符串验证器

Java实现的有效括号字符串验证器 引言 在编程中，经常需要验证一组字符串中的括号是否正确配对。例如，检查一段代码或表达式中的圆括号、方括号和花括号是否成对出现。这类问题不仅在编程语言解析器中非常重要，也是许多软件开发场景中的基础需求。本文将介绍一种基于Java语言实现的有效括号字符串验证器，并通过JUnit框架对其进行测试。 问题描述 给定一个只包含 '(', ')', '{', '}'
阅读更多...
32力扣 最长有效括号

32力扣 最长有效括号

dp方法： class Solution {public:int longestValidParentheses(string s) {int n=s.size();vector<int> dp(n,0);if(n==0 || n==1) return 0;if(s[0]=='(' && s[1]==')'){dp[1]=2;}for(int i=2;i<n;i++){if(s[i]=='
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2