本文主要是介绍摆线轮基础,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
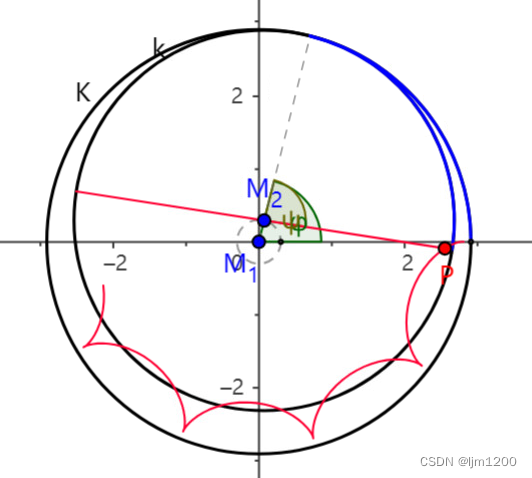
摆线是圆滚动过程中,上面一个固定点运动的轨迹。Cycloid”一词,及其形容词“Cycloidal”,源自“Hypocycloid”这一词汇,它描述了一个小圆的圆周上的一个点在一个较大的固定圆周上旋转所形成的曲线,即摆线轮曲线。
首先来推导一下摆线方程,假设点P从O点运动到现在的位置,红色弧线长度应该等于下面横线的长度。那么P点的坐标(x,y)

设a为滚圆半径
在X轴上at 圆心移动距离(弧度长度)asint是圆上的点的相对于圆心的调整,在Y轴上a 圆心移动距离,acost 圆上的点的相对于圆心的调整。
为了更直观的表达,半径用字母R表示,转动过的角度用字母θ表示,那么整理后的方程为
继续推导摆线轮方程,摆线轮曲线是滚圆在基圆上滚动一周形成的轨迹:
基圆的方程为
那滚动圆的圆心轨迹方程为
在推到摆线轮方程之前,我们先说说具有收缩摆线的摆线轮。直接用滚圆摆线轮具有相对较高的偏心率,导致高速下产生巨大的不平衡力,并导致不平稳的运行。大偏心距还导致摆线轮中的柱销孔径相对较大,因此彼此靠近。孔之间的材料厚度较低可能会导致在受到高压力时孔的变形。出于这些原因,摆线轮通常采用所谓的收缩摆线。绘制点不再放置在滚动圆的周长上(距离 R),而是位于滚动圆内部(距离 r < R)。相比之下,如果绘制点放置在滚动圆外部(距离 r >R),则得到扩展的摆线。然而,在机械工程中,后者毫无意义,因此只使用收缩摆线


推导收缩摆线轮公式:

由于滚动过的弧长相等
把坐标用 表示出来
那么摆线轮的方程为:
如果是内摆线
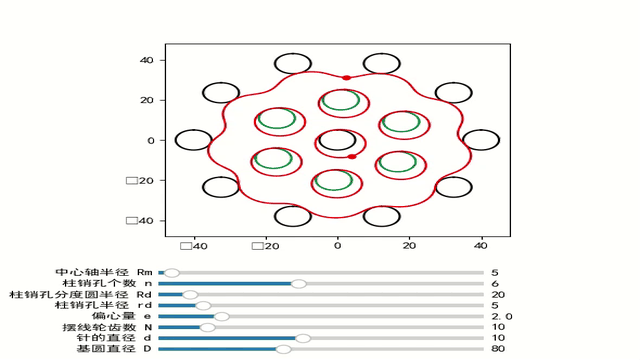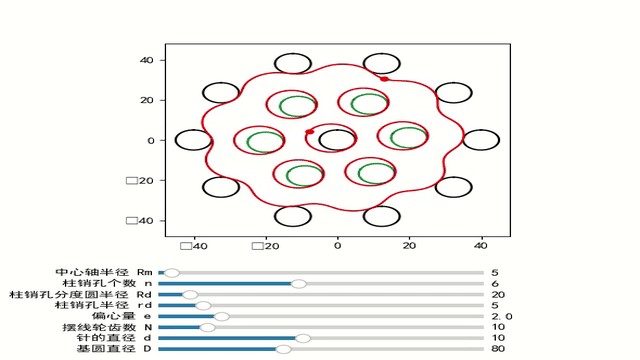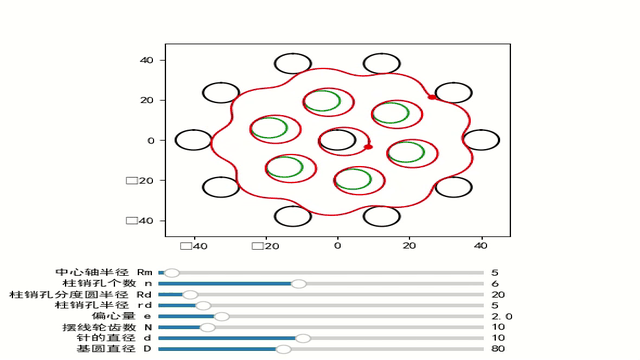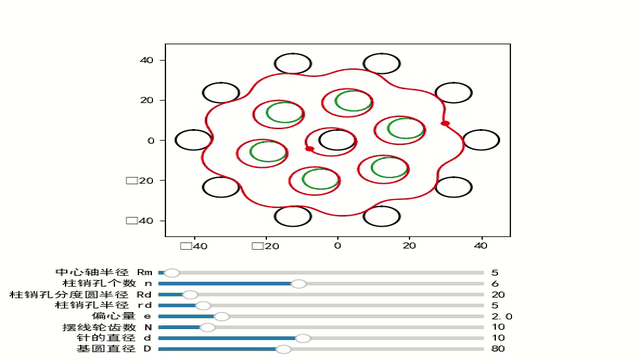
这篇关于摆线轮基础的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





