长期气象站资料的均一化订正——以最大风速为例

气候序列中某些时段由于非自然原因造成的系统偏差，非自然原因包括台站迁移、观测规则/仪器改变、卫星更替等。非均一性可扭曲气候变化及其影响的定量评估，也会影响气候变化的归因研究。均一化即检测和校订时间序列中的非均一性。事实上，几乎所有长期气象观测序列都混杂有多种非均一性，难以通过特定物理校订进行全面的均一化（引自大气所严中伟老师的教学ppt）。

PS: 非均一性，即认为两段数据之间的统计特征不一致了，比如均值和方差不同。假如数据符合正太分布，如果均值和方差不同，那么就可以认为这两段数据不属于一个分布。

自 20 世纪 80 年初期开始，随着改革开放以后城市化进程逐渐加快，各气象站周围观测环境发生了一些变化，使得风速的观测值明显减小，影响风速资料的均一性，因此需要对气象站长年代的风速资料进行均一性检验，并对非均一性的风速资料进行均一性订正，去除城市化的影响。

以广东省阳江市1971年至2015年的年最大风速为例，进行订正。检测到了1986年有一个转折，对应改革开放以后发展较快，城市化进程影响了气象站最大风速。该站2003年以后搬迁，因此我们只订正2003年之前的。订正后的数据和订正前还是有明显的区别，可想而知，如果不做订正，那么使用该资料进行其他用途会有一个比较大的偏差，比如计算重现期，对各种工程设计影响还是比较大的。

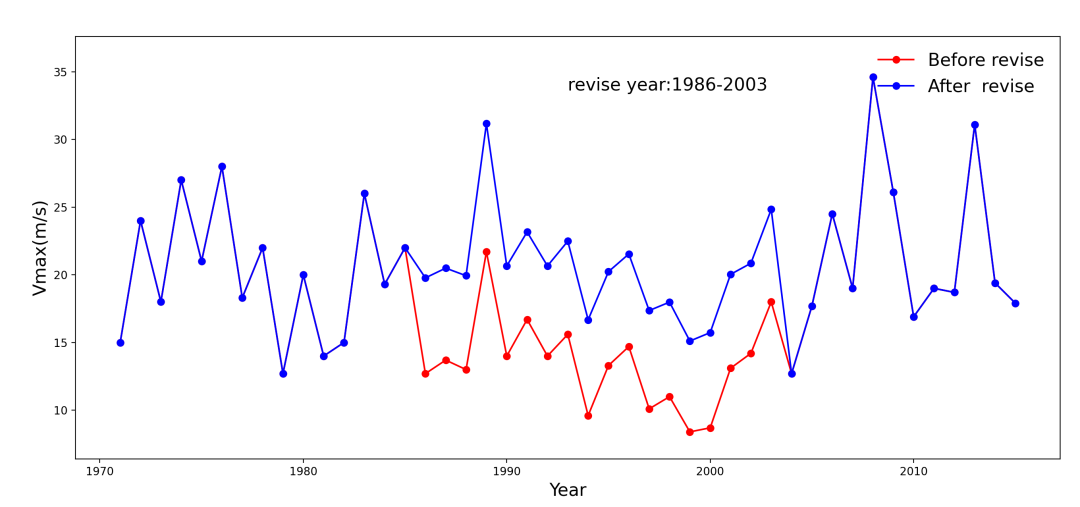
阳江气象站年最大风速订正

具体方法

首先检测各台站风速资料的均一性，找到转折年，具体方法如下：对风速序列资料，滑动选取某一年作为转折年，将该年的之前（不包括该年）的风速序列称为子序列X1，长度为n1，其后的子序列为X2，长度为n2。全部数据的均值为，序列X1和X2的均值为和，于是有：

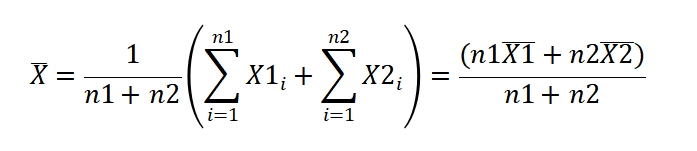
全部数据的偏差平方和为：

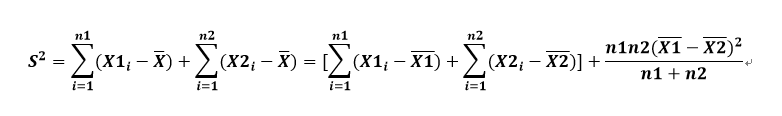
上式中右端第一项中括号内两个平方和反映了两个子序列内部的组内差异，称为组内偏差平方和，第二项反映了两组数据之间的组间差异，称为组间偏差平方和，要判断组间差异是否显著，就要考虑这两项的比值，我们用如下的F检验法进行显著性检验：

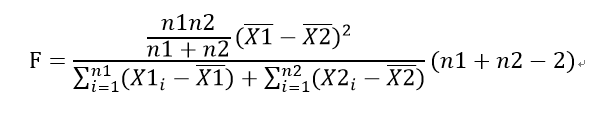
取置信水平为0.95，F的检验标准为：n=n1+n2≥50时，F值大于4；当10≤n＜50，F值大于5则通过检验，即认为两个子序列存在显著差异。通过对全部序列滑动计算每一年的F值，选取F值最大的年份并进行显著性检验，通过检验则该年作为转折年。为了避免子序列过短，滑动计算时只计算[5，n-5]区间的值。

均一性审查得到转折年后，需要进行均一性订正。订正使用方差分析法，其原理是根据方差的定义“表示变量取值相对于均值的偏离程度”，它反映出序列的离散程度，由于城市化改变了气象站周围的环境，使得最大风速的均值和方差均发生变化，因此使用方差分析法订正较为合适，其公式如下：

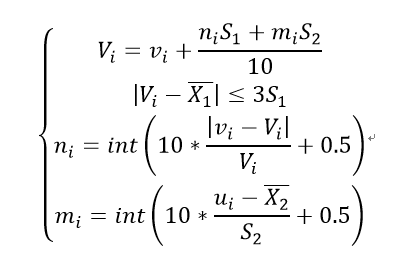
式中X1表示在城市化进程影响之前（即转折年之前）的最大风速序列的均值，S1表示其方差，ui为受到城市化影响之后（转折年之后，包括转折年）的最大风速序列减去后得到的序列，X2和S2分别为其均值和方差，Vi为将受到城市化影响的序列vi订正后的最大风速，int表示取整函数。

实现代码较长，可以扫下方二维码关注气海同途公众号，后台回复均一化。