随机性偏差模型（DFR）介绍

第一次翻译文章，可能有不少错误，但是希望可以对原文阅读起到帮助。

随机性偏差模型 (DFR) 是信息检索的最早模型之一，哈特的 2-泊松索引-模型 [1] 的最早模式之一。2-泊松模型基于在一系列的具有价值的文档所提供的词语，这些词语在相关文档中发生的概率比在不相关文档中发生的概率更高。

另一方面，有一些词语不包含于关键的文档，所以他们的频率遵循随机分布，是单一的泊松模型。哈特的模型中，首先作为检索模型由Robertson, Van Rijsbergen and Porter 探讨[4]。先后它由Robertson和Walker [3] 与标准概率模型结合，催生 了一系列BMs IR 模型 ，其中有知名的 BM25 这是霍加狓系统（Okapi system）的基础。
DFR 模型通过实例化框架的三个组成部分︰ 选择基本随机性模型、 应用第一次的正常化、 规范化词的频率。

基础随机模型(Basic Randomness Models)

DFR模型基于这样一个假设：“在相关文档中词频的频率在集合中更加发散，在文档d中词语t携带的信息更多”。换而言之，在包含随机模型M的文档中，d词语的重要程度与它出现的频率反相关。

公式（1）

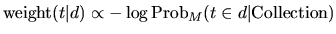
这里的下标 M 代表用来计算概率的随机性模型的类型。为了选择合适的模型 M 的随机性，我们可以使用不同的罐子模型（ urn models）。IR 被视为一个随机的过程，它使用随机从罐子里面取出图纸的模型或等价地随机放置彩球到罐子里面的模型。在这里我们使用文档代替罐子，使用词语代替彩球。每个词语，在该罐子一些多样性的发生是由于一些相关的词或短语被称为这个词的标记。现在有很多选择模型M的方法，这些都可以衍生基础的DFR模型。基础的模型由下表导出：

如果模型M是二项式分布，基础的模型记做p,并且计算的值如下：
公式（2）

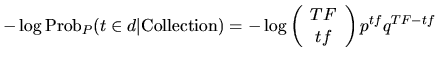
其中参数含义如下：

• TF 是词语 t 在集合中的频率
• tf 是词语 t 在文档 d 中的频率
• N 是集合中文档中的数量
• p=1/N 并且 q=1-p

相同的如果模型M是几何分布，基础模型记做G，并且计算的值如下：
公式（3）

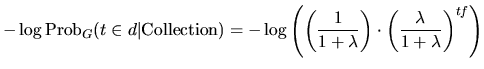
其中参数含义如下：

• λ=F/N

第一次的正常化(First Normalisation)

当文档中没有出现罕见的词，然后它是文档的信息的概率已经几乎为零的。相反地，如果一个罕见的术语在文档中有许多发生那么它必须是高概率 （几乎必然） 为文档所描述的主题。同样对 Ponte 和Croft的 [2] 的语言模型，我们在 DFR 模型中包括危险的因素。如果在文档中的词频高然而不包含文档信息的风险很小。在这种情况下公式 (1) 给出了很高的值，但风险降至最低也有提供小信息增益的负面影响。因此，而不是使用公式 (1) 所提供的全部重量，我们调整或光滑公式 (1) 的权重，通过考虑只有部分信息量是通过词语获得的︰
公式（4）

词语在有价值的集合（elite set）中出现的越多，词语更少依赖于随机性，因此更小的可能性 Prisk 为：
公式（5）

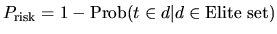
我们使用两种模型来计算信息的增益通过在文档中的词语：拉普拉斯L模型（ Laplace L model）和两种伯努力过程的比值 B（ratio of two Bernoulli’s processes B）。
公式（6）

其中参数含义：

• df 是指含有词语的文档数目
• TF 是词语 t 在集合中的频率
• tf 是词语 t 在文档 d 中的频率

词频率正常化（Term Frequency Normalisation）

在使用公式（4）前，文档的长度 dl 被规范到标准的长度 sl。因此，词频 tf 也被重新计算引入标准文档长度。
公式（7）

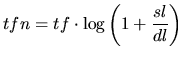
一个更加复杂的公式，如下：
公式（8）

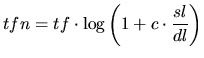
DFR 模型得出应用从生成的公式 (4)， 使用基本的 DFR 模型 （如公式 (2) 或 (3)） ，结合信息增益 （如公式 6) 模型和实现正常化词频率 （如公式 (7) 或公式 (8)）。

领域（fileds）

DFR 可以描述词语以各种不同的方式在不同领域发生的重要性︰

1. 每个字段的正常化︰词语在不同领域中出现的频率 通过在相应领域的代表字段长度统计实现正常化。这是表现为 PL2F 加权模型。可以使用通用的 PerFieldNormWeightingModel 模型生成其他每个字段正常化模型。
2. 多项式：来自不同领域的频率被参照在他们偏离预期的词语出现在这一领域的随机性。ML2 和 MDL2 模型执行此加权。

邻近（Proximity）

接近度可以通过 DFR 处理，通过考虑一对查询词语在预定义的大小窗口内出现次数。尤其是，DFRDependenceScoreModifier (DSM) 实现的 pBiL 和 pBiL2 的模型，测量相对于文档的长度的随机性，而不是对语料中的统计数据的随机性。

DFR模型和交叉熵

可以用交叉熵的概念对增益风险生成公式 (4) 进行不同的解读。香农在20 世纪 40 年代发表的通信的数学理论 [5] 确定最小平均码字长度是关于源词的概率值的熵。这一结果是在无声的编码定理（Noiseless Coding Theorem）的名义下被认知。无声一词是指在传输词的过程中不可能出现产生错误的假设。然而它可能导致来源不同的相同信息都可用。在一般情况下每个源产生不用的编码。在这种情况下，我们可以使用交叉熵来做两种来源比较的证据。当观测的两个对像返回相同的概率密度函数，并且在这种情况下交叉熵恰好与香农熵交叉熵减至最低。

我们拥有两个测试的随机性：第一个测试是 Prisk，和词语在有价值的文档中的分布有关，第二个是 ProbM，和文档在整个集合中的重要性有关。初次分配可以被视为新来源的的词语分布，并且在集合中词语的编码伴随着词语的分布可以被认为是初次的来源。两个概率分布的交叉熵的定义如下：
公式（9）

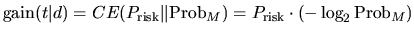
公式（9）是公式（4）在DFR模型中的实际联系。DFR模型可以等同地定义为两个概率测量的证据是两个不同的来源的随机性的量的发散。

想要知道更多有关于随机性框架的分布（Divergence from Randomness framework），你可以查到Gianni Amati或Amati和Van Rijsbergen的博士论文：Probabilistic models of information retrieval based on measuring divergence from randomness, TOIS 20(4):357-389, 2002.

[1] S.P. Harter. A probabilistic approach to automatic keyword indexing. PhD thesis, Graduate Library, The University of Chicago, Thesis No. T25146, 1974.
[2] J. Ponte and B. Croft. A Language Modeling Approach in Information Retrieval. In The 21st ACM SIGIR Conference on Research and Development in Information Retrieval (Melbourne, Australia, 1998), B. Croft, A.Moffat, and C.J. van Rijsbergen, Eds., pp.275-281.
[3] S.E. Robertson and S. Walker. Some simple approximations to the 2-Poisson Model for Probabilistic Weighted Retrieval. In Proceedings of the Seventeenth Annual International ACM-SIGIR Conference on Research and Development in Information Retrieval (Dublin, Ireland, June 1994), Springer-Verlag, pp. 232-241.
[4] S.E. Robertson, C.J. van Risjbergen and M. Porter. Probabilistic models of indexing and searching. In Information retrieval Research, S.E. Robertson, C.J. van Risjbergen and P. Williams, Eds. Butterworths, 1981, ch. 4, pp. 35-56.
[5] C. Shannon and W. Weaver. The Mathematical Theory of Communication. University of Illinois Press, Urbana, Illinois, 1949.
[6] B. He and I. Ounis. A study of parameter tuning for term frequency normalization, in Proceedings of the twelfth international conference on Information and knowledge management, New Orleans, LA, USA, 2003.
[7] B. He and I. Ounis. Term Frequency Normalisation Tuning for BM25 and DFR Model, in Proceedings of the 27th European Conference on Information Retrieval (ECIR’05), 2005.
[8] V. Plachouras and I. Ounis. Usefulness of Hyperlink Structure for Web Information Retrieval. In Proceedings of ACM SIGIR 2004.
[9] V. Plachouras, B. He and I. Ounis. University of Glasgow in TREC 2004: experiments in Web, Robust and Terabyte tracks with Terrier. In Proceedings of the 13th Text REtrieval Conference (TREC 2004), 2004.