[深度学习]Part2 集成学习Ch08-1——【DeepBlue学习笔记】

本文主要是介绍[深度学习]Part2 集成学习Ch08-1——【DeepBlue学习笔记】，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

本文仅供学习使用

集成学习Ch08-1

1. 集成学习(Ensemble Learning)
- 1.1 Bagging方法——过拟合（方差）
- - 1.1.1 训练过程
  - 1.1.2 预测过程
  - 1.1.3 代码实现
  - 1.1.4 subagging
- 1.2 随机森林(Random Forest)
- - 1.2.1 Extra Tree
  - 1.2.2 Totally Random Trees Embedding(TRTE)
  - 1.2.3 Isolation Forest(IForest)
  - 1.2.4 RF总结
  - 1.2.5 RF scikit-learn相关参数及代码实现
  - 1.2.6 随机森林的思考
- 1.3 Boosting——欠拟合（偏差）
- - 1.3.1 AdaBoost
  - - 1.3.1.1 算法原理
    - 1.3.1.2 扩展AdaBoost算法子模型权重系数求解
    - 1.3.1.3 算法构建过程
    - 1.3.1.4 直观理解
    - 1.3.1.5 AdaBoost scikit-learn相关参数
    - 1.3.1.6 总结
    - 1.3.1.7 代码实现
  - 1.3.2 梯度提升迭代决策树GBDT
  - - 1.3.2.1 直观理解
    - 1.3.2.2 算法原理
    - 1.3.2.3 回归算法和分类算法的区别
    - 1.3.2.4 总结
    - 1.3.2.5 GBDT scikit-learn相关参数
  - 1.3.3 Boosting算法总结
- 1.4 Bagging、Boosting的区别

1. 集成学习(Ensemble Learning)

集成学习(Ensemble Learning)的思想是将若干个学习器(分类器&回归器)组合之后产生一个新学习器——通过构建并结合多个学习期来完成学习任务，有时也被称为多分类系统(multi-classifier system)、基于委员会的学习(committee-based learning)等

集成算法的成功在于保证弱分类器的多样性(Diversity)。而且集成不稳定的算法也能够得到一个比较明显的性能提升。

集成学习的一般结构： 先产生一组个体学习器（individual learner），再用某种策略将它们结合起来。个体学习期通常由一个现有的学习算法从训练数据产生，此时集成中只包含同种类型的个体学习器——这样的集成是同质（homogeneous）的。同质集成中的个体学习器亦称基学习器（base learner），相应的学习算法称为基学习算法（base learning algorithm）；集成也可包含不同类型的个体学习器——这样的集成是异质的（heterogenous）。异质集成中的个体学习器由不同的学习算法生成，这时就不再有基学习算法。相应的，个体学习器常称为组件学习器（component learner）或直接称为个体学习器。
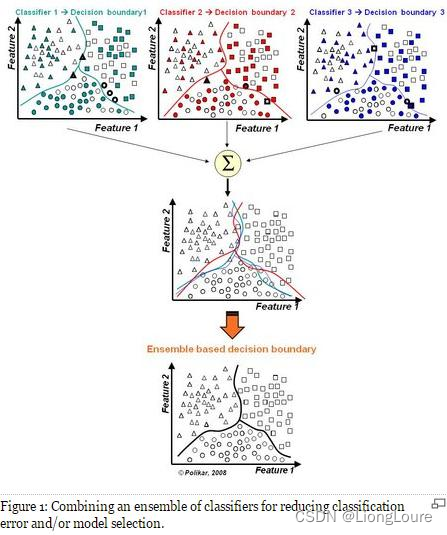
在这里插入图片描述

集成学习通过将多个学习器进行结合，常可获得比单一学习器显著优越的泛化性能。这对弱学习器（weak learner）尤为明显，因此集成学习的很多理论研究都是针对若学习器进行的，而基学习器有时也被直接称为弱学习器。弱分类器(weak learner)指那些分类准确率只稍微好于随机猜测的分类器(error rate < 0.5)，个体学习器至少不差于弱学习器；

在一般经验中，如果把好的和坏的东西掺到一起，那么通常结果会是比最坏的要好一些，比最好的要坏一些。集成学习把多个学习器结合起来，如何能获得比最好的单一学习器更好的性能呢？

集成学习的结果通过投票法（voting）产生，即“少数服从多数”，而要获得好的集成，个体学习器应“好而不同”，即个体学习器要有一定的准确性，即学习器不能太坏并且要有多样性（diversity），即学习器间有差异。
考虑二分类问题 $y\in \{-1,+1\}$ 和真实函数 $f$ ，假定基分类器的错误率为 $\varepsilon$ ，即对每个基分类器 ${{h}_{i}}$ 有： $P({{h}_{i}}(x)\ne f(x))=\varepsilon$ ，假设集成通过简单投票法结合 $T$ 个基分类器（假定T为奇数），若有超过半数的基分类器正确，则集成分类就正确： $F(x)=sign(\sum\limits_{i=1}^{T}{{{h}_{i}}(x)})$ ，若假设基分类器的错误率相互独立，则由Hoeffding不等式可知，集成的错误率为： $P(F(x)\ne f(x))=\sum\limits_{k=0}^{[T/2]}{\left( \begin{matrix} T \\ k \\\end{matrix} \right){{(1-\varepsilon )}^{\varepsilon }}{{\varepsilon }^{T-k}}}\le \exp (-\frac{1}{2}T{{(1-2\varepsilon )}^{2}})$
可见：随着集成中个体分类器数目 $T$ 的增大，集成的错误率将指数级下降，最终趋向于零。
数据很少和很多的时候，集成方法效果一样好——将数据都保留下来，并且通过某种方法将它们的结果合并起来（多数表决——合并后的分类器只有在一半以上的分类器出错时，才会得出最终的错误结果）
上述基于一个关键假设：基学习器的误差相互独立。在现实任务中，个体学习器是为解决同一个问题训练出来的，它们显然不可能相互独立！事实上，个体学习器的“准确性”和“多样性”本身就存在冲突。一般地，准确性很高之后，要增加多样性就需牺牲准确性。事实上，如何产生并结合“好而不同”的个体学习器，恰是集成学习研究的核心、
目前集成学习方法大致可分为两大类，即个体学习器间存在强依赖关系、必须串行生成的序列化方法，以及个体学习器见不存在强依赖关系、可同时生成的并行化方法；前者是Boosting，后者的代表是Bagging和随机森林（Random Forest）

常见的集成学习思想有：
• Bagging
• Boosting
• Stacking（见3）

Why need Ensemble Learning?

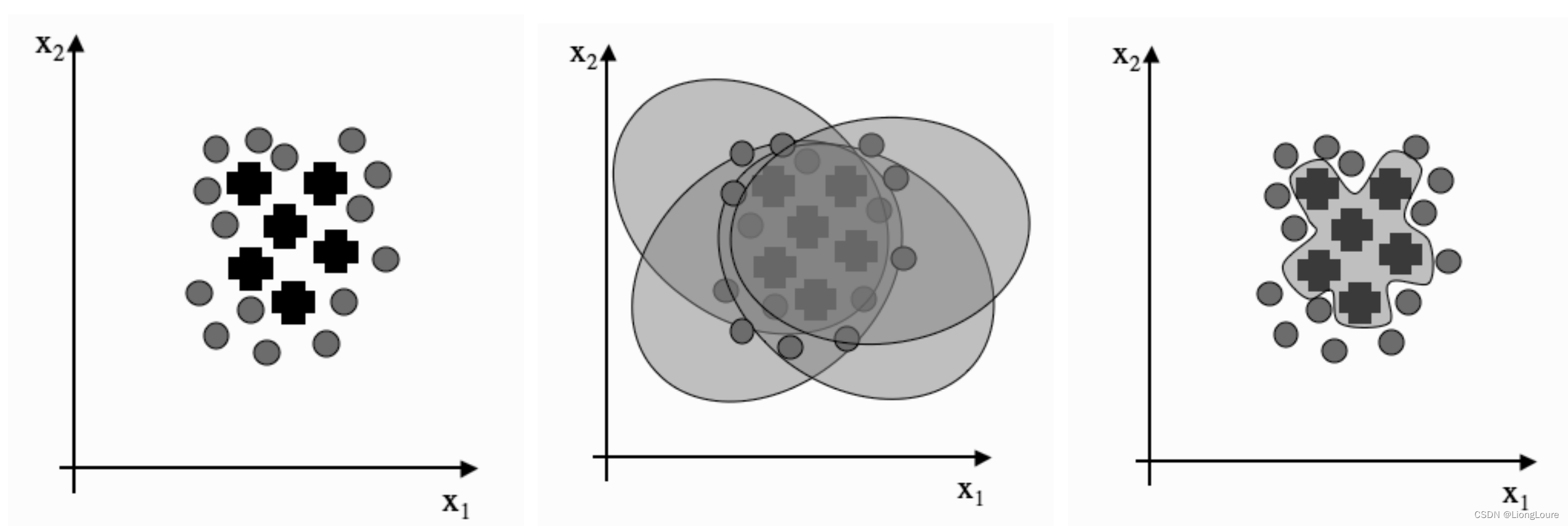
弱分类器间存在一定的差异性，这会导致分类的边界不同，也就是说可能存在错误。那么将多个弱分类器合并后，就可以得到更加合理的边界，减少整体的错误率，实现更好的效果；
对于数据集过大或者过小，可以分别进行划分和有放回的操作产生不同的数据子集，然后使用数据子集训练不同的分类器，最终再合并成为一个大的分类器；(一万条数据有放回的采样一万条子集，各子集不一定一样)
如果数据的划分边界过于复杂，使用线性模型很难描述情况，那么可以训练多个模型，然后再进行模型的融合；
对于多个异构的特征集的时候，很难进行融合，那么可以考虑每个数据集构建一个分类模型，然后将多个模型融合。

1.1 Bagging方法——过拟合（方差）

欲得到泛化性能强的集成，集成中的个体学习器应尽可能相互独立——设法使基学习器尽可能具有较大的差异：对训练样本进行采样，产生出若干个不同的子集，再从每个数据子集中训练出一个基学习器——如果采样出的每个子集都完全不同，显然无法确保产生比较好的基学习器——使用相互有交叠的采样子集。

bootstrap在计算机科学中要更加流行，因为计算机开机的时候也有一个bootstrap程序，那就是引导加载程序。英文中的bootstrap指靴带，来自短语“pull oneself up by one’s bootstrap”。18世纪德国文学家拉斯伯的小说《巴隆历险记》（Adventures of Baron Munchausen）中写：巴龙掉到湖里，在沉到湖底且异常绝望的时候，他用靴带把自己拉了上来。现意指不借助别人的力量，凭自己的努力获得成功。——bootstrap法是指用原样本自身的数据采样得出新的样本及统计量——自助法。

Bagging方法又叫做自举汇聚法(Bootstrap Aggregating)，思想是：在原始数据集上通过有放回的抽样的方式，重新选择出S个新数据集来分别训练S个分类器的集成技术。（确保数据多样性——模型多样性）是并行式集成学习方法最著名的代表，基于自助采样法（boostrap sampling）给定包含m个样本的数据集，随机取出一个样本放入采样集中，再把该样本放回初始数据集，采样出T个含m个训练样本的采样集，然后基于每个采样集训练出一个基学习器，再将这些基学习器进行结合，这就是Bagging的基本流程（Bootsrap AGGregatING的缩写）

Bagging方法（Brieiman，1996）训练出来的模型在预测新样本分类/回归的时候，会使用多数投票或者求均值的方式来统计最终的分类/回归结果。
Bagging方法的弱学习器可以是基本的算法模型，eg: Linear、Ridge、Lasso、 Logistic、Softmax、ID3、C4.5、CART、SVM、KNN等。

NOTE1： Bagging方式是有放回的抽样，并且每个子集的样本数量必须和原始样本数量一致，所以抽取出来的子集中是存在重复数据的，模型训练的时候允许存在重复数据。
NOTE2： 差不多有1/3的样本数据是不在Bagging的每个子模型的训练数据中的。（ $\underset{m\to \infty }{\mathop{\lim }}\,{{(1-\frac{1}{m})}^{m}}=\frac{1}{e}\approx 0.368$ ），可用作验证集来对泛化性能进行包外估计（out-of-bag estimate）

假定基学习器的计算复杂度为 $O (m)$ ，则Bagging的复杂度大致为 $T (O (m) + O (s))$ ，考虑到采样与投票/平均过程的复杂度 $O (s)$ ，而T通常是一个不太大的常数，因此，训练一个Bagging集成与直接使用基学习算法训练一个学习器的复杂度同阶——Bagging是一个高效的集成学习算法

1.1.1 训练过程

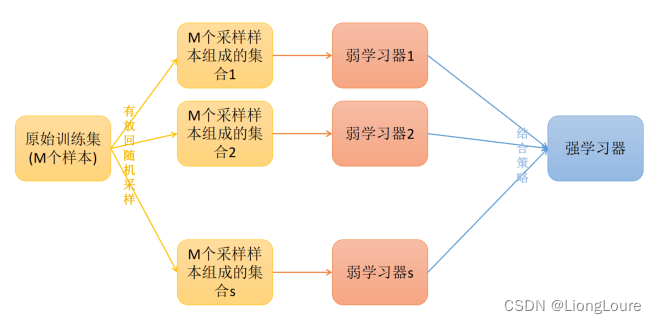
在这里插入图片描述
不妨令 ${{D}_{t}}$ 表示 ${{h}_{t}}$ 实际使用的训练样本集，令 ${{H}^{oob}}(x)$ 表示对样本x的包外预测，即仅考虑那些未使用x训练的基学习器在x上的预测，有： ${{H}^{oob}}(x)=\underset{y\in \gamma }{\mathop{\arg \max }}\,\sum\limits_{t=1}^{T}{\Iota ({{h}_{t}}(x)=y)\cdot \Iota (x\notin {{D}_{t}})}$ ，则Bagging泛化误差的包外估计为： ${{\varepsilon }^{oob}}=\frac{1}{|D|}\sum\limits_{(x,y)\in D}{\Iota ({{H}^{oob}}(x)\ne y)}$

事实上，包外样本还有许多其他用途：例如当基学习器是决策树时，可使用包外样本来辅助剪枝，或用于估计决策树中各节点的后验概率以辅助对零训练样本结点的处理；当基学习器是神经网络时，可使用包外样本来辅助早期停止以减少过拟合风险。

1.1.2 预测过程

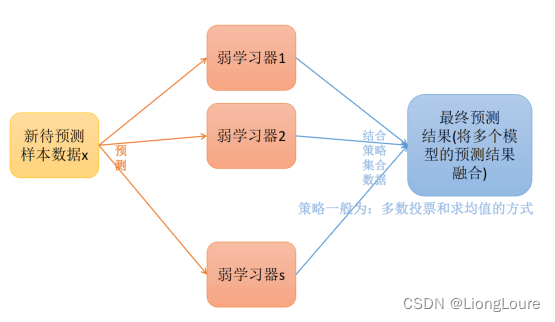
在这里插入图片描述
从偏差-方差分解的角度看，Bagging主要关注降低方差，因此它在不剪枝决策树、神经网络等易受样本扰动的学习器上效用更为明显。

1.1.3 代码实现

回归问题

import pandas as pd
import numpy as np
from sklearn.tree import DecisionTreeRegressor
from sklearn.metrics import r2_score'''
bagging 回归
'''
###数据
df = pd.DataFrame([[1, 10.56],[2, 27],[3, 39.1],[4, 40.4],[5, 58],[6, 60.5],[7, 79],[8, 87],[9, 90],[10, 95]],columns=['X', 'Y'])
# print(df)
M = []  ###用来存储弱学习器
n_trees = 100  ###构造的弱学习器的数量for i in range(n_trees):  ##循环训练我们的弱学习器###对样本进行有放回的抽样m次'''sample() 抽样n=None,  抽样数据的条数frac=None, 抽样的比例replace=False, 是否有放回抽样weights=None, 权重random_state=None, 随机数种子axis=None 维度'''tmp = df.sample(frac=1.0, replace=True)  ###不需要设置随机数种子# tmp = tmp.drop_duplicates()  # ##去重X = tmp.iloc[:, :-1]Y = tmp.iloc[:, -1]model = DecisionTreeRegressor(max_depth=1)model.fit(X, Y)M.append(model)###做预测
x = df.iloc[:, :-1]
y = df.iloc[:, -1]mode01 = DecisionTreeRegressor(max_depth=1)
mode01.fit(x, y)
y_hat_01 = mode01.predict(x)
print(y_hat_01)
print(mode01.score(x, y))
print("-" * 100)
res = np.zeros(df.shape[0])
for j in M:res += j.predict(x)
y_hat = res / n_trees
print(y_hat)
print('R2:', r2_score(y, y_hat))

分类问题

import numpy as np
import pandas as pd
from sklearn.tree import DecisionTreeClassifier
from sklearn.metrics import f1_score, accuracy_scoredf = pd.DataFrame([[0, 1], [1, 1], [2, 1], [3, -1], [4, -1],[5, -1], [6, 1], [7, 1], [8, 1], [9, -1]])
n_tree = 199
models = []for i in range(n_tree):df2 = df.sample(frac=1.0, replace=True)X = df2.iloc[:, :-1]Y = df2.iloc[:, -1]dec = DecisionTreeClassifier(max_depth=1)dec.fit(X, Y)models.append(dec)x = df.iloc[:, :-1]
y = df.iloc[:, -1]
total = np.zeros(df.shape[0])
for i in range(n_tree):total += np.array(models[i].predict(x))
print(total)
y_hat = np.sign(total)
print(y_hat)print(accuracy_score(y, y_hat))
print(f1_score(y, y_hat))
print("-" * 100)
model01 = DecisionTreeClassifier(max_depth=1)
model01.fit(x, y)
y_hat_01 = model01.predict(x)
print(y_hat_01)
print(accuracy_score(y, y_hat_01))
print(f1_score(y, y_hat_01))

1.1.4 subagging

subagging（子袋法，subsample+bagging）

1.2 随机森林(Random Forest)

随机森林分类器模型：from sklearn.ensemble import RandomForestClassifier
随机森林回归器模型：from sklearn.ensemble import RandomForestRegressor

随机森林（Breiman,2001） 是Bagging的一个扩展变体，在Bagging策略的基础上进行修改后的一种算法，RF在以决策树为基学习器构建Bagging集成的基础上，进一步在决策树的训练过程中引入了随机属性选择——传统决策树在选择划分属性时是在当前结点的属性集合（假定有d个属性）中选择一个最优属性；而在RF中，对基决策树的每个结点，先从该结点的属性集合中随机选择一个包含k个属性的子集，然后再从这个子集中选择一个最优属性用于划分。这里的参数k控制了随机性的引入程度：若令k=d，则基决策树的构建与传统决策树相同；若令k=1，则是随机选择一个属性用于划分；一般情况下，推荐值 $k={{\log }_{2}}d$

从原始样本集(n个样本)中用 Bootstrap采样(有放回重采样) 选出n个样本；
使用抽取出来的子数据集(存在重复数据)来训练决策树；从所有属性中随机选择K个属性，从K个属性中选择出最佳分割属性作为当前节点的划分属性，按照这种方式来迭代的创建决策树。
重复以上两步m次，即建立m棵决策树；
这m个决策树形成随机森林，通过投票表决结果决定数据属于那一类

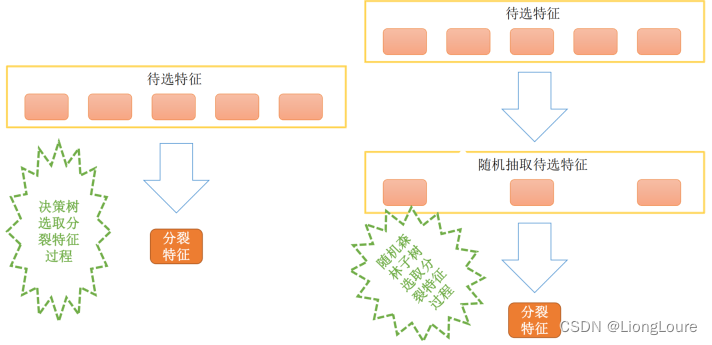
在这里插入图片描述

随机森林在很多显示任务中展现出强大的性能，被誉为“代表集成学习技术水平的方法”，与Bagging中基学习器的“多样性”仅通过样本扰动（通过对初始训练集采样）而来不同，随机森林中基学习器的多样性不仅来自样本扰动，还来自属性扰动，这就使得最终集成的泛化性性能可通过个体学习器之间差异度的增加而进一步提升。
随机森林的收敛性与Bagging相似，随机森林的起始性能往往相对较差，特别是在集成中只包含一个基学习器时——通过引入属性扰动，随机森林中个体学习器的性能往往有所降低——而随着个体学习器数目的增加，随机森林通常会收敛到更低的泛化误差
随机森林的训练效率常优于Bagging，因为在个体决策树的构建中，Bagging使用的是 “确定型”决策树，在选择划分属性时要对结点的所有属性进行考察，而随机森林使用的 “随机型”决策树则只需考察一个属性。

RF的推广算法

RF算法在实际应用中具有比较好的特性，应用也比较广泛，主要应用在：分类、回归、特征转换、异常点检测等。常见的RF变种算法如下：
• Extra Tree （有监督-分类、回归）
• Totally Random Trees Embedding(TRTE) ——特征转换
• Isolation Forest（异常点检测）

1.2.1 Extra Tree

Extra Tree是RF的一个变种，原理基本和RF一样，区别如下：

RF会随机重采样来作为子决策树的训练集，而Extra Tree每个子决策树采用原始数据集训练；
RF在选择划分特征点的时候会和传统决策树一样，会基于信息增益、信息增益率、基尼系数、均方差等原则来选择最优特征值；而Extra Tree会随机的选择一个特征值来划分决策树。

Extra Tree因为是随机选择特征值的划分点，这样会导致决策树的规模一般大于RF所生成的决策树。也就是说Extra Tree模型的方差相对于RF进一步减少。在某些情况下，Extra Tree的泛化能力比RF的强。

1.2.2 Totally Random Trees Embedding(TRTE)

TRTE是一种 非监督 的数据转化方式。将低维的数据集映射到高维，从而让映射到高维的数据更好的应用于分类回归模型。

TRTE算法的转换过程类似RF+KDTree算法的方法，建立T个决策树来拟合数据(是类似KD-Tree一样基于特征属性的方差选择划分特征)。当决策树构建完成后，数据集里的每个数据在T个决策树中叶子节点的位置就定下来了，将位置信息转换为向量就完成了特征转换操作

案例： 有3棵决策树，各个决策树的叶子节点数目分别为:5,5,4，某个数据x划分到第一个决策树的第3个叶子节点，第二个决策树的第一个叶子节点，第三个决策树的第四个叶子节点，那么最终的x映射特征编码为:(0,0,1,0,0, 1,0,0,0,0, 0,0,0,1)
在这里插入图片描述

1.2.3 Isolation Forest(IForest)

IForest是一种异常点检测算法，使用类似RF的方式来检测异常点（离群点）；IForest算法和RF算法的区别在于：

在随机采样的过程中，一般只需要少量数据即可；
在进行决策树构建过程中，IForest算法会随机选择一个划分特征，并对划分特征随机选择一个划分阈值；
IForest算法构建的决策树一般深度max_depth是比较大的。

区别原因：目的是异常点检测，所以只要能够区分异常的即可，不需要大量数据；

对于异常点的判断，则是将测试样本x拟合到m棵决策树上。计算在每棵树上该样本的叶子节点的深度ht(x)。从而计算出平均深度h(x)；然后就可以使用下列公式计算样本点x的异常概率值，p(x,m)的取值范围为[0,1]，越接近于1，则是异常点的概率越大。

备注：如果落在的叶子节点为正常样本点，那么当前决策树不考虑，如果所有决策树上都是正常样本点，那么直接认为异常点概率为0.

$p(x,m)={{2}^{-\frac{h(x)}{c(m)}}},c(m)=2\ln (m-1)+\xi -2\frac{m-1}{m}$ ，其中m为样本个数， $\xi$ 为欧拉常数

1.2.4 RF总结

决策树有一个常见的问题，即倾向于紧密地拟合训练数据（过拟合）。在随机森林中，许多决策树同时被训练，但是每棵树只接收一个自举的（bootstrapped）样本（即有放回的随机采样，抽样次数与原始样本树相同），并且每个结点在确定最佳分裂时只会考虑全部特征的一个子集。这个由随机树组成的森林（随机森林因此而得名）通过投票决定样本的预测分类。

RF的主要优点：

训练可以并行化(每棵树的构建过程相互独立)，对于大规模样本的训练具有速度的优势，并具有接近线性的加速；
由于进行随机选择决策树划分特征列表，这样在样本维度比较高的时候，仍然具有比较高的训练性能；
给以给出各个特征的重要性列表；
由于存在随机抽样（分布均匀），训练出来的模型方差小，泛化能力强，能够缓解过拟合的情况；
RF实现简单；
对于部分特征的缺失不敏感。

RF的主要缺点：

在某些噪音比较大的特征上（数据特别异常情况），RF模型容易陷入过拟合；
取值比较多的划分特征对RF的决策会产生更大的影响，从而有可能影响模型的效果。

1.2.5 RF scikit-learn相关参数及代码实现

随机森林分类器模型：from sklearn.ensemble import RandomForestClassifier
创建随机森林分类器对象：randomforest = RandomForestClassifier(random_state=0,n_jobs=-1)
使用熵创建随机森林的分类器对象：randomforest_entropy = RandomForestClassifier(criterion='entropy',random_state=0)
训练模型：model = randomforest.fit(features,target)

max_features： 决定每个结点需要考虑的特征的最大数量，允许输入的变量类别包括整型（特征的数量）、浮点型（特征的百分比）和 sqrt（特征数量的平方根），默认值为auto（相当于sqrt）。
n_estimators: 设置森林中包含决策树的数量；
n_jobs = -1: 来指定使用所有可用的CPU核进行训练，并且该参数不仅仅对随机森林分类器有效。

随机森林回归模型：from sklearn.ensemble import RandomForestRegressor
创建随机森林回归对象：randomforest = RandomForestRegressor(random_state=0,n_jobs=-1)
训练模型：model = randomforest.fit(features,target)

每棵树使用一个自举的样本子集，并且在每个节点决策规则仅考虑一部分特征：

max_features： 决定每个结点需要考虑的特征的最大数量，默认值为特征总数的平方根。
bootstrap: 设置是否使用有放回的抽样，默认值为True；
n_estimators: 设置森林中包含决策树的数量，默认值为10；

在这里插入图片描述

import pandas as pd
import numpy as np
import sys
# from sklearn.preprocessing import Imputer
from sklearn.impute import SimpleImputer
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler, MinMaxScaler  ##标准化，归一化
from sklearn.decomposition import PCA
from sklearn.model_selection import GridSearchCVpd.set_option("display.max_columns", None)##读取数据
datas = pd.read_csv('F:/datas/risk_factors_cervical_cancer.csv', sep=',')
# print(datas.head())
# print(datas.info())
names = datas.columns
# print(names)
# sys.exit()
###数据清洗
datas.replace('?', np.nan, inplace=True)
# print(datas.info())
# sys.exit()
# print(datas.head())
###使用Imputer进行缺省值的填充 列填充
# imputer = Imputer(missing_values='NaN', strategy='mean', axis=0)
imputer = SimpleImputer()
datas = imputer.fit_transform(datas)
datas = pd.DataFrame(datas, columns=names)
# print(datas.head())
# print(datas.info())###获取特征属性X 和目标属性Y
X = datas.iloc[:, :-4]
Y = datas.iloc[:, -4:].astype('int')
# print(X.info())
# print(Y.info())###数据分割
x_train, x_test, y_train, y_test = train_test_split(X, Y, test_size=0.2, random_state=10)###构建一个管道
###数据标准化，数据归一化 （数据量纲） 决策树来说我们其实不需要做这个操作
##标准化：把数据转化为均值为0，方差为1的
##归一化：把数据压缩到0-1###PCA降维
models = [Pipeline([('standarscaler', StandardScaler()),('pca', PCA()),('RF', RandomForestClassifier())]),Pipeline([('pca', PCA(n_components=0.5)),('RF', RandomForestClassifier(n_estimators=50, max_depth=1))])]
'''
###设置参数
params = {'pca__n_components':[0.5,0.6,0.7,0.8,0.9],'RF__n_estimators':[50,100,150],'RF__max_depth':[1,3,5,7]}
##网格调参
model = GridSearchCV(estimator=models[0],param_grid=params,cv=5)
##训练
model.fit(x_train,y_train)
print('最优参数：',model.best_params_)
print('最优模型：',model.best_estimator_)
print('最优模型的分数：',model.best_score_)
'''model = models[1]
model.fit(x_train, y_train)
print(model.score(x_train, y_train))
print(model.score(x_test, y_test))# ###保存模型
# from sklearn.externals import joblib
# joblib.dump(model,'./model/risk01.m')

可视化随机森林——比较（和可视化）每个特征的相对重要性——不纯度（比如分类器中的基尼不纯度或熵，以及回归模型中的方差）的平均减少量较大的分裂特征时更重要的特征。

想要知道随机森林中最重要的特征——计算并可视化每个特征的重要性（Feature importance）
随机森林分类器模型：from sklearn.ensemble import RandomForestClassifier
可视化模型：import matplotlib.pyplot as plt
numpy：import numpy as np
创建随机森林分类器对象：randomforest = RandomForestClassifier(random_state=0,n_jobs=-1)
训练模型：model = randomforest.fit(features,target)
计算特征重要性：importance = model.feature_improtances_
查看特征的重要程度：model.feature_improtances_
将特征的重要性按降序排列：indices = np.argsort(importances)[::-1]
按照特征的重要性对特征名称重新排序：names = [iris.feature_names[i] for i in indices]
创建图：plt.figure()
创建图表题：plt.title('Feature Importance')
添加数据条：plt.bar(range(features.shape[1]), importances[indices])
将特征名称添加为x轴标签：plt.xticks(range(features.shape[1]), names, rotation=90)
显示图：plt.show()

关于特征的重要性有两点需要注意：——值越大，说明该特征越重要（所有特征的重要性分数相加等于1）

scikit-learn需要将nominal型分类特征分解为多个二元特征，使得特征的重要性分散到各个二元特征中。这样的话，即使原来的分类特征非常重要，分解后的特征往往也就没那么重要了；
如果两个特征高度相关，并且其中一个有很高的重要性，就会使另一个特征的重要性显得稍低，如果不考虑这种情况，模型的效果会受到影响

选择随机森林中的重要特征构建模型：

随机森林分类器模型：from sklearn.ensemble import RandomForestClassifier
特征矩阵模型：from sklearn.feature_selection import SelectFromModel
创建随机森林分类器对象：randomforest = RandomForestClassifier(random_state=0,n_jobs=-1)
创建对象，选择重要性大于或等于阈值的特征：selector = SelectFromModel(randomforest, threshold=0.3)
使用选择器创建新的特征矩阵：features_important = selector.fit_transform(features, target)
使用重要的特征训练随机森林模型：model = randomforest.fit(features_important, target)

首先使用所有特征训练一个随机森林模型，并使用训练得到的模型来确定重要的特征。有两点需要注意：

经过 one-hot编码的nominal型分类特征的重要性被稀释到二元特征中；
一对高度相关的特征，其重要性被集中在其中一个特征上，而不是均匀分布在这两个特征上。

处理不均衡分类——class_weight=‘balanced’:

创建随机森林分类器对象：randomforest = RandomForestClassifier(random_state=0,n_jobs=-1,class_weight='balanced')

使用袋外误差（Out-of-Bag Error）评估随机森林模型——在不使用交叉验证的情况下评估随机森林模型：

随机森林分类器模型：from sklearn.ensemble import RandomForestClassifier
创建随机森林分类器对象：randomforest = RandomForestClassifier(random_state=0,obb_score=True,n_jobs=-1')
训练模型：model = randomforest.fit(features,target)
查看袋外误差：randomforest.obb_score_

在随机森林中，每个决策树使用自举的样本子集进行训练。这意味着对于每棵树而言，都有未参与训练的样本子集。这些样本被称为袋外（Out-of-Bag，OOB）样本。袋外样本可以用作测试集来评估随机森林的性能。
对于每个样本，算法将其真实值与未使用该样本进行训练的树模型子集产生的预测值进行比较。计算所有样本的总得分，就能得到一个随机森林的性能指标。OOB分数评估法可以作为交叉验证的替代方案。

1.2.6 随机森林的思考

在随机森林的构建过程中，由于各棵树之间是没有关系的，相对独立的；在构建的过程中，构建第m棵子树的时候，不会考虑前面的m-1棵树。

思考：
如果在构建第m棵子树的时候，考虑到前m-1棵子树的结果，会不会对最终结果产生有益的影响？（Boosting）
各个决策树组成随机森林后，在形成最终结果的时候能不能给定一种既定的决策顺序呢？(也就是那颗子树先进行决策、那颗子树后进行决策)

1.3 Boosting——欠拟合（偏差）

Boosting是一族可将若学习器提为强学习器的算法。提升学习（Boosting）是一种机器学习技术，可以用于回归和分类的问题，它每一步产生弱预测模型(如决策树)，并加权累加到总模型中；如果每一步的弱预测模型的生成都是依据损失函数的梯度方式的，那么就称为梯度提升(Gradient boosting)；

工作机制： 先从初始训练集训练出一个基学习器，再根据基学习器的表现对训练样本分布进行调整，使得先前基学习器做错的训练样本在后续受到更多关注，然后基于调整后的样本分布来训练下一个基学习器；如此反复进行，直至基学习器数目达到事先指定的值T，最终将这T个基学习器进行加权拟合。

提升技术的意义： 如果一个问题存在弱预测模型，那么可以通过提升技术的办法得到一个强预测模型；

常见的模型有：
• Adaboost
• Gradient Boosting(GBT/GBDT/GBRT)——（GBDT—XGB/Light GBM）
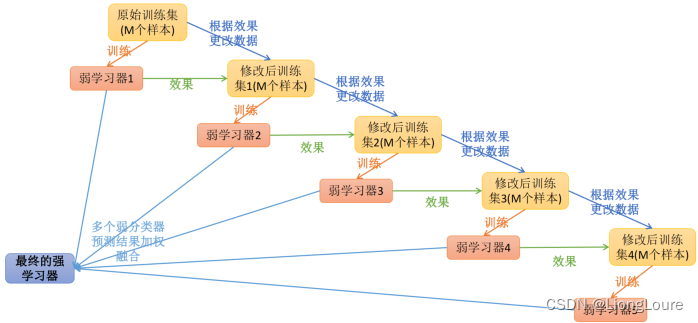
在这里插入图片描述
在原算法中，训练集被划分为三块，第一个分类器在第一和第三块数据上训练，在第二和第三块数据测试。所有在测试中被错分的数据，以及随机选取的等量的正确分类的数据，一起重新组成一个新的数据集点。第二个分类器在这个新的训练集进行训练，然后这两个分类器都在最后一个数据集上测试。对于某个数据点，如果它们产生了相同的输出结果，那么这个数据点就被忽略，否则就将其加进另一个新数据集。

1.3.1 AdaBoost

from sklearn.ensemble import AdaBoostClassifier

1.3.1.1 算法原理

Adaptive Boosting（AdaBoost-Freund and Schapire.1997）是一种迭代算法。每轮迭代中会在训练集上产生一个新的学习器，然后使用该学习器对所有训练样本进行预测，以评估每个样本的重要性(Informative)。换句话来讲就是，算法/子模型会为每个样本赋予一个权重，每次用训练好的学习器标注/预测各个样本(训练数据)，如果某个样本点被预测的越正确，则将样本权重降低；否则提高样本的权重。权重越高的样本在下一个迭代训练中所占的权重就越大，也就是说越难区分的样本在训练过程中会变得越重要；（初始值为1/N）

整个迭代过程直到错误率足够小或者达到一定的迭代次数为止——样本权重w、学习器权重a——噪声点（异常数据）的影响较大
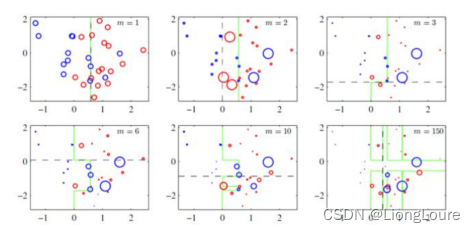
在这里插入图片描述
Adaboost算法将基分类器的线性组合作为强分类器，同时给分类误差率较小的基本分类器以大的权值，给分类误差率较大的基分类器以小的权重值——基于加性模型（additive model）；构建的线性组合为：

$f(x)=\sum\limits_{m=1}^{M}{{{\alpha }_{m}}{{G}_{m}}(x)}$

最终分类器是在线性组合的基础上进行Sign函数转换：

$G(x)=sign(f(x))=sign[\sum\limits_{m=1}^{M}{{{\alpha }_{m}}{{G}_{m}}(x)}]$

Sign函数:
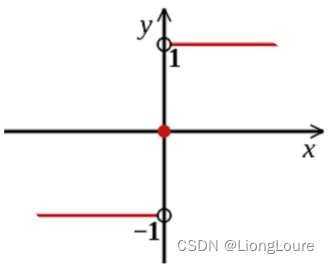
在这里插入图片描述

AdaBoost算法原理:

最终的强学习器： $G(x)=sign(f(x))=sign[\sum\limits_{m=1}^{M}{{{\alpha }_{m}}{{G}_{m}}(x)}]$

损/失函数(以错误率作为损失函数)： $\sum\limits_{i=1}^{n}{{{w}_{i}}=1};\text{ }loss=\sum\limits_{i=1}^{n}{{{w}_{i}}I(G({{x}_{i}})\ne {{y}_{i}})}$ （视为0-1损失）

损失函数(上界)： $loss=\sum\limits_{i=1}^{n}{{{w}_{i}}I(G({{x}_{i}})\ne {{y}_{i}})}\text{ }\le \sum\limits_{i=1}^{n}{{{w}_{i}}{{e}^{-{{y}_{i}}f(x)}}}$

第k-1轮的强学习器： ${{f}_{k-1}}(x)=\sum\limits_{j=1}^{k-1}{{{\alpha }_{j}}{{G}_{j}}(x)}$

第k轮的强学习器： ${{f}_{k}}(x)=\sum\limits_{j=1}^{k}{{{\alpha }_{j}}{{G}_{j}}(x)}$ ， ${{f}_{k}}(x)={{f}_{k-1}}(x)+{{\alpha }_{k}}{{G}_{k}}(x)$

损失函数： $loss({{\alpha }_{m}},{{G}_{m}}(x))=\sum\limits_{i=1}^{n}{{{w}_{1,i}}{{e}^{-{{y}_{i}}({{f}_{m-1}}(x)+{{\alpha }_{m}}{{G}_{m}}(x))}}}\text{ }$

$loss({{\alpha }_{m}},{{G}_{m}}(x))=\sum\limits_{i=1}^{n}{{{w}_{1,i}}{{e}^{-{{y}_{i}}{{f}_{m-1}}(x)}}{{e}^{-{{y}_{i}}{{\alpha }_{m}}{{G}_{m}}(x)}}}\overset{{{{\bar{w}}}_{mi}}={{w}_{1,i}}{{e}^{-{{y}_{i}}{{f}_{m-1}}(x)}}}{\mathop{\to }}\,\text{ =}\sum\limits_{i=1}^{n}{{{{\bar{w}}}_{mi}}{{e}^{-{{y}_{i}}{{\alpha }_{m}}{{G}_{m}}(x)}}}$

使下列公式达到最小值的αm和Gm就是AdaBoost算法的最终解
$loss({{\alpha }_{m}},{{G}_{m}}(x))=\sum\limits_{i=1}^{n}{{{{\bar{w}}}_{mi}}{{e}^{-{{y}_{i}}{{\alpha }_{m}}{{G}_{m}}(x)}}}$

G这个分类器在训练的过程中，是为了让误差率最小，所以可以认为G越好其实就是误差率越小。
${{G}_{m}}*(x)=\underset{{{G}_{m}}(x)}{\mathop{\min }}\,\sum\limits_{i=1}^{n}{{{{\bar{w}}}_{mi}}I}(G({{x}_{i}})\ne {{y}_{i}})$
${{\varepsilon }_{m}}=P({{G}_{m}}(x)\ne y)=\sum\limits_{i=1}^{n}{{{{\bar{w}}}_{mi}}I}(G({{x}_{i}})\ne {{y}_{i}})=\sum\limits_{G({{x}_{i}})\ne {{y}_{i}}}^{{}}{{{{\bar{w}}}_{mi}}}$

机器学习-周志华书中的推导过程

基学习器的线性组合： $H(x)=\sum\limits_{t=1}^{T}{{{\alpha }_{t}}{{h}_{t}}(x)}$
最小化指数损失函数（exponential loss function）: ${{\ell }_{\exp }}(H|D)={{\mathbb{R}}_{x\sim D}}[{{e}^{-f(x)H(x)}}]$
若 $H (x)$ 能令指数损失函数最小化： $\frac{\partial {{\ell }_{\exp }}(H|D)}{\partial H(x)}=-{{e}^{-H(x)}}P(f(x)=1|x)+{{e}^{H(x)}}P(f(x)=-1|x)=0\Rightarrow H(x)=\frac{1}{2}\ln \frac{P(f(x)=1|x)}{P(f(x)=-1|x)}$
因此，有： $sign(H(x))=sign(\frac{1}{2}\ln \frac{P(f(x)=1|x)}{P(f(x)=-1|x)})=\left\{ \begin{matrix} 1,P(f(x)=1|x)>P(f(x)=-1|x) \\ -1,P(f(x)=1|x)<P(f(x)=-1|x) \\ \end{matrix} \right.=\underset{y\in \{-1,1\}}{\mathop{\arg \max }}\,P(f(x)=y|x)$
这意味这 $s i g n (H (x))$ 达到了贝叶斯最优错误率。换言之，若指数损失函数最小化，则分类错误率也将最小化；这说明指数损失函数时分类任务原本0/1损失函数的一致的（consistent）替代损失函数。
在AdaBoost算法中，第一个基分类器 ${{h}_{1}}$ 是通过直接将基学习算法用于初始数据分布而得；此后迭代地生成 ${{h}_{t}}$ 和 ${{\alpha }_{t}}$ ，当基分类器 ${{h}_{t}}$ 基于分布 ${{D}_{t}}$ 产生后，该基分类器的权重 ${{\alpha }_{t}}$ 应使得 ${{\alpha }_{t}{h}_{t}}$ 最小化指数损失函数：
${{\ell }_{\exp }}({{\alpha }_{t}}{{h}_{t}}|{{D}_{t}})={{\mathbb{E}}_{x\sim D}}[{{e}^{-f(x){{\alpha }_{t}}{{h}_{t}}(x)}}]={{\mathbb{E}}_{x\sim D}}[{{e}^{-{{\alpha }_{t}}}}\mathbb{I}(f(x)={{h}_{t}}(x))+{{e}^{{{\alpha }_{t}}}}\mathbb{I}(f(x)\ne {{h}_{t}}(x))]={{e}^{-{{\alpha }_{t}}}}{{P}_{x\sim D}}(f(x)={{h}_{t}}(x))+{{e}^{{{\alpha }_{t}}}}{{P}_{x\sim D}}(f(x)\ne {{h}_{t}}(x))={{e}^{-{{\alpha }_{t}}}}(1-{{\varepsilon }_{t}})+{{e}^{{{\alpha }_{t}}}}{{\varepsilon }_{t}}$
其中： ${{\varepsilon }_{t}}={{P}_{x\sim D}}(f(x)\ne {{h}_{t}}(x))$ ，考虑指数损失函数的导数： $\frac{\partial {{\ell }_{\exp }}({{\alpha }_{t}}{{h}_{t}}|{{D}_{t}})}{\partial {{\alpha }_{t}}(x)}={{e}^{-{{\alpha }_{t}}}}(1-{{\varepsilon }_{t}})+{{e}^{{{\alpha }_{t}}}}{{\varepsilon }_{t}}=0$ ，解得： ${{\alpha }_{t}}=\frac{1}{2}\ln (\frac{1-{{\varepsilon }_{t}}}{{{\varepsilon }_{t}}})$ ——权重更新公式
AdaBoost算法在获得 ${{H}_{t-1}}$ 之后样本分布将进行调整，使下一轮基学习器 ${{h}_{t}}$ 能纠正 ${{H}_{t-1}}$ 的全部错误，即最小化： ${{\ell }_{\exp }}({{H}_{t-1}}+{{h}_{t}}|D)$ ，简化为： ${{\ell }_{\exp }}({{H}_{t-1}}+{{h}_{t}}|D)={{\mathbb{E}}_{x\sim D}}[{{e}^{-f(x)({{H}_{t-1}}(x)+{{h}_{t}}(x))}}]={{\mathbb{E}}_{x\sim D}}[{{e}^{-f(x){{H}_{t-1}}(x)}}{{e}^{-f(x){{h}_{t}}(x)}}]$ 。
注意到， ${{f}^{2}}(x)={{h}_{t}}^{2}(x)=1$ ，对上式进行泰勒展开，可得： ${{\ell }_{\exp }}({{H}_{t-1}}+{{h}_{t}}|D)\simeq {{\mathbb{E}}_{x\sim D}}[{{e}^{-f(x){{H}_{t-1}}(x)}}(1-f(x){{h}_{t}}(x)+\frac{{{f}^{2}}(x){{h}_{t}}^{2}(x)}{2})]={{\mathbb{E}}_{x\sim D}}[{{e}^{-f(x){{H}_{t-1}}(x)}}(1-f(x){{h}_{t}}(x)+\frac{1}{2})]$
于是，理想的基学习器： ${{h}_{t}}(x)=\underset{h}{\mathop{\arg \min }}\,{{\ell }_{\exp }}({{H}_{t-1}}+h|D)=\underset{h}{\mathop{\arg \min }}\,{{\mathbb{E}}_{x\sim D}}[{{e}^{-f(x){{H}_{t-1}}(x)}}(1-f(x)h(x)+\frac{1}{2})]=\underset{h}{\mathop{\arg \min }}\,{{\mathbb{E}}_{x\sim D}}[{{e}^{-f(x){{H}_{t-1}}(x)}}f(x)h(x)]=\underset{h}{\mathop{\arg \min }}\,{{\mathbb{E}}_{x\sim D}}[\frac{{{e}^{-f(x){{H}_{t-1}}(x)}}}{{{\mathbb{E}}_{x\sim D}}[{{e}^{-f(x){{H}_{t-1}}(x)}}]}f(x)h(x)]$
注意到： ${{\mathbb{E}}_{x\sim D}}[{{e}^{-f(x){{H}_{t-1}}(x)}}]$ 是一个常数，令 ${{D}_{t}}$ 表示一个分布： ${{D}_{t}}(x)=\frac{D(x){{e}^{-f(x){{H}_{t-1}}(x)}}}{{{\mathbb{E}}_{x\sim D}}[{{e}^{-f(x){{H}_{t-1}}(x)}}]}$ ，则根据数学期望的定义，这等价于： ${{h}_{t}}(x)=\underset{h}{\mathop{\arg \min }}\,{{\mathbb{E}}_{x\sim D}}[\frac{{{e}^{-f(x){{H}_{t-1}}(x)}}}{{{\mathbb{E}}_{x\sim D}}[{{e}^{-f(x){{H}_{t-1}}(x)}}]}f(x)h(x)]=\underset{h}{\mathop{\arg \min }}\,{{\mathbb{E}}_{x\sim{{D}_{t}}}}[f(x)h(x)]$
由 $f(x),h(x)\in \{-1,+1\}$ ，有： $f(x)h(x)=1-2\mathbb{I}(f(x)\ne h(x))$
则理想的基学习器： ${{h}_{t}}(x)=\underset{h}{\mathop{\arg \min }}\,{{\mathbb{E}}_{x\sim{{D}_{t}}}}[\mathbb{I}(f(x)\ne h(x))]$
由此可见，理想的 ${{h}_{t}}$ 将分布 ${{D}_{t}}$ 下最小化分类误差。因此，弱分类器将基于分布 ${{D}_{t}}$ 来训练，且针对 ${{D}_{t}}$ 的分类误差小于0.5。这在一定程度上类似“残差逼近”的思想，考虑到 ${{D}_{t}}$ 和 ${{D}_{t+1}}$ 的关系，有：
${{D}_{t+1}}(x)=\frac{D(x){{e}^{-f(x){{H}_{t}}(x)}}}{{{\mathbb{E}}_{x\sim D}}[{{e}^{-f(x){{H}_{t}}(x)}}]}=\frac{D(x){{e}^{-f(x){{H}_{t-1}}(x)}}{{e}^{-f(x){{\alpha }_{t}}{{h}_{t}}(x)}}}{{{\mathbb{E}}_{x\sim D}}[{{e}^{-f(x){{H}_{t}}(x)}}]}=D(x)\cdot {{e}^{-f(x){{\alpha }_{t}}{{h}_{t}}(x)}}\frac{{{\mathbb{E}}_{x\sim D}}[{{e}^{-f(x){{H}_{t-1}}(x)}}]}{{{\mathbb{E}}_{x\sim D}}[{{e}^{-f(x){{H}_{t}}(x)}}]}$ ——更新公式
从基于加性模型迭代式优化指数损失函数的角度推导出上述算法。

1.3.1.2 扩展AdaBoost算法子模型权重系数求解

$loss({{\alpha }_{m}},{{G}_{m}}(x))=\sum\limits_{i=1}^{n}{{{{\bar{w}}}_{mi}}{{e}^{-{{y}_{i}}{{\alpha }_{m}}{{G}_{m}}(x)}}}=\sum\limits_{G({{x}_{i}})={{y}_{i}}}^{{}}{{{{\bar{w}}}_{mi}}{{e}^{-{{\alpha }_{m}}}}}+\sum\limits_{G({{x}_{i}})\ne {{y}_{i}}}^{{}}{{{{\bar{w}}}_{mi}}{{e}^{{{\alpha }_{m}}}}}$

$=\sum\limits_{G({{x}_{i}})={{y}_{i}}}^{{}}{{{{\bar{w}}}_{mi}}{{e}^{-{{\alpha }_{m}}}}}+{{\varepsilon }_{m}}{{e}^{{{\alpha }_{m}}}}=\sum\limits_{G({{x}_{i}})={{y}_{i}}}^{{}}{{{{\bar{w}}}_{mi}}{{e}^{-{{\alpha }_{m}}}}}+{{\varepsilon }_{m}}{{e}^{{{\alpha }_{m}}}}+\sum\limits_{G({{x}_{i}})\ne {{y}_{i}}}^{{}}{{{{\bar{w}}}_{mi}}{{e}^{-{{\alpha }_{m}}}}}-\sum\limits_{G({{x}_{i}})\ne {{y}_{i}}}^{{}}{{{{\bar{w}}}_{mi}}{{e}^{-{{\alpha }_{m}}}}}$

$=\sum\limits_{i=1}^{n}{{{{\bar{w}}}_{mi}}{{e}^{-{{\alpha }_{m}}}}}+{{\varepsilon }_{m}}{{e}^{{{\alpha }_{m}}}}-{{\varepsilon }_{m}}{{e}^{-{{\alpha }_{m}}}}={{e}^{-{{\alpha }_{m}}}}+{{\varepsilon }_{m}}{{e}^{{{\alpha }_{m}}}}-{{\varepsilon }_{m}}{{e}^{-{{\alpha }_{m}}}}$

$loss({{\alpha }_{m}},{{G}_{m}}(x))={{e}^{-{{\alpha }_{m}}}}+{{\varepsilon }_{m}}{{e}^{{{\alpha }_{m}}}}-{{\varepsilon }_{m}}{{e}^{-{{\alpha }_{m}}}}$ ， $\frac{\partial loss}{\partial {{\alpha }_{m}}}=-{{e}^{-{{\alpha }_{m}}}}+{{\varepsilon }_{m}}{{e}^{{{\alpha }_{m}}}}+{{\varepsilon }_{m}}{{e}^{-{{\alpha }_{m}}}}$

$\Rightarrow \frac{\partial loss}{\partial {{\alpha }_{m}}}=0\Rightarrow -{{e}^{-{{\alpha }_{m}}}}+{{\varepsilon }_{m}}{{e}^{{{\alpha }_{m}}}}+{{\varepsilon }_{m}}{{e}^{-{{\alpha }_{m}}}}=0\Rightarrow ({{\varepsilon }_{m}}-1){{e}^{-{{\alpha }_{m}}}}+{{\varepsilon }_{m}}{{e}^{{{\alpha }_{m}}}}=0$

$\Rightarrow {{\varepsilon }_{m}}{{e}^{{{\alpha }_{m}}}}=(1-{{\varepsilon }_{m}}){{e}^{-{{\alpha }_{m}}}}\Rightarrow \frac{{{e}^{{{\alpha }_{m}}}}}{{{e}^{-{{\alpha }_{m}}}}}=\frac{(1-{{\varepsilon }_{m}})}{{{\varepsilon }_{m}}}\Rightarrow {{e}^{2{{\alpha }_{m}}}}=\frac{(1-{{\varepsilon }_{m}})}{{{\varepsilon }_{m}}}$

$\Rightarrow \ln {{e}^{2{{\alpha }_{m}}}}=\ln \frac{(1-{{\varepsilon }_{m}})}{{{\varepsilon }_{m}}}\Rightarrow 2{{\alpha }_{m}}=\ln \frac{(1-{{\varepsilon }_{m}})}{{{\varepsilon }_{m}}}\Rightarrow {{\alpha }_{m}}=\frac{1}{2}\ln \frac{(1-{{\varepsilon }_{m}})}{{{\varepsilon }_{m}}}$

1.3.1.3 算法构建过程

假设训练数据集T：
$T=\{({{X}_{1}},{{Y}_{1}}),({{X}_{2}},{{Y}_{2}}),...,({{X}_{n}},{{Y}_{n}})\}$
初始化训练数据权重分布：
${{D}_{1}}=({{w}_{11}},{{w}_{12}},...{{w}_{1i}},...,{{w}_{1n}}),{{w}_{1i}}=\frac{1}{n},i=1,2,..,n$
使用具有权值分布Dm的训练数据集学习，得到基本分类器
${{G}_{m}}(x):x\to \{-1,+1\}$
计算Gm(x)在训练集上的分类误差
${{\varepsilon }_{m}}=P({{G}_{m}}(x)\ne y)=\sum\limits_{i=1}^{n}{{{{\bar{w}}}_{mi}}I}(G({{x}_{i}})\ne {{y}_{i}})=\sum\limits_{G({{x}_{i}})\ne {{y}_{i}}}^{{}}{{{{\bar{w}}}_{mi}}}$
计算Gm(x)模型的权重系数 ${{\alpha }_{m}}$ ：
${{\alpha }_{m}}=\frac{1}{2}\ln \frac{(1-{{\varepsilon }_{m}})}{{{\varepsilon }_{m}}}$
权重训练数据集的权值分布
${{D}_{m+1}}=({{w}_{m+1,1}},{{w}_{m+1,2}},...{{w}_{m+1,i}},...,{{w}_{m+1,n}}),{{w}_{m+1,i}}=\frac{{{w}_{m,i}}}{{{Z}_{m}}}{{e}^{-{{\alpha }_{m}}{{y}_{i}}{{G}_{m}}(x)}}$
这里Zm是规范化因子(归一化)
${{Z}_{m}}=\sum\limits_{i=1}^{n}{{{w}_{m,i}}{{e}^{-{{y}_{i}}{{\alpha }_{m}}{{G}_{m}}({{x}_{i}})}}}$
构建基本分类器的线性组合
$f(x)=\sum\limits_{m=1}^{M}{{{\alpha }_{m}}{{G}_{m}}(x)}$
得到最终分类器
$[G(x)=sign(f(x))=sign(\sum\limits_{m=1}^{M}{{{\alpha }_{m}}{{G}_{m}}(x)})$

1.3.1.4 直观理解

使用下列样本作为训练数据，试图使用AdaBoost算法学习一个强分类器：

初始化训练数据集的权值分布：
${{D}_{1}}=({{w}_{11}},{{w}_{12}},...,{{w}_{1i}},...{{w}_{1n}}),{{w}_{1i}}=\frac{1}{N},i=1,2,...,N$
可得： ${{w}_{1i}}=0.1$
对于m=1，在权值分布为D1的训练数据上，阈值v取2.5时误差率最低，故基本分类器为：
${{G}_{1}}(x)=\left\{ \begin{matrix} 1,x<2.5 \\ -1,x>2.5 \\ \end{matrix} \right.$
G1(x)在训练数据集上的误差率： ${{\varepsilon }_{1}}=P({{G}_{1}}({{x}_{i}})\ne {{y}_{i}})=0.3$
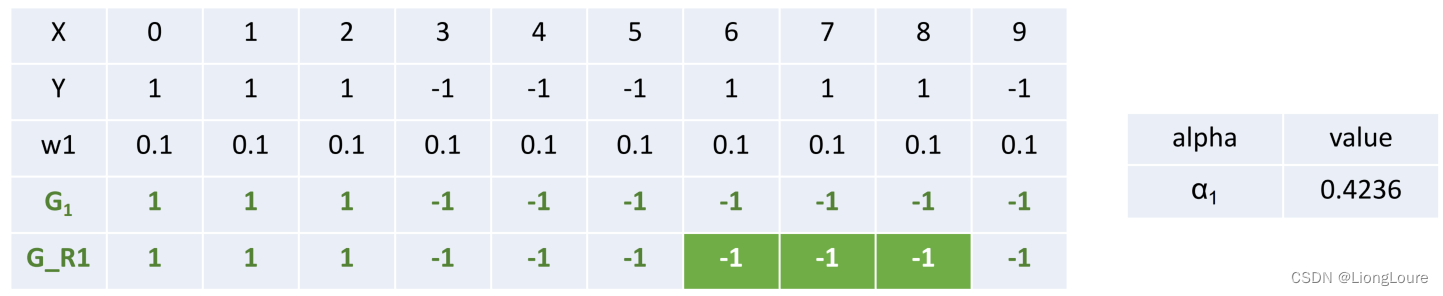
计算G1的系数： ${{\alpha }_{1}}=\frac{1}{2}\ln \frac{1-{{\varepsilon }_{1}}}{{{\varepsilon }_{1}}}=0.4236$
更新数据集的权值分布：
${{D}_{m+1}}=({{w}_{m+1,1}},{{w}_{m+1,2}},...{{w}_{m+1,i}},...,{{w}_{m+1,n}}),{{w}_{m+1,i}}=\frac{{{w}_{m,i}}}{{{Z}_{m}}}{{e}^{-{{\alpha }_{m}}{{y}_{i}}{{G}_{m}}(x)}}$
${{D}_{2}}=({{w}_{21}},{{w}_{22}},...,{{w}_{2n}})=(0.0714,0.0714,0.0714,0.0714,0.0714,0.0714,0.1667,0.1667,0.1667,0.0714)$
${{f}_{1}}(x)=0.4236{{G}_{1}}(x)$
分类器sign(f1(x))在训练数据集上有3个误分类点
对于m=2

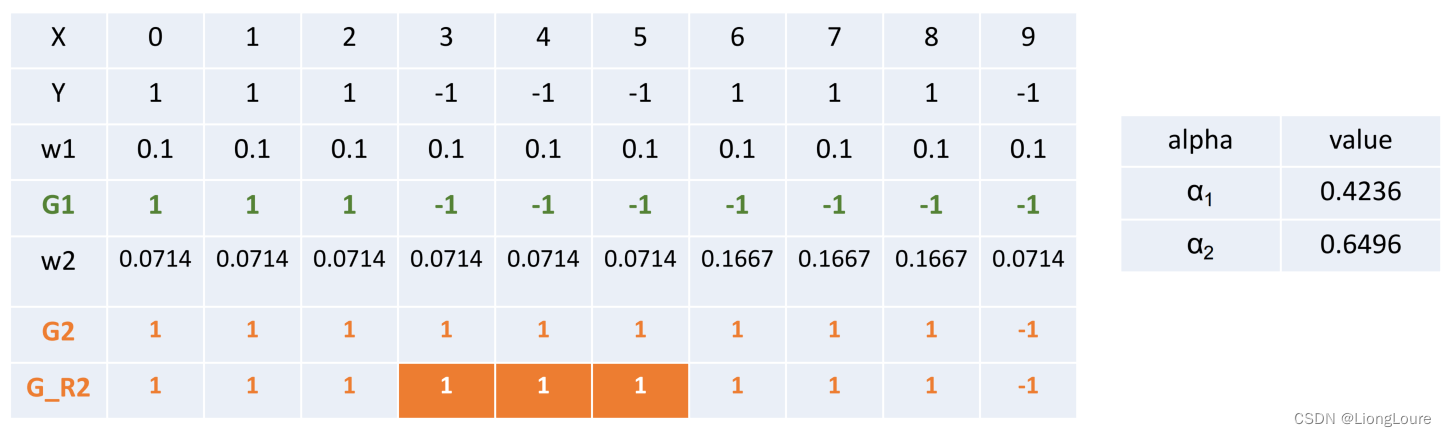
在权值分布为D2的训练数据上，阈值v取8.5时误差率最低，故基本分类器为：
${{G}_{2}}(x)=\left\{ \begin{matrix} 1,x<8.5 \\ -1,x>8.5 \\ \end{matrix} \right.$
G2(x)在训练数据集上的误差率： ${{\varepsilon }_{2}}=P({{G}_{2}}({{x}_{i}})\ne {{y}_{i}})=0.0714\times 3=0.2142$
计算G2的系数： ${{\alpha }_{2}}=\frac{1}{2}\ln \frac{1-{{\varepsilon }_{2}}}{{{\varepsilon }_{2}}}=0.6496$
更新数据集的权值分布：

${{f}_{2}}(x)=0.4236{{G}_{1}}(x)+0.6496{{G}_{2}}(x)$
分类器sign(f2(x))在训练数据集上有3个误分类点
对于m=3

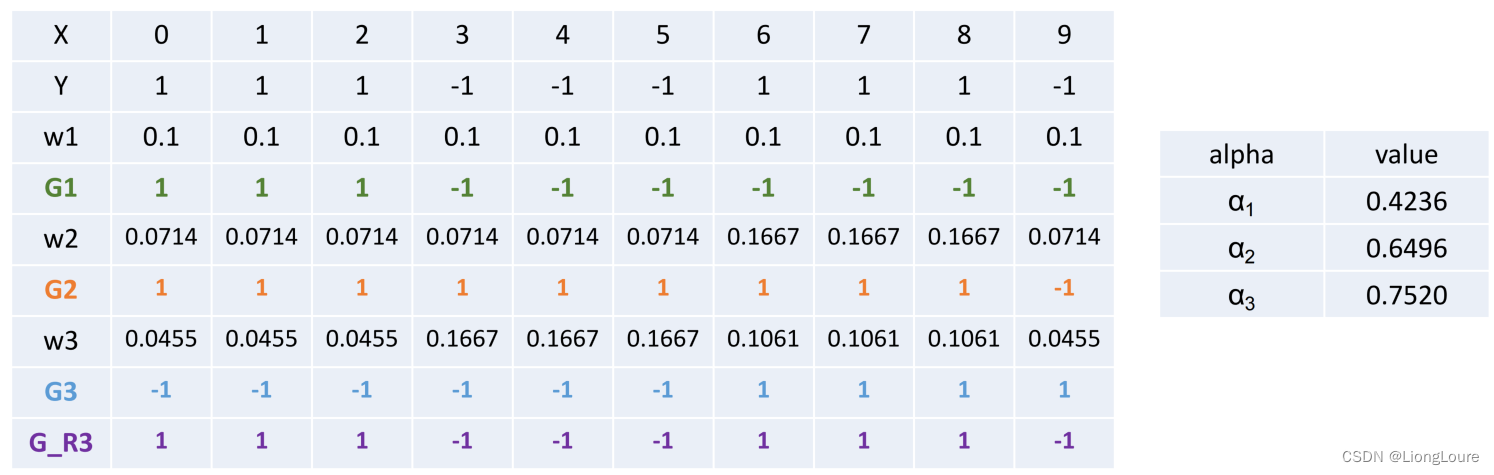
在权值分布为D3的训练数据上，阈值v取5.5时误差率最低，故基本分类器为：
${{G}_{3}}(x)=\left\{ \begin{matrix} 1,x<5.5 \\ -1,x>5.5 \\ \end{matrix} \right.$
G3(x)在训练数据集上的误差率： ${{\varepsilon }_{2}}=P({{G}_{2}}({{x}_{i}})\ne {{y}_{i}})=0.0455\times 3=0.182$
计算G3的系数： ${{\alpha }_{3}}=\frac{1}{2}\ln \frac{1-{{\varepsilon }_{3}}}{{{\varepsilon }_{3}}}=0.7520$
更新数据集的权值分布：

${{f}_{3}}(x)=0.4236{{G}_{1}}(x)+0.6496{{G}_{2}}(x)+0.7520{{G}_{3}}(x)$
分类器sign(f3(x))在训练数据集上有0个误分类点

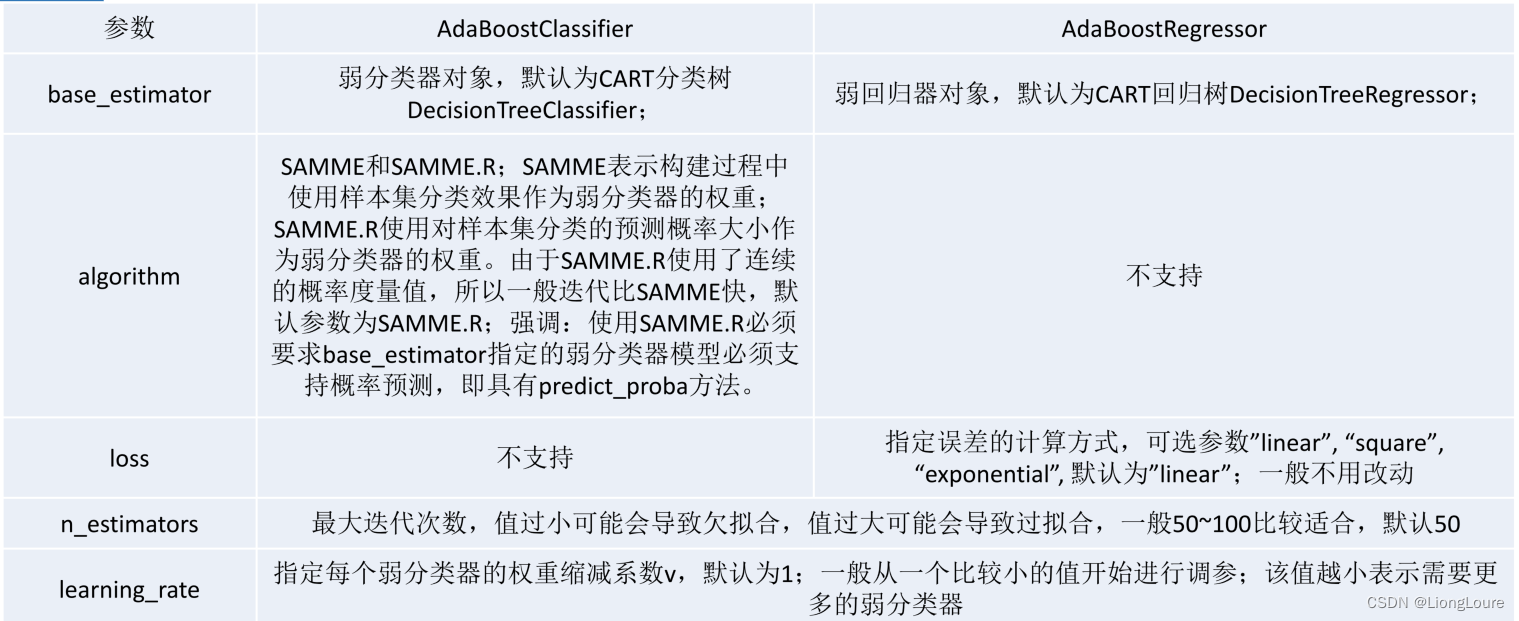
1.3.1.5 AdaBoost scikit-learn相关参数

在这里插入图片描述
$f(x)=\sum\limits_{m=1}^{M}{{{\alpha }_{m}}{{G}_{m}}(x)}\overset{添加缩减系数v}{\mathop{\to }}\,f(x)=\sum\limits_{m=1}^{M}{v{{\alpha }_{m}}{{G}_{m}}(x)}$

1.3.1.6 总结

AdaBoost的优点如下：
• 可以处理连续值和离散值；
• 模型的鲁棒性比较强；
• 解释强，结构简单。

AdaBoost的缺点如下：
• 对异常样本敏感，异常样本可能会在迭代过程中获得较高的权重值，最终影响模型效果。

1.3.1.7 代码实现

import sysimport numpy as np
import pandas as pd
from sklearn.tree import DecisionTreeClassifier
from sklearn.metrics import f1_score, accuracy_scoredf = pd.DataFrame([[0, 1],[1, 1],[2, 1],[3, -1],[4, -1],[5, -1],[6, 1],[7, 1],[8, 1],[9, -1]])X = df.iloc[:, :-1]
Y = df.iloc[:, -1]###第一个弱学习器
## 初始化样本权重
w1 = np.ones(df.shape[0]) / df.shape[0]
# print(w1)
# sys.exit()
##构造弱分类器G1
model1 = DecisionTreeClassifier(max_depth=1)
model1.fit(X, Y, sample_weight=w1)
###误差率
# print(w1[model1.predict(X)!=Y])
e1 = sum(w1[model1.predict(X) != Y])
# print(e1)
###弱学习器G1的权重α1
a1 = 0.5 * np.log((1 - e1) / e1)
# print(a1)
# sys.exit()
###第二个弱学习器G2
###更新样本权重值
w2 = w1 * np.exp(-a1 * Y * model1.predict(X))
# print(w2)
w2 = np.array(w2 / sum(w2))  ##归一化
# print(w2)
# sys.exit()
##训练模型G2
model2 = DecisionTreeClassifier(max_depth=1)
model2.fit(X, Y, sample_weight=w2)###误差率e2
e2 = sum(w2[model2.predict(X) != Y])
print(e2)
###求G2的权重α2
a2 = 0.5 * np.log((1 - e2) / e2)
print(a2)
# f = a1*G1+a2*G2
# sys.exit()###第三个弱学习器 G3
###更新样本权重值
w3 = w2 * np.exp(-a2 * Y * model2.predict(X))
# print(w3)
w3 = np.array(w3 / sum(w3))  ##归一化
print(w3)
###训练模型G3
model3 = DecisionTreeClassifier(max_depth=1)
model3.fit(X, Y, sample_weight=w3)###误差率e3
e3 = sum(w3[model3.predict(X) != Y])
# print(e3)
###求G3的权重α3
a3 = 0.5 * np.log((1 - e3) / e3)
# print(a3)
# f = a1*G1+a2*G2+a3*G3##最终分类器的线性组合f3
# f3 =a1*model1+a2*model2+a3*model3
## 最终的分类器G
# G = sign(f3)
##预测
y_hat = np.sign(a1 * model1.predict(X) + a2 * model2.predict(X) + a3 * model3.predict(X))
print(Y.tolist())
print(y_hat)

from sklearn.ensemble import AdaBoostClassifier
创建adaboost树分类器对象：adaboost = AdaBoostClassifier(random_state=0)
训练模型：model = adaboost.fit(features, target)

我们可以使用AdaBoostClassifier或AdaBoostRegressor实现AdaBoost：

base_estimator： 表示训练弱模型的学习算法。这个参数几乎不需要改变，因为到目前为止决策树（默认值）是AdaBoost最常用的学习算法；
n_estimators： 是需要迭代训练的模型数量；
learning_rate： 是每个若模型的权重变化率，默认值为1。减小这个参数值意味着权重变化的幅度变小，这会使模型的训练速度变慢（但有时会使模型的性能更好）。
loss： 是AdaBoostRegressor独有的参数，它设置了在更新权重时所用的损失函数。其默认值为线性损失函数，但是可以改为平方（square）或者指数函数（exponential）

1.3.2 梯度提升迭代决策树GBDT

GBDT也是Boosting算法的一种，但是和AdaBoost算法不同；区别如下： AdaBoost算法是利用前一轮的弱学习器的误差来更新样本权重值，然后一轮一轮的迭代；GBDT也是迭代，但是GBDT要求弱学习器必须是回归CART模型，而且 GBDT在模型训练的时候，是要求模型预测的样本损失尽可能的小。——拟合负梯度

备注：所有GBDT算法中，底层都是回归树。

别名：GBT(Gradient Boosting Tree)、GTB(Gradient Tree Boosting)、 GBRT(Gradient Boosting Regression Tree)、GBDT(Gradient Boosting Decison Tree)、MART(Multiple Additive Regression Tree)

$\begin{matrix} {{f}_{t-1}}(x) \\ L(y,{{f}_{t-1}}(x)) \\ \end{matrix}\overset{训练弱学习器:{{h}_{t}}(x)}{\mathop{\to }}\,\begin{matrix} {{f}_{t}}(x) \\ L(y,{{f}_{t-1}}(x)+{{h}_{t}}(x)) \\ \end{matrix}$

1.3.2.1 直观理解

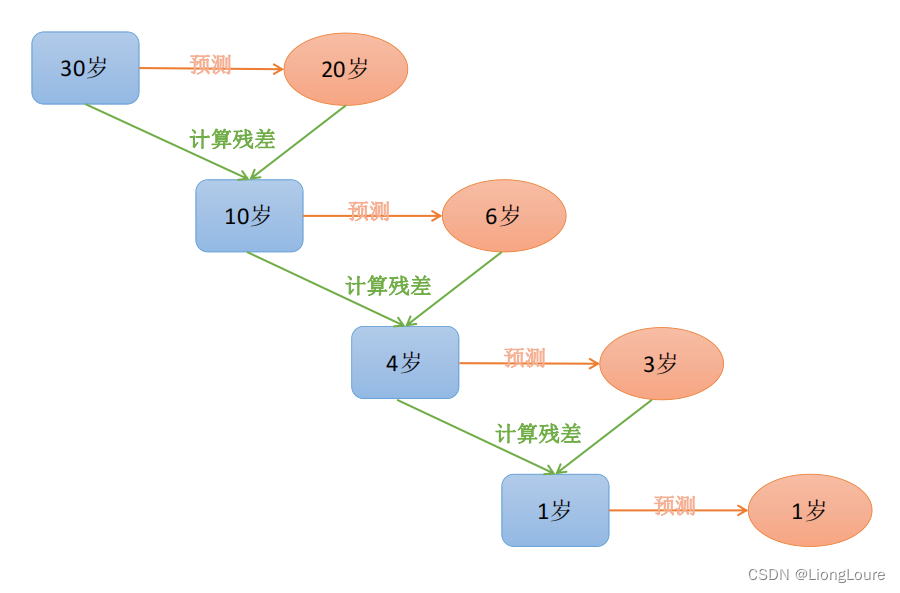
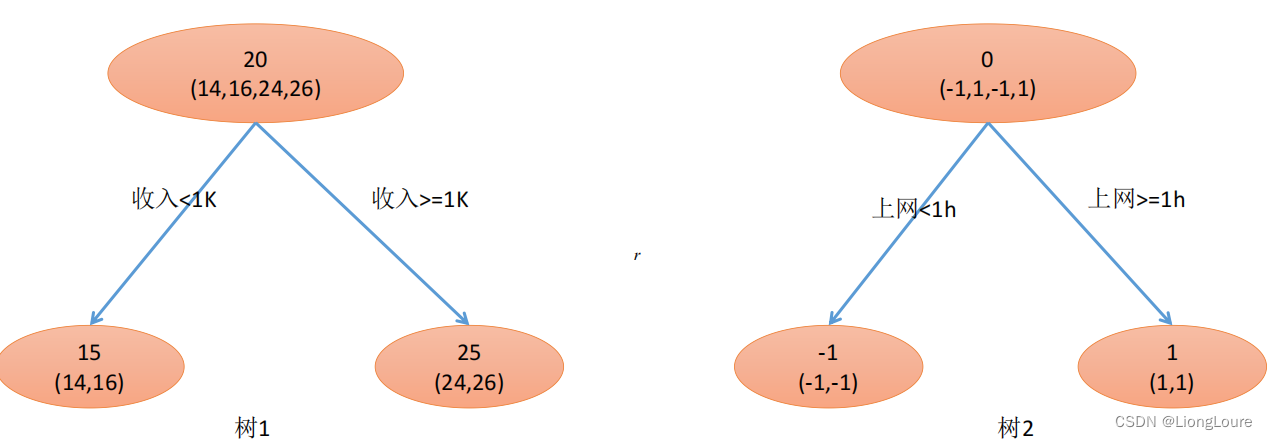
在这里插入图片描述

当给定步长时候，给定一个步长step，在构建下一棵树的时候使用 step*残差值 作为输入值，这种方式可以减少过拟合的发生

GBDT由三部分构成：DT(Regression Decistion Tree)、GB(Gradient Boosting)和Shrinkage(衰减)
由多棵决策树组成，所有树的结果累加起来就是最终结果

迭代决策树和随机森林的区别：
• 随机森林使用抽取不同的样本构建不同的子树，也就是说第 m 棵树的构建和前 m-1 棵树的结果是没有关系的
• 迭代决策树在构建子树的时候，使用之前子树构建结果后形成的残差作为输入数据构建下一个子树；然后最终预测的时候按照子树构建的顺序进行预测，并将预测结果相加

1.3.2.2 算法原理

给定输入向量X和输出变量Y组成的若干训练样本(X1,Y1),(X2,Y2)…(Xn,Yn)，目标是找到近似函数F(X)，使得损失函数L(Y,F(X))的损失值最小。

损失函数一般采用最小二乘损失函数或者绝对值损失函数： $L(y,F(x))=\frac{1}{2}{{(y-F(x))}^{2}},L(y,F(x))=|y-F(x)|$

最优解为： $F*(x)=\underset{F}{\mathop{\arg \min }}\,L(y,F(x))$

假定F(X)是一族最优基函数fi(X)的加权和：
$F(x)=\sum\limits_{i=0}^{M}{{{f}_{i}}(x)}\overset{防止每个学习器能力过强，可能导致过拟合；给定一个缩放系数v}{\mathop{\to }}\,F(x)=v\sum\limits_{i=0}^{M}{{{f}_{i}}(x)}$

以贪心算法的思想扩展得到Fm(X)，求解最优f：
${{F}_{m}}(x)={{F}_{m-1}}(x)+\underset{f}{\mathop{\arg \min }}\,\sum\limits_{i=1}^{n}{L({{y}_{i}},{{F}_{m-1}}({{x}_{i}})+{{f}_{m}}({{x}_{i}}))}$

以贪心法在每次选择最优基函数f时仍然困难，使用梯度下降的方法近似计算给定常数函数F0(X)：
${{F}_{0}}(x)=\underset{c}{\mathop{\arg \min }}\,\sum\limits_{i=1}^{n}{L({{y}_{i}},c)}$

计算损失函数的负梯度值：
${{y}_{im}}=-{{[\frac{\partial L({{y}_{i}},F({{x}_{i}}))}{\partial F({{x}_{i}})}]}_{F(x)={{F}_{m-1}}(x)}}$

使用数据 ${{x}_{i}},{{y}_{im}})$ (i=1……n )计算拟合残差找到一个CART回归树，得到第m棵树：
${{c}_{mj}}=\underset{c}{\mathop{\arg \min }}\,\sum\limits_{{{x}_{i}}\in lea{{f}_{j}}}^{{}}{L({{y}_{im}},c)},{{f}_{m}}(x)=\sum\limits_{j=1}^{|leaf{{|}_{m}}}{{{c}_{mj}}I}(x\in lea{{f}_{mj}})$

更新模型：
${{F}_{m}}(x)={{F}_{m-1}}(x)+\sum\limits_{j=1}^{|leaf{{|}_{m}}}{{{c}_{mj}}I}(x\in lea{{f}_{mj}})\Rightarrow F(x)={{F}_{0}}(x)+\sum\limits_{m=1}^{M}{\sum\limits_{j=1}^{|leaf{{|}_{m}}}{{{c}_{mj}}I}(x\in lea{{f}_{mj}})}$

1.3.2.3 回归算法和分类算法的区别

两者唯一的区别就是选择不同的损失函数、以及对应的负梯度值和模型初值采用不一样的值。

回归算法选择的损失函数一般是均方差(最小二乘)和绝对值误差，分类算法中一般选择对数损失函数来表示。

${{\alpha }_{im}}=-{{[\frac{\partial L({{y}_{i}},F({{x}_{i}}))}{\partial F({{x}_{i}})}]}_{F(x)={{F}_{m-1}}(x)}}$

均方差损失函数：
损失函数： $L(y,{{F}_{m}}(x))=\frac{1}{2}{{(y-{{F}_{m}}(x))}^{2}}$
负梯度值： ${{y}_{im}}={{y}_{i}}-{{F}_{m-1}}(x)$
初始值：一般采用均值作为初始值。

绝对误差损失函数：
损失函数： $L(y,{{F}_{m}}(x))=|y-{{F}_{m}}(x)|$
负梯度值： ${{y}_{im}}=sign({{y}_{i}}-{{F}_{m-1}}(x))$
初始值：一般采用中值作为初始值。

对数损失函数(二分类)：
损失函数： $L(y,{{F}_{m}}(x))=-(y\ln ({{p}_{m}})+(1-y)\ln (1-{{p}_{m}})),{{p}_{m}}=\frac{1}{1+{{e}^{-{{F}_{m}}(x)}}}$
负梯度值： ${{y}_{im}}={{y}_{i}}-{{p}_{m}}$
初始值：一般采用ln(正样本个数/负样本个数)作为初始值。

对数损失函数(多分类K)：
损失函数： $L(y,{{F}_{ml}}(x))=-\sum\limits_{k=1}^{K}{{{y}_{k}}\ln {{p}_{k}}(x)},{{p}_{k}}(x)=\frac{\exp {{f}_{k}}(x)}{\sum\limits_{l=1}^{K}{\exp {{f}_{l}}(x)}}$
负梯度值： ${{y}_{iml}}={{y}_{il}}-{{p}_{ml}}(x)$
初始值：一般采用0作为初始值。

1.3.2.4 总结

GBDT的优点如下：
• 可以处理连续值和离散值；
• 在相对少的调参情况下，模型的预测效果也会不错；
• 模型的鲁棒性比较强。

GBDT的缺点如下：
• 由于弱学习器之间存在关联关系，难以并行训练模型。也就是模型训练的速度慢

1.3.2.5 GBDT scikit-learn相关参数

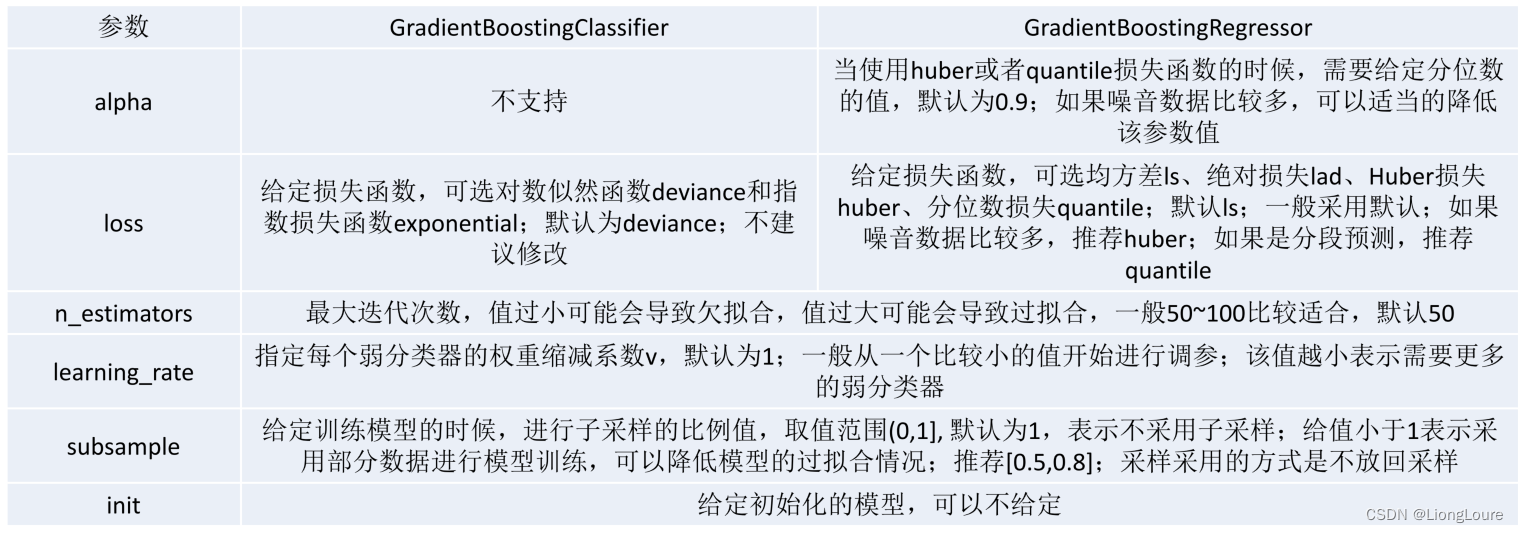
在这里插入图片描述

import pandas as pd
import numpy as np
from sklearn.tree import DecisionTreeRegressor
from sklearn.metrics import r2_score
from sklearn.model_selection import train_test_split###数据
df = pd.DataFrame([[1, 5.56], [2, 5.7], [3, 5.91], [4, 6.4], [5, 6.8], [6, 7.05], [7, 8.9], [8, 8.7], [9, 9], [10, 9.05]],columns=['X', 'Y'])
# df = pd.read_csv('./datas/boston_housing.data', sep='\s+', header=None)
X = df.iloc[:, :-1]
Y = df.iloc[:, -1]
y = Y  ##保留原始的Y###Fm = F0+v*f1+v*f2+v*f3+...v*fm###F0
F0 = np.mean(Y)
M = [F0]
##f1第一棵树 标签（label） Y-F0
Y = Y - F0 ##残差作为梯度，回归（平方和损失）
n_trees = 100
learning_rate = 0.1
for i in range(n_trees):model = DecisionTreeRegressor(max_depth=1)  # 提升model.fit(X, Y)Y = Y - learning_rate * model.predict(X)M.append(model)# print(M)###预测
res = np.zeros(df.shape[0])
for j in range(len(M)):if j == 0:res += M[j]# print(res)else:res += learning_rate * M[j].predict(X)# print(res)
print(res)
y_hat = res
print(r2_score(y, y_hat))

1.3.3 Boosting算法总结

Boosting算法要求基学习器能对特定的数据分布进行学习，这可通过重赋权法(re-weighting)实施，即在训练过程的每一轮中，根据样本分布为每个训练样本重新赋予一个权重。对无法接受带权样本的基学习算法，则可通过重采样(re-sampling)来处理，即在每一轮学习中根据样本分布对训练集重新进行采样，再用重采样而得的样本集对基学习器进行训练。一般而言，这两种做法没有显著的优劣差别。
Boosting算法在训练的每一轮都要检查当前生成的基学习器是否满足基本条件（是否优于随机猜测），一旦条件不满足，则当前基学习器即被抛弃，且学习过程停止——此时，初始设置的学习轮数T也许还远未达到，可能导致最终集成中只包含很少的基学习器而性能不佳。若采用重采样法，则可获得重启动机会以避免训练过程过早停止，即在抛弃不满足条件的当前学习器之后，可根据当前分布重新对训练样本进行采样，再基于新的采样结果重新训练出基学习器，从而使得学习过程可以持续到预设的T轮完成
从偏差-方差分解的角度看，Boosting主要关注降低偏差，因此Boosting能基于泛化性能相当弱的学习器建出很强的集成。
集成的规模(size)指集成中包含的个体学习器数目。