本文主要是介绍2278. 企鹅游行(最大流,拆点),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
活动 - AcWing
在南极附近的某个地方,一些企鹅正站在一些浮冰上。
作为群居动物,企鹅们喜欢聚在一起,因此,它们想在同一块浮冰上会合。
企鹅们不想淋湿自己,所以它们只能利用自己有限的跳跃能力,在一块块浮冰之间跳跃移动,从而聚在一起。
但是,最近的温度很高,浮冰上也有了裂纹。
每当企鹅在一块浮冰上发力跳到另一块浮冰上时,起跳的浮冰都会遭到破坏,落点的浮冰并不会因此受到影响。
当浮冰被破坏到一定程度时,浮冰就会消失。
现在已知每块浮冰可以承受的具体起跳次数。
请帮助企鹅找出它们可以会合的所有浮冰。
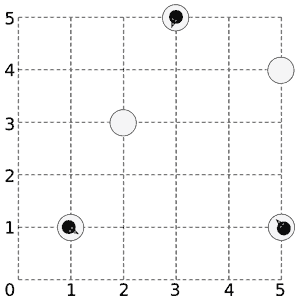
上图是一个浮冰上站着 33 个企鹅的示例图。
输入格式
第一行一个整数 T,表示测试数据数量。
对于每组测试数据:
第一行包含一个整数 N 和一个浮点数 D,表示冰块的数量以及企鹅可以跳跃的最大距离。
接下来 N 行,每行包含四个整数 xi,yi,ni,mi,用来描述一块浮冰的 X 坐标、Y 坐标、该浮冰上站着的企鹅数量以及该浮冰可以承受的起跳次数。
N 块浮冰按照输入的顺序,依次编号为 0∼N−1。
输出格式
对于每组测试数据:
输出占一行,按从小到大的顺序输出所有可以用来会合的浮冰的编号。
如果无法会合,则输出 −1。
数据范围
1≤T≤100,
1≤N≤100,
0≤D≤105,
−10000≤xi,yi≤10000
0≤ni≤10
1≤mi≤200
输入样例:
2
5 3.5
1 1 1 1
2 3 0 1
3 5 1 1
5 1 1 1
5 4 0 1
3 1.1
-1 0 5 10
0 0 3 9
2 0 1 1
输出样例:
1 2 4
-1解析:
拆点:将限制流量的点拆成:出点,入点;两点之间用一条边连接。
这样将点的流量转换成边的流量进行控制。
建图方式:
建立一个虚拟源点 S,连向每个点的每条边的容量==点初始的企鹅数量;枚举每一个点作为汇点 T。
注意事项:
由于是枚举每个点作为汇点 T,因此我们不能在上一次的残留网络上直接跑最大流算法,必须要还原成初始的残留网络。否则,上一次的残留网络中当前的汇点 T 流出的流量将会导致当前图中的流量不守恒。
#include<iostream>
#include<string>
#include<cstring>
#include<cmath>
#include<ctime>
#include<algorithm>
#include<utility>
#include<stack>
#include<queue>
#include<vector>
#include<set>
#include<math.h>
#include<map>
#include<sstream>
#include<deque>
#include<unordered_map>
#include<unordered_set>
#include<bitset>
using namespace std;
typedef long long LL;
typedef unsigned long long ULL;
typedef pair<int, int> PII;
const int N = 210, M =20410 , INF = 0x3f3f3f3f;
int n, S, T;
double D;
int h[N], e[M], f[M], ne[M], idx;
int q[N], d[N], cur[N];
PII p[110];
double eps = 1e-8;void add(int a, int b, int c) {e[idx] = b, f[idx] = c, ne[idx] = h[a], h[a] = idx++;e[idx] = a, f[idx] = 0, ne[idx] = h[b], h[b] = idx++;
}bool check(PII a, PII b) {int x = a.first - b.first, y = a.second - b.second;return x * x + y * y <= D * D + eps;
}bool bfs() {int hh = 0, tt = 0;memset(d, -1, sizeof d);q[0] = S, d[S] = 0, cur[S] = h[S];while (hh <= tt) {int t = q[hh++];for (int i = h[t]; i != -1; i = ne[i]) {int j = e[i];if (d[j] == -1 && f[i]) {d[j] = d[t] + 1;cur[j] = h[j];if (j == T)return 1;q[++tt] = j;}}}return 0;
}int find(int u, int limit) {if (u == T)return limit;int flow = 0;for (int i = cur[u]; i != -1 && flow < limit; i = ne[i]) {int j = e[i];cur[u] = i;if (d[j] == d[u] + 1 && f[i]) {int t = find(j, min(f[i], limit - flow));if (!t)d[j] = -1;f[i] -= t, f[i ^ 1] += t, flow += t;}}return flow;
}int dinic() {int ret = 0,flow;while (bfs())while (flow = find(S, INF))ret += flow;//cout << ret << endl;return ret;
}int main() {int cases = 0;cin >> cases;while (cases--) {memset(h, -1, sizeof h);idx = 0;scanf("%d%lf", &n, &D);S = 0;int tot = 0;for (int i = 1,a,b,c,d; i <= n; i++) {scanf("%d%d%d%d", &a, &b, &c, &d);p[i] = { a,b };add(S, i, c);add(i, i + n, d);tot += c;}for (int i = 1; i <= n; i++) {for (int j = 1; j < i; j++) {if (check(p[i], p[j])) {add(i + n, j, INF);add(j + n, i, INF);}}}int cnt = 0;for (int i = 1; i <= n; i++) {T = i;for (int j = 0; j < idx; j += 2) {f[j] += f[j ^ 1];f[j ^ 1] = 0;}if (dinic() == tot) {printf("%d ", i - 1);cnt++;}}if (!cnt)cout << -1 << endl;else cout << endl;}return 0;
}这篇关于2278. 企鹅游行(最大流,拆点)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




