本文主要是介绍奇偶校验码 、循环冗余校验码(CRC)、 海明码,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
在计算机运行时,为保证二进制数据在传输时准确无误,通常利用校验码来检测并纠错传输的数据。所谓码距就是任意合法编码之间至少有多少个二进制位不同。例如: 码距位1的“8 1 4 2” 码对应的二进制分别是 1000,0001,0100,0010. ,当其中一个编码二进制位发生了变化,还是满足码距为1的合法编码。所以,单纯靠码距并不能检验出传输内容中的错误。
一、奇偶校验码
在编码中增加一位校验位来使编码中的1的个数为奇数或者为偶数,从而使码距变为2.奇校验就是加上校验位来使编码中的1的个数为奇数,偶校验就是加上校验位来使编码中的1的个数为偶数。
例如 对于编码8,对应的原字节流 是 00001000 .在顶部加上校验位,奇校验的话字节流就成了 0 00001000 ,
| 原码 | 0 00001000 | 编码正确 |
| 其中一个bit传输错误 | 0 00001010 | 不满足1的个数为奇数 |
| 其中两个bit传输错误 | 0 00101010 | 编码正确,满足1的个数为奇数 |
| 其中三个bit传输错误 | 0 00001111 | 不满足1的个数为奇数 |
对于偶校验
| 原码 | 1 00001000 | 编码正确 |
| 其中一个bit传输错误 | 1 00001010 | 不满足1的个数为偶数 |
| 其中两个bit传输错误 | 1 00101010 | 编码正确,满足1的个数为偶数 |
| 其中三个bit传输错误 | 1 00001111 | 不满足1的个数为偶数 |
所以奇偶校验码,不能检测偶数个bit传输错误的情况,也不能对错误bit进行纠正。
二、循环冗余校验码(CRC)
CRC采用生成多项式对源码进行校验,在源码的尾数加上校验位。在校验计算中,采用源码和比多项式码少一位的零码组成,对多项式码进行模2运算,就是异或。得到的余数就是校验位。
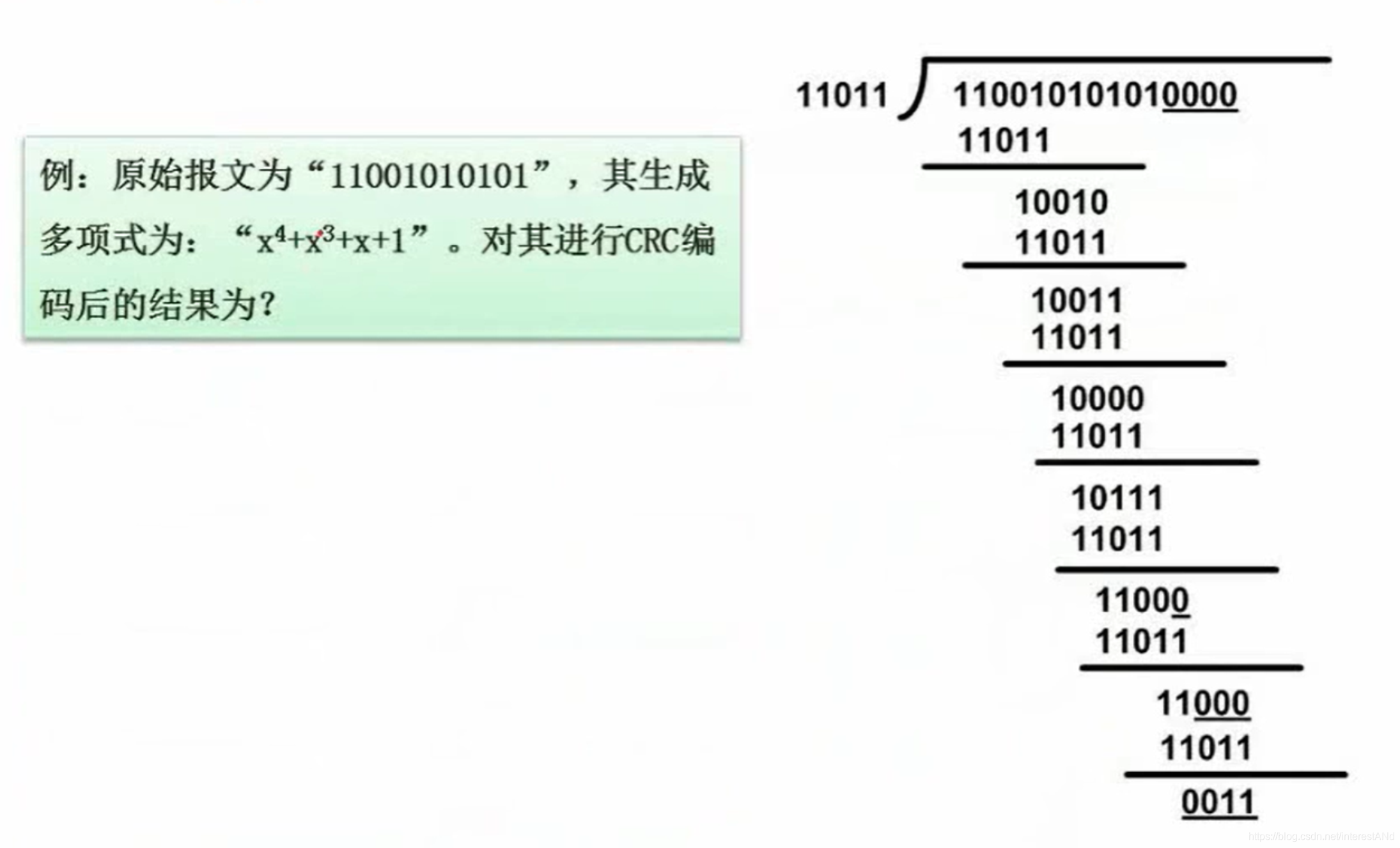
例如生成多项式式 X^4+X^3+0*X^2+X+1 对应的多项式编码码 11011.为五位,那么在校验过程中对原报文加上四个零,然后进行模2运算得到最终的余数。就是校验码。发送的最终报文就是:
110010101010011
三、海明码
海明码在数据之中的特定位置上插入k个校验位。数据位数为n。那么海明码的总位数就是n+k
插入的个数满足 2^k -1 >= n+k
1)插入的校验位Pi = 2^(i-1)位置,即海明码的 1,2,4,8,16,32.....bit位
2)对海明码bit的下标分别转成二进制数,再把校验位对应的海明码bit,的零替换成通配符得到分组。
例如 8 位的数据为,4位的校验位
| 校验位下标零替换成通配符 | 1*** | *1** | **1* | ***1 | ||||||||
| 海明码 | H12 | H11 | H10 | H9 | H8 | H7 | H6 | H5 | H4 | H3 | H2 | H1 |
| 数据位D/校验位P | D7 | D6 | D5 | D4 | P4 | D3 | D2 | D1 | P3 | D0 | P2 | P1 |
- 满足****1的的海明码下标分别是 H1,H3,H5,H7,H9,H11 ,所以对应的 P1,D0,D1,D3,D4,D6 为一组
- 满足***1*的的海明码下标分别是 H2,H3,H6,H7,H10,H11,所以对应的 P2,D0,D2,D3,D5,D6 为一组
- 同理 P3,D1,D2,D3,D7为一组
- P4,D4,D5,D6,D7为一组
3)对每个分组分别作亦或运算⊕ ,本别道道检验结果Gi ,当偶校验时,每个检验结果都为0,则无异常;当奇校验时,每个检验结果都为1,则无异常.
4)如果Gi不为全0时,对应的十进制数则说明海明码对应的下标出错。取反可纠正。
例如:1001001110序列,10位
1)需插入4个校验位,海明码共14位,海明码对应的内容如下表
| 校验位下标零替换成通配符 | *1*** | **1** | ***1* | ****1 | ||||||||||
| 海明码 | H14 | H13 | H12 | H11 | H10 | H9 | H8 | H7 | H6 | H5 | H4 | H3 | H2 | H1 |
| 数据位D/校验位P | D9 | D8 | D7 | D6 | D5 | D4 | P4 | D3 | D2 | D1 | P3 | D0 | P2 | P1 |
| 奇校验 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 |
| 偶校验 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 |
| 实际接收到的值 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 0 |
2)分组
P1,D0,D1,D3,D4,D6,D8 为一组;
P2,D0,D2,D3,D5,D6,D9为一组;
P3,D1,D2,D3,D7,D8,D9为一组;
P4,D4,D5,D6,D7,D8,D9为一组;
4)求P的值,假如是偶校验 //1001001110
P1=D0⊕D1⊕D3⊕D4⊕D6⊕D8 =0 ⊕1 ⊕1 ⊕ 0 ⊕ 1⊕ 0 =1
P2=D0⊕D2⊕D3⊕D5⊕D6⊕D9 =0 ⊕1 ⊕1 ⊕ 0 ⊕ 1⊕ 1 =0
P3=D1⊕D2⊕D3⊕D7⊕D8⊕D9 = 1⊕1 ⊕1 ⊕ 0 ⊕0⊕ 1 =0
P4 = D4⊕D5⊕D6⊕D7⊕D8,⊕D9 = 0⊕0 ⊕1 ⊕ 0 ⊕0⊕ 1 =0
3)对实际接收到的值作亦或 ,
G1 = P1⊕D0⊕D1⊕D3⊕D4⊕D6⊕D8 =1 ⊕0 ⊕1 ⊕1 ⊕ 0 ⊕ 1⊕ 0 = 0
G2 = P2⊕D0⊕D2⊕D3⊕D5⊕D6⊕D9 = 0⊕0 ⊕0 ⊕1 ⊕ 0 ⊕ 1⊕ 1 = 1
G3 =P3⊕D1⊕D2⊕D3⊕D7⊕D8⊕D9 = 0⊕1⊕0 ⊕1 ⊕ 0 ⊕0⊕ 1 =1
G4 = P4 ⊕D4⊕D5⊕D6⊕D7⊕D8,⊕D9 =0⊕0⊕0 ⊕1 ⊕ 0 ⊕0⊕ 1 =0
所以 对应的 G4 G3 G2 G1 的值收 0110 真值为6 ,以为着H6传输发生错误,即D2发生错误,取反修正即可。
这篇关于奇偶校验码 、循环冗余校验码(CRC)、 海明码的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




