本文主要是介绍漫漫数学之旅032,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!

文章目录
- 经典格言
- 数学习题
- 古今评注
- 名人小传
经典格言
数学天才与艺术天才彼此灵犀相通。——哥斯塔·米塔格·勒弗莱(Gösta Mittag-Leffler)
哥斯塔·米塔格·勒弗莱,这位数学界的“大魔法师”,曾用他那根智慧的魔杖揭示了数学与艺术之间一条隐形的魔法通道。他说,“数学天才和艺术天才呀,他们就像是两个平行宇宙中的超级英雄,虽然各自守护着不同的领地——一个在精准无误的逻辑王国里绘制完美的几何图形,另一个则在情感洋溢的艺术殿堂挥洒灵感色彩——但他们却能在神秘的心灵感应中找到彼此。”
想象一下这样的情景:数学家就像一位擅长精密构造迷宫的智者,在坐标轴上舞动着公式和定理的音符,创作出一首首无声的交响乐;而艺术家呢,则是一位能够驾驭光影与色彩的大师,用画笔描绘出流动的曲线和无限空间,那些画面似乎都暗含着黄金分割的韵律。
每当数学家解开一个复杂难题时,就如同艺术家完成一幅传世之作般激动人心;而当画家捕捉到抽象美感的一刹那,也犹如数学家找到了那个隐藏在数列背后的优美规律。这两类看似迥异的天才其实都在追求一种普遍真理的表达,只不过一个用的是数字语言,一个用的是视觉语言,但他们都能创造出令人叹为观止的美。
所以,不妨把这句名言理解为:“嘿,伙计们,甭管你是算得一手好π还是画得出梵高的星空,只要心中有爱、脑中有光,咱们都是为了追寻那份跨越维度的理解与创造之美。”如此一来,数学天才和艺术天才不仅灵犀相通,还可能在某个深夜茶话会上,共享一块芝士蛋糕,一起探讨如何用微积分解析印象派色彩的变化呢!
数学习题
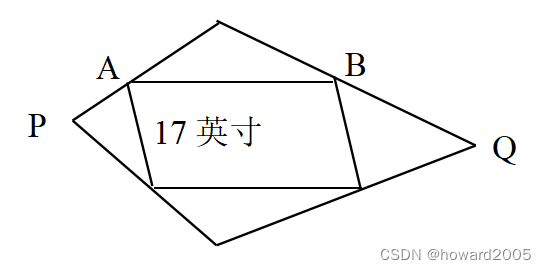
已知大四边形各边的中点是小四边形的顶点,|PQ|=46,求|AB|。
古今评注
在那奇妙且充满神秘色彩的数学世界里,我们的故事主角并不是什么哈利波特式的魔法学院学生,而是来自东京大学气候系统研究中心和日本国家环境研究所的一群“气象巫师”和“环保算法师”。他们可不是普通的天文学家或化学家,而是一群掌握着深奥数学符咒的大师,他们的目标是揭示全球变暖背后的秘密,并用他们的智慧之笔绘制出地球气候系统的奇幻画卷。
这群科学家们联手构建了一个可以媲美“霍格沃茨气候模拟器”的神奇模型。这个模型堪称是一个精密复杂的气候魔方,它不仅包含了微粒们在大气中的“粒子舞会”,还精确计算了这些小家伙们的化学变身大戏。就像《冰雪奇缘》中艾莎女王操控冰雪那样,他们利用数学法则掌控着风儿吹拂、雨水冲刷以及季节更替对那些飘浮于空中的微粒产生的影响。
这个模型可不只是纸上谈兵的理论之作,它与卫星这位忠实的“天空侦探”合作了一年多的时间,密切监视并记录下了大气中微粒的实际分布情况。这就好比给每个微粒都配备了GPS定位器,让它们在浩瀚的宇宙舞台上表演了一场生动逼真的现实版《天气之子》。
经过无数次迭代运算与数据校验,这一魔法般的数学模型最终修炼成精,不仅能精准预测气候变化趋势,还能在某种程度上预知未来地球可能面临的温度挑战。这个强大的工具仿佛是一部科幻小说里的时光机,只不过它带我们探索的是未来的气候变迁,而非过去的历史长河。
总结来说,这群以数学为剑、以科学为盾的研究者们,通过他们精心打造的模型,在全球变暖这场没有硝烟的战役中,用幽默而又严谨的方式向我们展示了数学如何在全球气候变化研究领域扮演着举足轻重的角色,同时也让我们对未来充满了好奇与期待,毕竟,谁不想知道数学会如何帮助我们解开地球母亲的绿色密码呢?
名人小传

哥斯塔·米塔格·勒弗莱(Gösta Mittag-Leffler,1846年3月16日-1927年7月7日),这位数学界的显赫人物,被喻为瑞典数学的“太阳王”,在数学领域里光芒四射。他不仅是个杰出的数学家,更是个卓越的学术组织者和出版人,以其创办的《Acta Mathematica》期刊而闻名于世,该刊成为了当时及后世顶尖数学研究成果的重要发布平台。
关于他与诺贝尔奖不设数学奖之间的传说,坊间流传着许多富有幽默色彩却不太靠谱的故事。其中最八卦的一个版本是说,诺贝尔因为个人恩怨或情感纠葛而故意避开设立数学奖。传言绘声绘色地描述了米塔格-勒弗莱作为诺贝尔的情敌或者是因为其他私人原因导致诺贝尔对数学家们怀恨在心。然而,这些都只是无稽之谈,事实上诺贝尔遗嘱中并未提及数学奖是因为在他那个时代,数学并未像物理学、化学那样直接关联到工业和技术革新,这被认为是更接近诺贝尔本人所关注的实际应用科学范畴。
实际上,诺贝尔生前并未结婚,也没有公开记录表明他与米塔格-勒弗莱存在任何直接的情感纠纷。而且,即使两人之间有任何芥蒂,也无法证实这是诺贝尔未设立数学奖的原因。真正的原因可能更为简单且实际:诺贝尔认为数学的重要性虽然无可争议,但其成果不如物理学、化学等领域的发明那样具有立即可见的社会效益。
所以,下次当你听到有人把诺贝尔不设数学奖归咎于哥斯塔·米塔格·勒弗莱的“魅力攻势”时,不妨一笑置之,毕竟真正的历史往往比小说更加平淡却也更有深度。
这篇关于漫漫数学之旅032的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








