本文主要是介绍密码学系列之:Argon2加密算法详解,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
文章目录
- 简介
- 密钥推导函数key derivation function
- Password Hashing Competition
- Argon2算法
- Argon2的输入参数
- 处理流程
简介
Argon2是一个密钥推导函数,在2015年7月被选为密码哈希大赛的冠军,它由卢森堡大学的Alex Biryukov、Daniel Dinu和Dmitry Khovratovich设计,Argon2的实现通常是以Creative Commons CC0许可(即公共领域)或Apache License 2.0发布,并提供了三个相关版本,分别是Argon2d,Argon2i和Argon2id。
本文将会讨论一下Argon2的原理和使用。
密钥推导函数key derivation function
在密码学中,密钥推导函数(KDF)是一种密码学哈希函数,它使用伪随机函数从一个秘密值(如主密钥、密码或口令)中推导出一个或多个密钥。 KDF可用于将密钥拉伸成更长的密钥,或获得所需格式的密钥,例如将Diffie-Hellman密钥交换的结果转换为用于AES的对称密钥。
Password Hashing Competition
密码学虽然是研究密码的,但是其加密算法是越公开越好,只有公开才能去检视该算法的好坏,只有经过大家的彻底研究,才能够让该算法得以在业界使用和传播。
最出名的密码算法大赛肯定是由NIST在2001年为了指定标准的AES算法举办的大赛,该大赛的目的寻找最新的加密算法来替代老的DES算法。在这次大赛中,涌现了许多优秀的算法,包括CAST-256, CRYPTON, DEAL, DFC, E2, FROG, HPC, LOKI97, MAGENTA, MARS, RC6, Rijndael, SAFER+, Serpent, 和 Twofish等。最终Rijndael算法被选为最终的AES算法实现。
同样的PHC也是一个这样的算法比赛,和NIST举办的算法比赛不同的是,这是一个非官方的,由密码学家们组织的比赛。它是在由Jean-Philippe Aumasson于2012年秋季发起。
2013年第一季度,发布了征集意见书的通知,到2014年3月31日截止日期,共收到24份意见书。2014年12月,确定了9个入围名单。2015年7月,宣布Argon2为优胜者。
Argon2算法
Argon2 的设计很简单,旨在实现最高的内存填充率和对多个计算单元的有效利用,同时还能提供对 tradeoff attacks 的防御(通过利用处理器的缓存和内存)。
Argon2有三个变种。Argon2i、Argon2d和Argon2id。Argon2d速度更快,并且使用数据依赖的内存访问方式,这使得它对GPU破解攻击有很强的抵抗力,适合没有side-channel timing attacks威胁的应用(例如加密货币)。
Argon2i则使用数据无关的内存访问,这对于密码哈希和基于密码的密钥推导算法来说是首选,其特点是速度较慢,因为它在内存上运行了更多的处理逻辑,以防止 tradeoff attacks 。
Argon2id是Argon2i和Argon2d的混合体,采用数据依赖型和数据独立型内存访问相结合的方式,从而可以同时抵御side-channel timing attacks和GPU破解攻击的能力。
Argon2的输入参数
Argon2有两类输入参数,分别是primary inputs和secondary inputs。
primary inputs包括要加密的消息P和nonce S,分别代表password和salt。
P的长度是0到232-1字节,S的长度是8到232-1字节(如果是做密码hash,推荐16字节)。
之所以叫做primary inputs,是因为这两个参数是必须输入的。
剩下的参数叫做secondary inputs,他们包括:
- 并行程度p,表示同时可以有多少独立的计算链同时运行,取值是1到224-1。
- Tag长度 τ, 长度从4到232-1字节。‘
- 内存大小 m, 单位是兆,值取 8p到232-1。
- 迭代器的个数t,提升运行速度。取值1到232-1。
- 版本号v,一个字节,取值0x13。
- 安全值 K , 长度是0到232-1字节。
- 附加数据 X,长度是0到232-1字节。
- Argon2的类型,0代表Argon2d,1代表Argon2i,2代表Argon2id。
这些输入可以用下面的代码来表示:
Inputs:password (P): Bytes (0..232-1) Password (or message) to be hashedsalt (S): Bytes (8..232-1) Salt (16 bytes recommended for password hashing)parallelism (p): Number (1..224-1) Degree of parallelism (i.e. number of threads)tagLength (T): Number (4..232-1) Desired number of returned bytesmemorySizeKB (m): Number (8p..232-1) Amount of memory (in kibibytes) to useiterations (t): Number (1..232-1) Number of iterations to performversion (v): Number (0x13) The current version is 0x13 (19 decimal)key (K): Bytes (0..232-1) Optional key (Errata: PDF says 0..32 bytes, RFC says 0..232 bytes)associatedData (X): Bytes (0..232-1) Optional arbitrary extra datahashType (y): Number (0=Argon2d, 1=Argon2i, 2=Argon2id)Output:tag: Bytes (tagLength) The resulting generated bytes, tagLength bytes long
处理流程
我们先来看一下非并行的Argon2的算法流程:
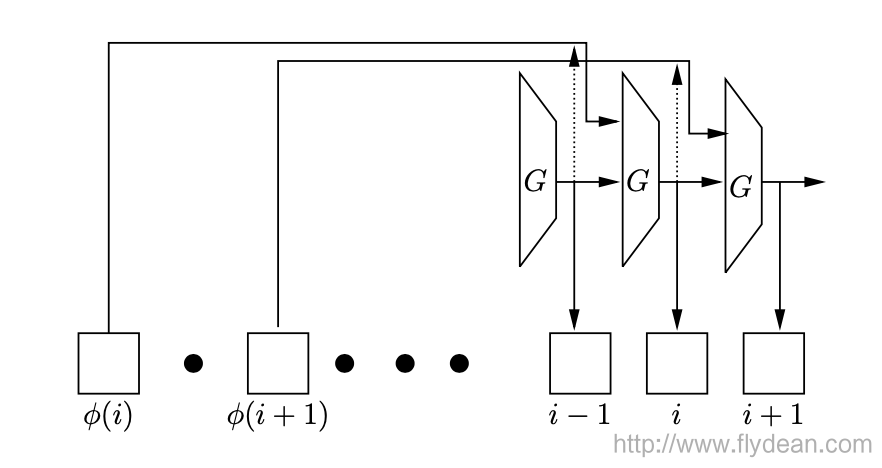
非并行的Argon2是最简单的。
上图中G表示的是一个压缩函数,接收两个1024byte的输入,输出一个1024byte。
i表示的是执行的步数,上面的φ(i) 就是输入,取自内存空间。
作为一个memory-hard的算法,一个很重要的工作就是构建初始内存。接下来,我们看一下如何构建初始内存空间。
首先,我们需要构建 H0 ,这是一个 64-byte 的block值,通过H0,可以去构建更多的block。计算H0的公式如下:
H0 = H(p,τ,m,t,v,y,⟨P⟩,P,⟨S⟩,S,⟨K⟩,K,⟨X⟩,X)
它是前面我们提到的输入参数的H函数。H0的大小是64byte。
看下H0的代码生成:
Generate initial 64-byte block H0.All the input parameters are concatenated and input as a source of additional entropy.Errata: RFC says H0 is 64-bits; PDF says H0 is 64-bytes.Errata: RFC says the Hash is H^, the PDF says it's ℋ (but doesn't document what ℋ is). It's actually Blake2b.Variable length items are prepended with their length as 32-bit little-endian integers.buffer ← parallelism ∥ tagLength ∥ memorySizeKB ∥ iterations ∥ version ∥ hashType∥ Length(password) ∥ Password∥ Length(salt) ∥ salt∥ Length(key) ∥ key∥ Length(associatedData) ∥ associatedDataH0 ← Blake2b(buffer, 64) //default hash size of Blake2b is 64-bytes
对于输入参数并行程度p来说,需要将内存分成一个内存矩阵B[i][j], 它是一个 p 行的矩阵。
计算矩阵B的值:

其中H′ 是一个基于H的变长hash算法。
我们给一下这个算法的实现:
Function Hash(message, digestSize)Inputs:message: Bytes (0..232-1) Message to be hasheddigestSize: Integer (1..232) Desired number of bytes to be returnedOutput:digest: Bytes (digestSize) The resulting generated bytes, digestSize bytes longHash is a variable-length hash function, built using Blake2b, capable of generatingdigests up to 232 bytes.If the requested digestSize is 64-bytes or lower, then we use Blake2b directlyif (digestSize <= 64) thenreturn Blake2b(digestSize ∥ message, digestSize) //concatenate 32-bit little endian digestSize with the message bytesFor desired hashes over 64-bytes (e.g. 1024 bytes for Argon2 blocks),we use Blake2b to generate twice the number of needed 64-byte blocks,and then only use 32-bytes from each blockCalculate the number of whole blocks (knowing we're only going to use 32-bytes from each)r ← Ceil(digestSize/32)-1;Generate r whole blocks.Initial block is generated from messageV1 ← Blake2b(digestSize ∥ message, 64);Subsequent blocks are generated from previous blocksfor i ← 2 to r doVi ← Blake2b(Vi-1, 64)Generate the final (possibly partial) blockpartialBytesNeeded ← digestSize – 32*r;Vr+1 ← Blake2b(Vr, partialBytesNeeded)Concatenate the first 32-bytes of each block Vi(except the possibly partial last block, which we take the whole thing)Let Ai represent the lower 32-bytes of block Vireturn A1 ∥ A2 ∥ ... ∥ Ar ∥ Vr+1
如果我们的迭代次数多于一次,也就是说t > 1, 我们这样计算下一次迭代的 B :
B t [ i ] [ 0 ] = G ( B t − 1 [ i ] [ q − 1 ] , B [ i ′ ] [ j ′ ] ) ⊕ B t − 1 [ i ] [ 0 ] B^{t}[i][0]=G\left(B^{t-1}[i][q-1], B\left[i^{\prime}\right]\left[j^{\prime}\right]\right) \oplus B^{t-1}[i][0] Bt[i][0]=G(Bt−1[i][q−1],B[i′][j′])⊕Bt−1[i][0]
B t [ i ] [ j ] = G ( B t [ i ] [ j − 1 ] , B [ i ′ ] [ j ′ ] ) ⊕ B t − 1 [ i ] [ j ] B^{t}[i][j]=G\left(B^{t}[i][j-1], B\left[i^{\prime}\right]\left[j^{\prime}\right]\right) \oplus B^{t-1}[i][j] Bt[i][j]=G(Bt[i][j−1],B[i′][j′])⊕Bt−1[i][j]
最终遍历T次之后,我们得到最终的B :
B final = B T [ 0 ] [ q − 1 ] ⊕ B T [ 1 ] [ q − 1 ] ⊕ ⋯ ⊕ B T [ p − 1 ] [ q − 1 ] B_{\text {final }}=B^{T}[0][q-1] \oplus B^{T}[1][q-1] \oplus \cdots \oplus B^{T}[p-1][q-1] Bfinal =BT[0][q−1]⊕BT[1][q−1]⊕⋯⊕BT[p−1][q−1]
最后得到输出:
T a g ← H ′ ( B final ) \mathrm{Tag} \leftarrow H^{\prime}\left(B_{\text {final }}\right) Tag←H′(Bfinal )
这段逻辑也可以用代码来表示:
Calculate number of 1 KB blocks by rounding down memorySizeKB to the nearest multiple of 4*parallelism kibibytesblockCount ← Floor(memorySizeKB, 4*parallelism)Allocate two-dimensional array of 1 KiB blocks (parallelism rows x columnCount columns)columnCount ← blockCount / parallelism; //In the RFC, columnCount is referred to as qCompute the first and second block (i.e. column zero and one ) of each lane (i.e. row)for i ← 0 to parallelism-1 do for each rowBi[0] ← Hash(H0 ∥ 0 ∥ i, 1024) //Generate a 1024-byte digestBi[1] ← Hash(H0 ∥ 1 ∥ i, 1024) //Generate a 1024-byte digestCompute remaining columns of each lanefor i ← 0 to parallelism-1 do //for each rowfor j ← 2 to columnCount-1 do //for each subsequent column//i' and j' indexes depend if it's Argon2i, Argon2d, or Argon2id (See section 3.4)i′, j′ ← GetBlockIndexes(i, j) //the GetBlockIndexes function is not definedBi[j] = G(Bi[j-1], Bi′[j′]) //the G hash function is not definedFurther passes when iterations > 1for nIteration ← 2 to iterations dofor i ← 0 to parallelism-1 do for each rowfor j ← 0 to columnCount-1 do //for each subsequent column//i' and j' indexes depend if it's Argon2i, Argon2d, or Argon2id (See section 3.4)i′, j′ ← GetBlockIndexes(i, j)if j == 0 then Bi[0] = Bi[0] xor G(Bi[columnCount-1], Bi′[j′])elseBi[j] = Bi[j] xor G(Bi[j-1], Bi′[j′])Compute final block C as the XOR of the last column of each rowC ← B0[columnCount-1]for i ← 1 to parallelism-1 doC ← C xor Bi[columnCount-1]Compute output tagreturn Hash(C, tagLength)
本文已收录于 http://www.flydean.com/40-argon2/
最通俗的解读,最深刻的干货,最简洁的教程,众多你不知道的小技巧等你来发现!
欢迎关注我的公众号:「程序那些事」,懂技术,更懂你!
这篇关于密码学系列之:Argon2加密算法详解的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





