本文主要是介绍陕西黑布林滞销只是一篇营销广告,炒作夸大背后多是利益,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
背景
前些天,在朋友圈看到几位好友共同推荐一篇文章,内容是陕西大荔县大量待销黑布林,开始以为是一个营销广告,就像很多卖蜂蜜、卖茶叶的营销文,但文章内有当地政府的盖章,而且文章末尾有“掌上高铁”的公众号,而该公众号的百度百科信息为铁道部的产品,于是信以为真后下单买了10斤布林,其实就算不拿农民卖苦情戏,这个价格跟超市比确实便宜,我也有可能买。
可是,最近发现几位身边的朋友都买了,然后几乎都是通过同一篇文章,感觉事情蹊跷后做了一点小调研,发现果真是一个营销套路,只是通过欺骗来博取同情的销售让人特别不爽,也许很快就把群众的爱心消耗殆尽,也许之后很难轻易相信,哪怕是官方媒体,就像报纸上的内容也要带着脑子去读,就像看到有人跌倒也不敢上去帮忙,就像看到有人乞讨也不再会施舍。
事实依据
自己的结论并没有完全绝对的强因果关系,只是自己的个人判断,展示给各位自己判断,从一下几个角度进行展示证据。
故事真实性存疑
故事中的农民的情况,据多方考证,跟文章所述并不一致。
首先,文章中的孔大哥的个人情况并不一致(上官网新闻)。
其次,大荔县农业农村局自己可能都不知当地有大量严重黑布林滞销情况(都市现场新闻),盖章单位是大荔县商务局,在写当前文章时一直无法与该单位取得联系,我猜这个文件大概率是真实的。
最后,当地政府并不认可滞销的说法,只是表示在农产品统一上市的季节,阶段性难卖是正常现象(西部网新闻)。
官方公信力不足
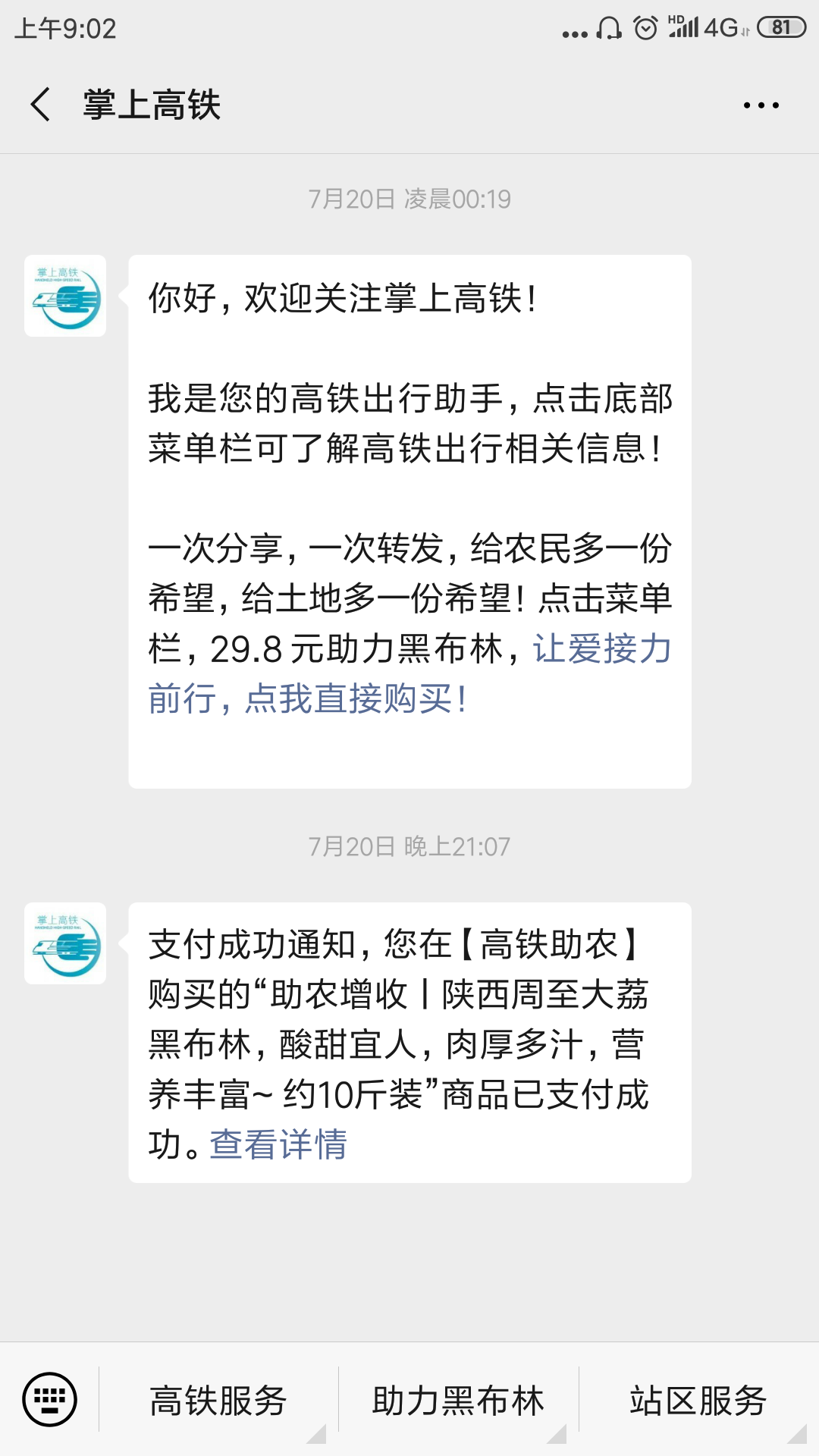
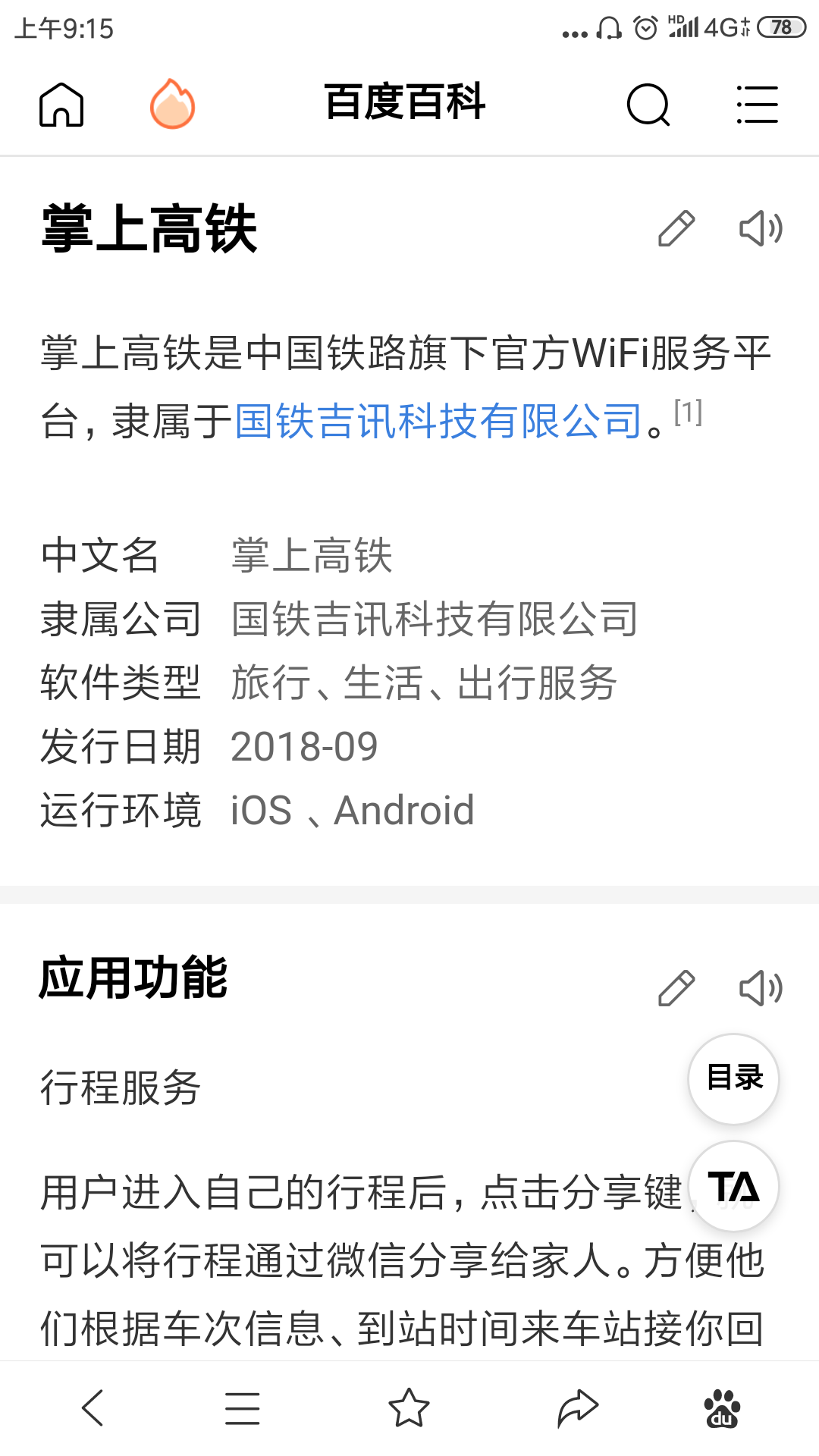
尽管有很多自媒体推广,但本人开始相信故事主要是因为掌上高铁将该信息作为主菜单来推荐。网上资料对于掌上高铁的描述为国铁吉讯科技有限公司产品,该公司成立于2018年7月5日,由中国铁路投资有限公司、吉利、腾讯携手组建成立。
12306官网并没有找到任何关于掌上高铁的信息,而且12306有自己的手机app,叫铁路12306,在12306官网有明确提示:“目前铁路未授权其他网站或APP开展类似服务内容,敬请广大用户注意”。
个人猜测
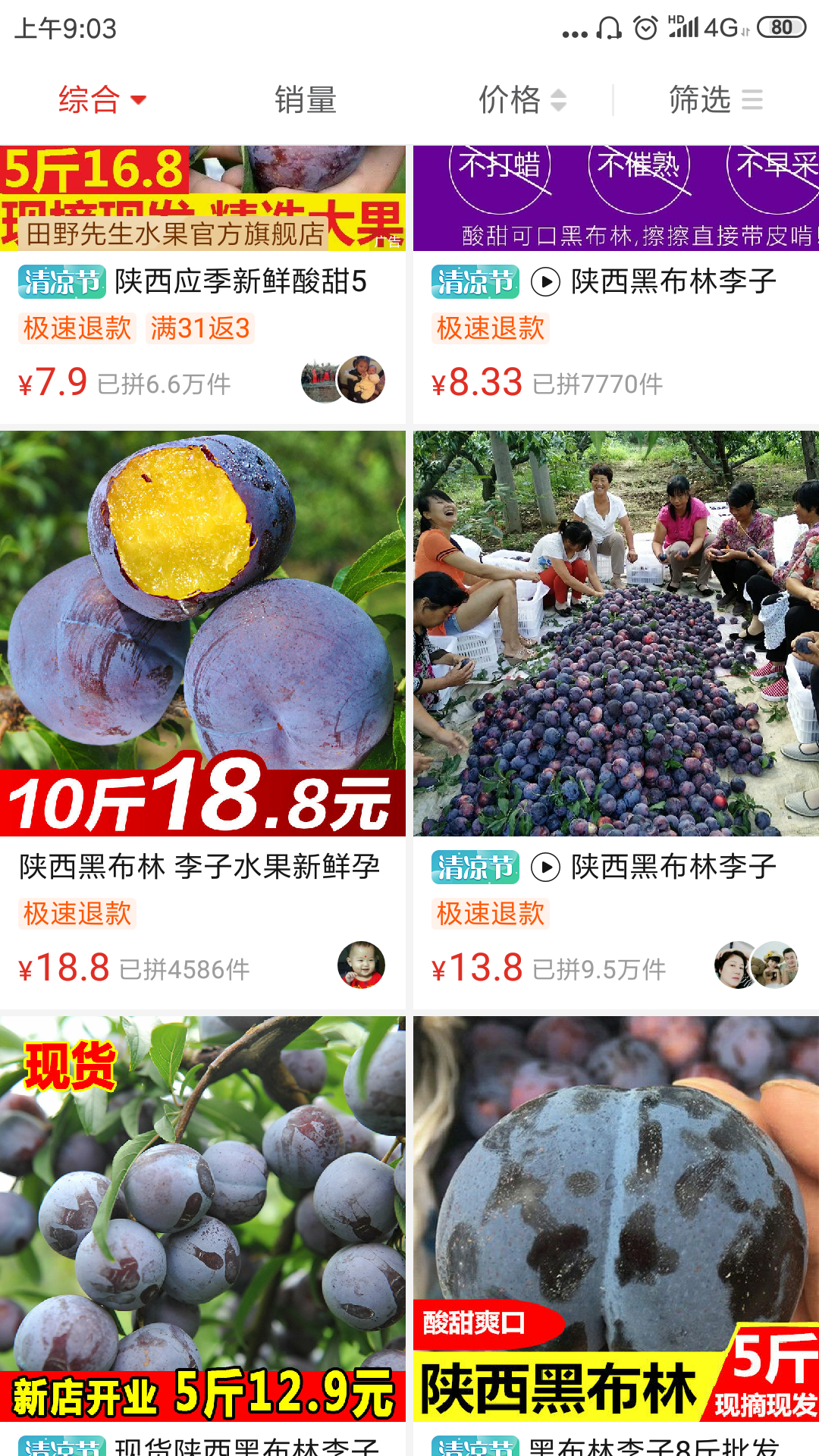
个人猜测都是利益驱使,一方面在掌上高铁的菜单内有个商务合作,是可以联系进行广告投放的;另一方面,营销号很多是给钱就推广的,并不会做太多真实性调研,就好象明星接广告一样,并非每个明星都会试用产品;最后,通过在农民出以1元的价格收取产品,再进行转卖也是可以获利,因为当前时间在拼多多搜索黑布林大多9.9元5斤,18.9元10斤,而文章中的价格是28.9元10斤(超市3-5元每斤)。
如果只是出于好心帮农民卖点水果,完全可以如实陈述,尽管销售效果可能会相对弱势,玩弄感情招摇行骗不仅是伤害消费者的同情心,也是对农民群体信用的摧毁。现在英国新首相鲍里斯·约翰逊在职业生涯早期,只是因为杜撰了一位被采访人的一句话就被泰唔士报开除。
个人呼吁
对于影响国计民生的话题或者事件,需要有一定的约束力。或通过法制方式,或通过舆论方式,而不是任由利益追逐者玩弄社会良知。
现在路上遇到有人摔倒,我还是希望可以无所顾忌的搀扶,而不用担心会被碰瓷;如果网上遇到有人募捐,我还是希望可以心无杂念的捐赠,而不用怀疑物资的去向;如果遇到公权机构发布政策,我还是希望可以坦坦荡荡的接受,而不用思考上层建筑的利益勾结。
这篇关于陕西黑布林滞销只是一篇营销广告,炒作夸大背后多是利益的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!









