西风的数据结构教程（3）——二叉树

本文主要是介绍西风的数据结构教程（3）——二叉树，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

今天我们终于要说到计算机界的经典数据结构——树，树是非常良好的一种组织数据的形式，在现实生活中也经常用到。

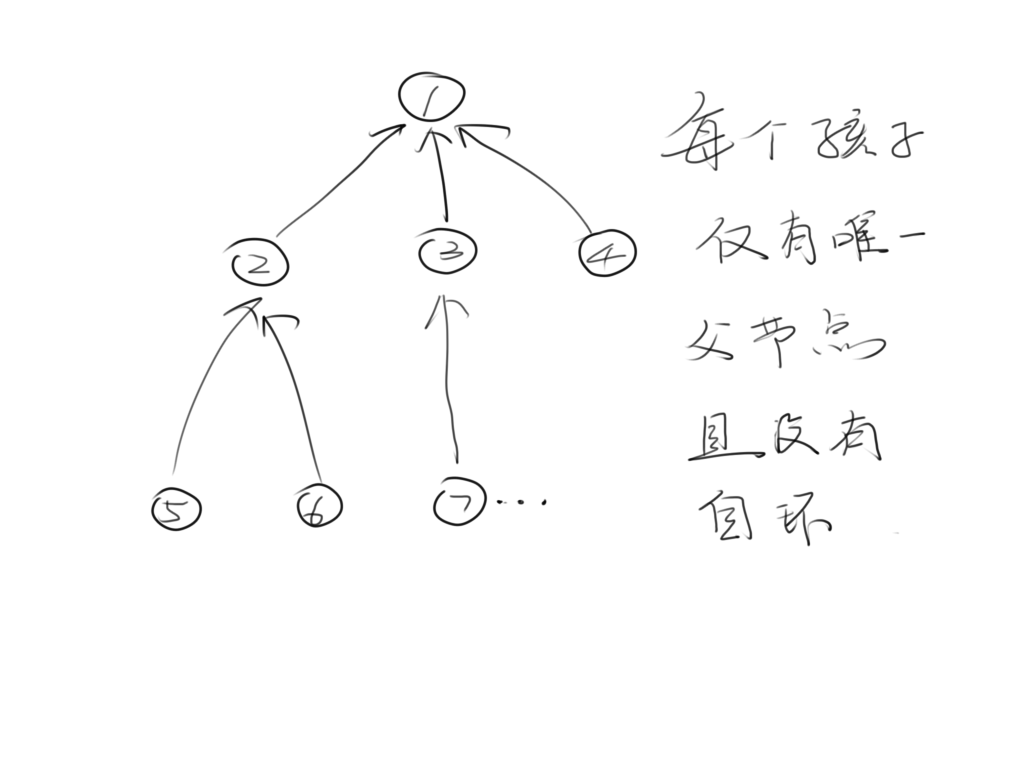
树的结构，大概就是这个样子：

一群树就会组成一个森林

不过，这样并不好管理，所以我们一般会还是使用一个根节点来管理它们。

树结构最大的特点就是，一个节点的情况分析只和父节点和子节点相关，这样管理数据时往往不需要考虑很多。

例如文件系统中，每个文件夹可以视为一个节点，而每个文件夹只显示自己的子节点，结构就非常清晰了。

而二叉树是树结构中的非常常用的一种，往往被用作排序树使用，可以自动排序和判重，可以作为索引使用。

下面我们就来实际写一个二叉排序树，然后增加其平衡性，将其改写为一棵红黑树，不过红黑树的部分十分复杂，可以循序渐进的来学习和理解，不必一下就学习完。

二叉排序树

二叉排序树是简单的排序数据结构，可以支持动态的插入删除数据，对数据快速查找，复杂度只有log(n)

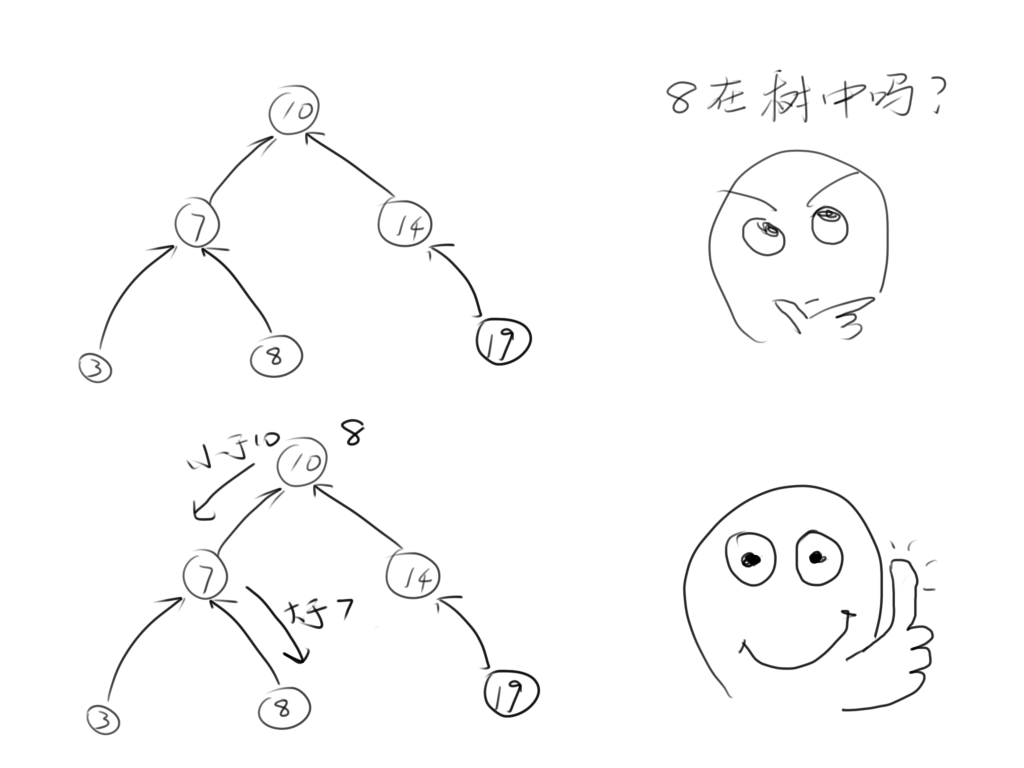
它的实现方法是这样的：

原理很简单，对于每一棵子树，左孩子都比自己小，右孩子都比自己大，那么就利用二分的思想，不断寻找这个数所在的位置。

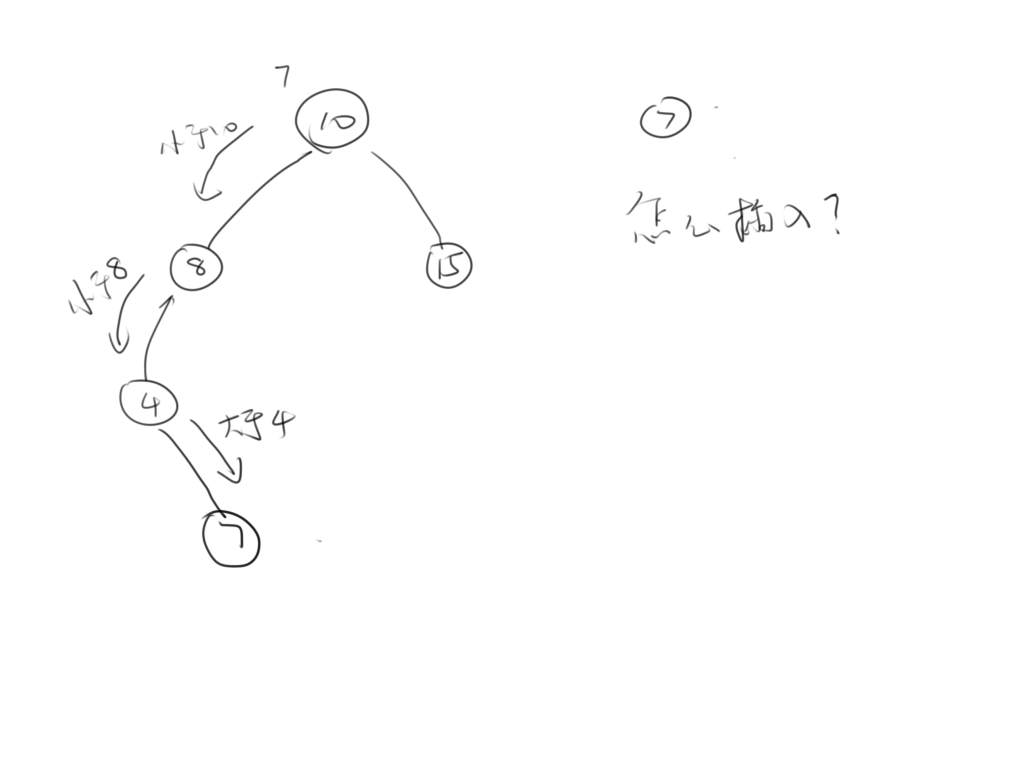
插入时，则需要先考虑好要插入的位置：

我们发现，插入操作和查找操作是几乎一样的，只要找到对应的位置，插入很好办。

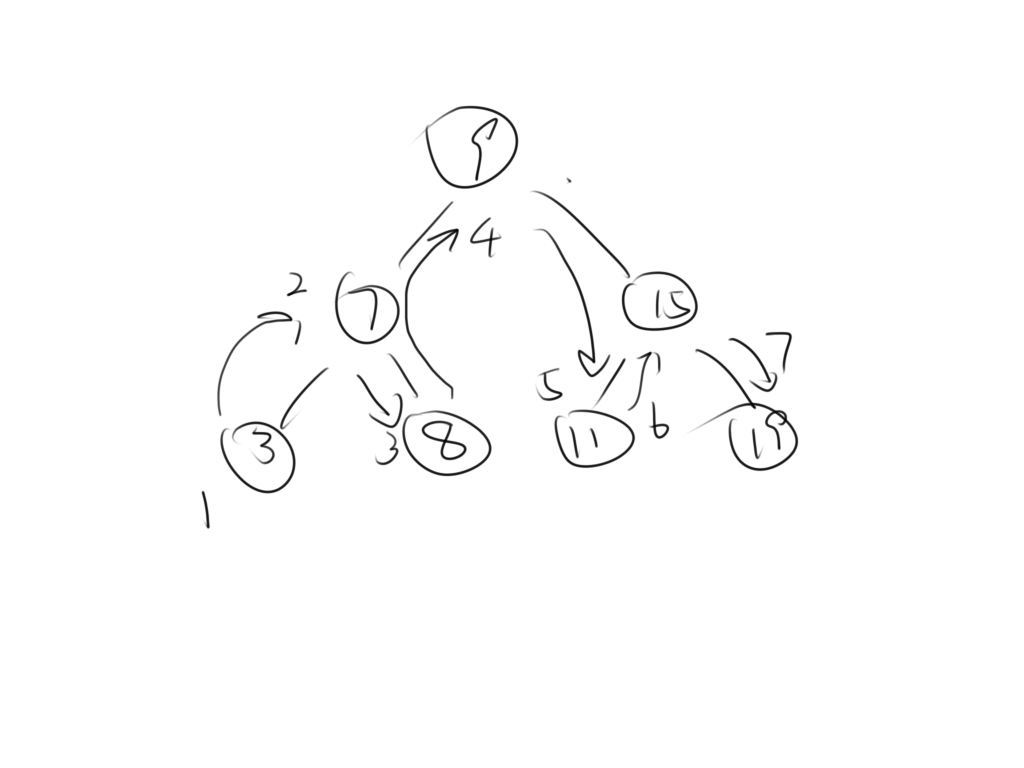
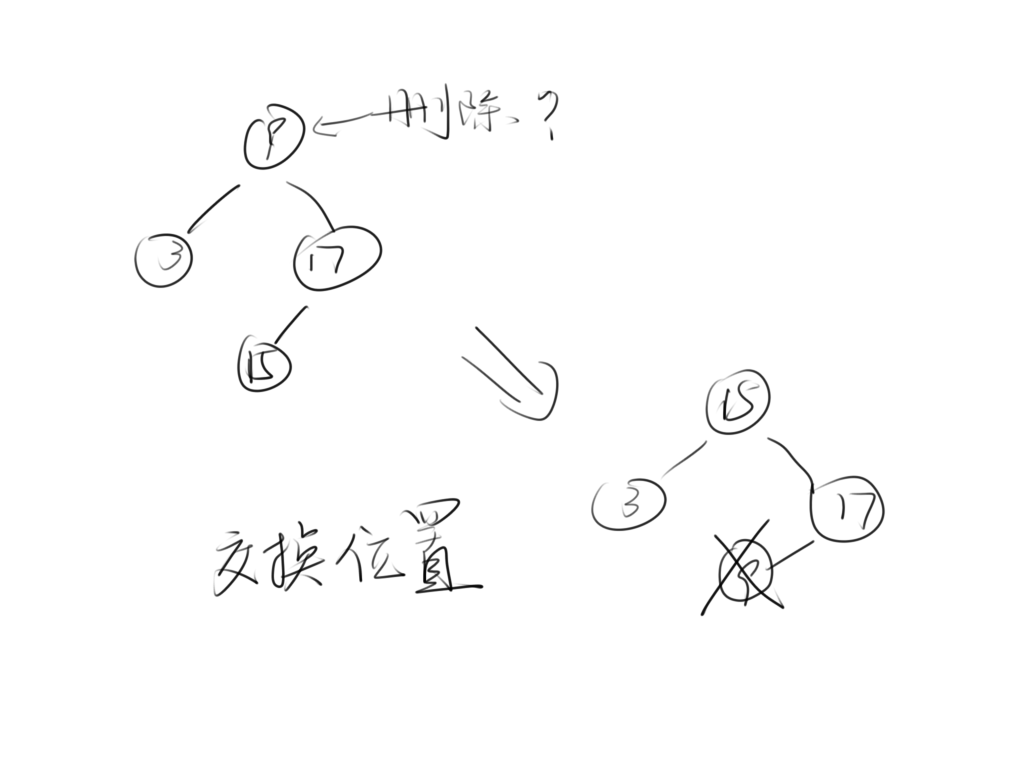
删除时，确实要复杂一点，因为我们直接将节点从树上拿走，如果叶子节点还好办，但我们考虑非叶子节点的删除，就较为复杂了。那么，如何才能正确的删除一个节点呢？我们来观察一下：

通过这张图，我们能看出来，每一个元素的上一个相邻元素是左子树的最右边孩子，下一个元素是右子树的最左孩子，这两个相邻元素都是叶子节点，而且如果左子树没有右孩子节点，那么就用最大的根节点替换。同理，用右子树删除也可以。

那好，我们既然知道了树的基本操作，就来简要的模拟一下，二叉排序树是如何运作的。

二叉排序树的实现

让我们来定义一棵树吧

typedef int TreeElementType;typedef struct _bst_node
{TreeElementType data;struct _bst_node *left, *right;
} bst_node;typedef struct _tree
{bst_node* root;
} bstree;

还是类似的方法，bstree存抽象的树对象，bst_node则是树的每个节点，其中存放的元素单独定义出来

为其编写构造函数：

bst_node* TreeNodeCreate() {bst_node* n = (bst_node*) malloc(sizeof(bst_node));n->left = n->right = NULL;
}bstree* BSTreeCreate() {return (bstree*)malloc(sizeof(bstree));
}

下面我们要开始实现这个二叉树了，二叉树的插入十分简单，只需要递归的判断，当前节点是比中值大还是小，如果小就往左走，大就往右走，相同时就直接返回无法插入即可。
但这样实现考虑到函数的调用效率问题，我们采用while循环来实现，只需要用指针模拟两个节点即可：

void TreeInsert(bstree* t, TreeElementType data) {if (t->root == NULL) { t->root = TreeNodeCreate();t->root->data = data; return;}bst_node* p = t->root;bst_node* q = NULL;while(p != NULL) {if (data < p->data) { q = p; p = p->left; continue; }if (data > p->data) { q = p; p = p->right; continue; }if (data ==p->data) return;}bst_node* node = TreeNodeCreate();node->data = data;if (data < q->data)q->left = node;elseq->right = node;
}

而查找方法也将是使用循环实现的：

bst_node* TreeSearch(bstree* t, TreeElementType data) {if (t->root == NULL) return NULL;bst_node* p = t->root;while(p != NULL) {if (data ==p->data) return p;if (data < p->data) { p = p->left; continue; }if (data > p->data) { p = p->right; continue; }}return NULL;
}

二叉树的删除是最复杂的部分，核心思路就是找一个可以和当前节点互换的元素，将那个元素替换上去，当前节点拿下来：

void TreeDelete(bstree* t, TreeElementType data) {if (t->root == NULL) return;bst_node* p = t->root;bst_node* q = NULL;while(p != NULL) {if (data ==p->data) break;if (data < p->data) { q = p; p = p->left; continue; }if (data > p->data) { q = p; p = p->right; continue; }}if (p == NULL) return;if (p->left == NULL) { // 若p没有左孩子,直接用它的右孩子取代q->right = p->right;Free(p);} else { // 否则先找到做子树中最大的元素ptemp, 用它交换p, 然后ptemp由ptemp的左孩子代替(因为它一定没有右孩子)bst_node* ptemp = p->left;bst_node* qtemp = NULL;while(ptemp->right != NULL) {qtemp = ptemp;ptemp = ptemp->right;}q->right = ptemp;qtemp->right = ptemp->left;ptemp->left = p->left;ptemp->right = p->right;Free(p);}
}

本系列教程由 西风逍遥游 原创，转载请注明出处：http://blog.csdn.net/xfxyy_sxfancy

这篇关于西风的数据结构教程（3）——二叉树的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---