数据结构---字典树（Tire）

本文主要是介绍数据结构---字典树（Tire），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

字典树是一种能够快速插入和查询字符串的多叉树结构，节点的编号各不相同，根节点编号为0

Trie树，即字典树，又称单词查找树或键树，是一种树形结构，是一种哈希树的变种。

核心思想也是通过空间来换取时间上的效率

在一定情况下字典树的效率要比哈希表要高

字典树在解决公共前缀的使用，所以叫前缀树

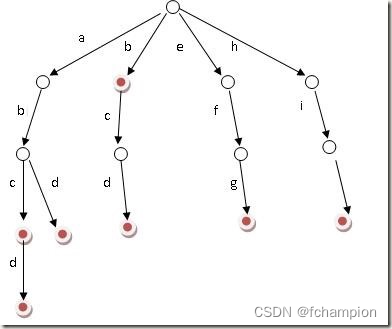
 先说如何创建字典树

这个是只有26个小写字母存放的字典树

class TrieNode{
public:TrieNode* next[26];bool isword;TrieNode(){memset(next,NULL,sizeof(next));isword=false;}~TrieNode(){for(int i=0;i<26;i++)if(next[i])delete next[i];}
};

也可以直接用c++中的特殊的数据结构来实现

struct Node {unordered_map<int, Node*> son;int cnt = 0;
};

但是在下面必须要对根节点进行补充，根节点为空

Node *root = new Node();

leetcode3043. 最长公共前缀的长度-CSDN博客

leetcode3042. 统计前后缀下标对 I-CSDN博客

力扣（LeetCode）官网 - 全球极客挚爱的技术成长平台

这道题之前用的暴力去模拟这个过程,效率太低,，采用前缀树来解决

class Solution {
public:long long countPrefixSuffixPairs(vector<string>& words) {long long cnt=0;int i,j;for(i=0;i<words.size()-1;i++){for(j=i+1;j<words.size();j++){if(words[j].find(words[i])==0 && words[j].rfind(words[i])==words[j].length()-words[i].length()){cnt++;}}}return cnt;}
};

但是前缀树解决的是前缀的问题，这道题让解决的是前缀和后缀的问题，所以想要把这个字符串转变一下来解决，

【1】首先我先到的是建造两个前缀树，一个正向前缀树，一个反向前缀树

 【2】可以用一个pair去储存步骤1的过程

正 ab                   abcdab

反 ba                   badcba

[(a,b),(b,a)]             [(a,b),(b,a),.....]

由此可见如果是前后缀的话，应该会在pair列表中出现

class Node:__slots__ = 'son', 'cnt'def __init__(self):self.son = dict()self.cnt = 0class Solution:def countPrefixSuffixPairs(self, words: List[str]) -> int:ans = 0root = Node()for t in words:z = self.calc_z(t)cur = rootfor i, c in enumerate(t):if c not in cur.son:cur.son[c] = Node()cur = cur.son[c]if z[-1 - i] == i + 1:  # t[-1-i:] == t[:i+1]ans += cur.cntcur.cnt += 1return ansdef calc_z(self, s: str) -> List[int]:n = len(s)z = [0] * nl, r = 0, 0for i in range(1, n):if i <= r:z[i] = min(z[i - l], r - i + 1)while i + z[i] < n and s[z[i]] == s[i + z[i]]:l, r = i, i + z[i]z[i] += 1z[0] = nreturn z

这篇关于数据结构---字典树（Tire）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---