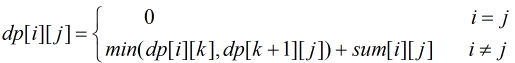本文主要是介绍sdnu 1045.石子合并1 1048.石子合并2,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
原题链接:
1045: http://210.44.14.31/problem/show/1045
1048: http://210.44.14.31/problem/show/1048
1045:有n堆石子排成一行,每次选择相邻的两堆石子,将其合并为一堆,记录该次合并的得分为两堆石子个数之和。已知每堆石子的石子个数,求当所有石子合并为一堆时,最小的总得分。
设dp[i][j]表示第i到第j堆石子合并的最优值。
那么就有状态转移公式:
代码如下:
#include<iostream>
#include<cstdio>
using namespace std;const int MAX_INT = 1 << 30;
int stone[200 + 5];
int dp[200 + 2][200 + 2];
int sum[200 + 5]; //存1到n堆的石子总数目
int n;int min(int x, int y)
{return x > y ? y : x;
}void GetMin()
{for (int len = 1; len <= n; len++){for (int begin = 1; begin + len <= n; begin++){int end = begin + len;int temp = sum[end] - sum[begin - 1]; //存begin到end堆石子的总数目,也可直接放入min函数中dp[begin][end] = MAX_INT;for (int k = begin; k < end; k++)dp[begin][end] = min(dp[begin][end], dp[begin][k] + dp[k + 1][end] + temp); //更新dp[begin][end]的值}}return ;
}int main()
{scanf_s("%d", &n);sum[0] = 0;for (int i = 1; i <= n; i++){scanf_s("%d", &stone[i]);sum[i] += stone[i] + sum[i - 1];}GetMin();printf("%d\n",dp[1][n]);return 0;
}1048:有n堆石子排成一圈,每次选择相邻的两堆石子,将其合并为一堆,记录该次合并的得分为两堆石子个数之和。已知每堆石子的石子个数,求当所有石子合并为一堆时,最小的总得分。
状态转移方程同上,只需解决一下边界问题。
代码如下:
#include<cstdio>
using namespace std;const int MAX_INT = 1 << 30;
int dp[200 + 2][200 + 2];
int sum[200 + 5];
int stone[200 + 5];
int n,MIN;int GetSum(int begin, int end)
{if (end <= n)return sum[end] - sum[begin - 1];return sum[n] - sum[begin - 1] + sum[end%n];}
int min(int x, int y)
{return x > y ? y : x;
}void GetMin()
{for (int len = 1; len <= n; len++){for (int begin = 0; begin <= n; begin++){int end = (begin + len) % n == 0 ? n : (begin + len) % n;int temp = GetSum(begin, begin+len); //注意传begin+lendp[begin][end] = MAX_INT;for (int k = 0; k < len; k++)dp[begin][end] = min(dp[begin][end], dp[begin][(begin + k) % n == 0 ? n : (begin + k) % n] + dp[(begin + k + 1) % n == 0 ? n : (begin + k + 1) % n][end] + temp);//dp[][0]不使用}}MIN = dp[1][n];for (int i = 2; i <= n;i++)if (MIN > dp[i][i - 1])MIN = dp[i][i - 1];
}int main()
{scanf_s("%d", &n);sum[0] = 0;for (int i = 1; i <= n; i++){scanf_s("%d", &stone[i]);sum[i] += sum[i - 1] + stone[i];}GetMin();printf("%d\n", MIN);return 0;
}
这篇关于sdnu 1045.石子合并1 1048.石子合并2的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!