力扣日记2.20-【回溯算法篇】491. 非递减子序列

本文主要是介绍力扣日记2.20-【回溯算法篇】491. 非递减子序列，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

力扣日记：【回溯算法篇】491. 非递减子序列

日期：2023.2.20
参考：代码随想录、力扣
ps：放了个寒假，日记又搁置了三星期……（下跪忏悔）

491. 非递减子序列

题目描述

难度：中等

给你一个整数数组 nums ，找出并返回所有该数组中不同的递增子序列，递增子序列中至少有两个元素。你可以按任意顺序返回答案。

数组中可能含有重复元素，如出现两个整数相等，也可以视作递增序列的一种特殊情况。

示例 1：

输入：nums = [4,6,7,7]
输出：[[4,6],[4,6,7],[4,6,7,7],[4,7],[4,7,7],[6,7],[6,7,7],[7,7]]

示例 2：

输入：nums = [4,4,3,2,1]
输出：[[4,4]]

提示：

1 <= nums.length <= 15
-100 <= nums[i] <= 100

题解

cpp ver

class Solution {
public:vector<int> path;vector<vector<int>> result;vector<vector<int>> findSubsequences(vector<int>& nums) {// nums.size >= 2if (nums.size() < 2)    return result;backtracking(nums, 0, -200);    // -100 <= nums[i] <= 100return result;}void backtracking(vector<int>& nums, int startindex, int lastnum) {// 子序列至少有两个值if (path.size() >= 2)   result.push_back(path);int used[201] = {0}; // 这里使用数组来进行去重操作，题目说数值范围[-100, 100]，在for循环前重置，每个for循环对应一个// for 循环for (int i = startindex; i < nums.size(); i++) {// // 树层去重(如果本次取出元素与上一个元素一样，则跳过该元素)// if (i > startindex && nums[i] == nums[i - 1]) continue;// 注意，本题由于不能对元素进行排序，所以树层中也可能出现不连续元素重复的可能，所以不能简单的用相邻元素重复来去重// 可以用哈希表来去重(或数组)if (used[nums[i] + 100] != 0) continue; // 如果是已经取过的元素，则跳过该元素used[nums[i] + 100] = 1;	// 记录该元素// 如果本次取出元素比上一次取的元素低，则不进入递归，但不结束for循环// (注意取值可不连续!!!如[4,7,6,7]中[4,7,7]也是递增子序列，所以这里不能break)if (nums[i] < lastnum)  continue;// 处理节点path.push_back(nums[i]);backtracking(nums, i + 1, nums[i]);path.pop_back();}}
};

复杂度

时间复杂度: O(n * 2^n)
空间复杂度: O(n)

思路总结

本题首先要明确“递增子序列”的概念
- 子序列问题本质上是子集问题
- 递增子序列（或者说非递减子序列）是可以从原集合中非连续取值的！！！
  - 这点是易错点，且单从题目描述或例子中不能得出此结论（但经过测试用例确实如此）
  - 以[4,7,6,7]为例子，[4,7,7]或[7,7]也是其子序列（这是不同于只能连续取值的字符串子串的）
所以本题在去重时，不能像 90.子集 II 那样通过相邻元素相同来去重（那种去重思路仅适用于能先对原集合进行排序的情况，但本题提前排序会改变原集合的非递增性质故不能提前排序），因为可能会在不连续的地方出现重复的元素。
- 可以通过哈希表的方法来去重（如用哈希set或效率更高的数组），如代码所示
  - 每层for循环都对应一个数组来记录某元素是否已经取过，如果已经取过，则跳过该元素，即：
```
	int used[201] = {0}; // 这里使用数组来进行去重操作，题目说数值范围[-100, 100]，在for循环前重置，每个for循环对应一个// for 循环for (int i = startindex; i < nums.size(); i++) {//用哈希表来去重(或数组)if (used[nums[i] + 100] != 0) continue; // 如果是已经取过的元素，则跳过该元素used[nums[i] + 100] = 1;	// 记录该元素...
```
对于需要为“递增子序列”的判断，实际上也是能否进行取值和递归（即所谓处理节点）的前提条件，即只有当前值不小于上一次取的值，才能进行取值和递归：
- 首先用last_num作为参数来记录上一次取的值，即在递归时令last_num = nums[i]，并且在满足上面的去重条件后，通过if (nums[i] < lastnum) continue;来过滤不满足递增条件的元素。
- 这里也可以不用last_num作为递归参数，而是用if (!path.empty() && nums[i] < path.back()) continue来表示，因为path.back()即为上一个取的值（前提是path不为空）
- 同时注意不能用break而要用contnue，理由是子序列的取值可以不连续，即使当前值不满足递增，其后面的元素也可能满足，因此不能直接break！！！
树形结构示意图
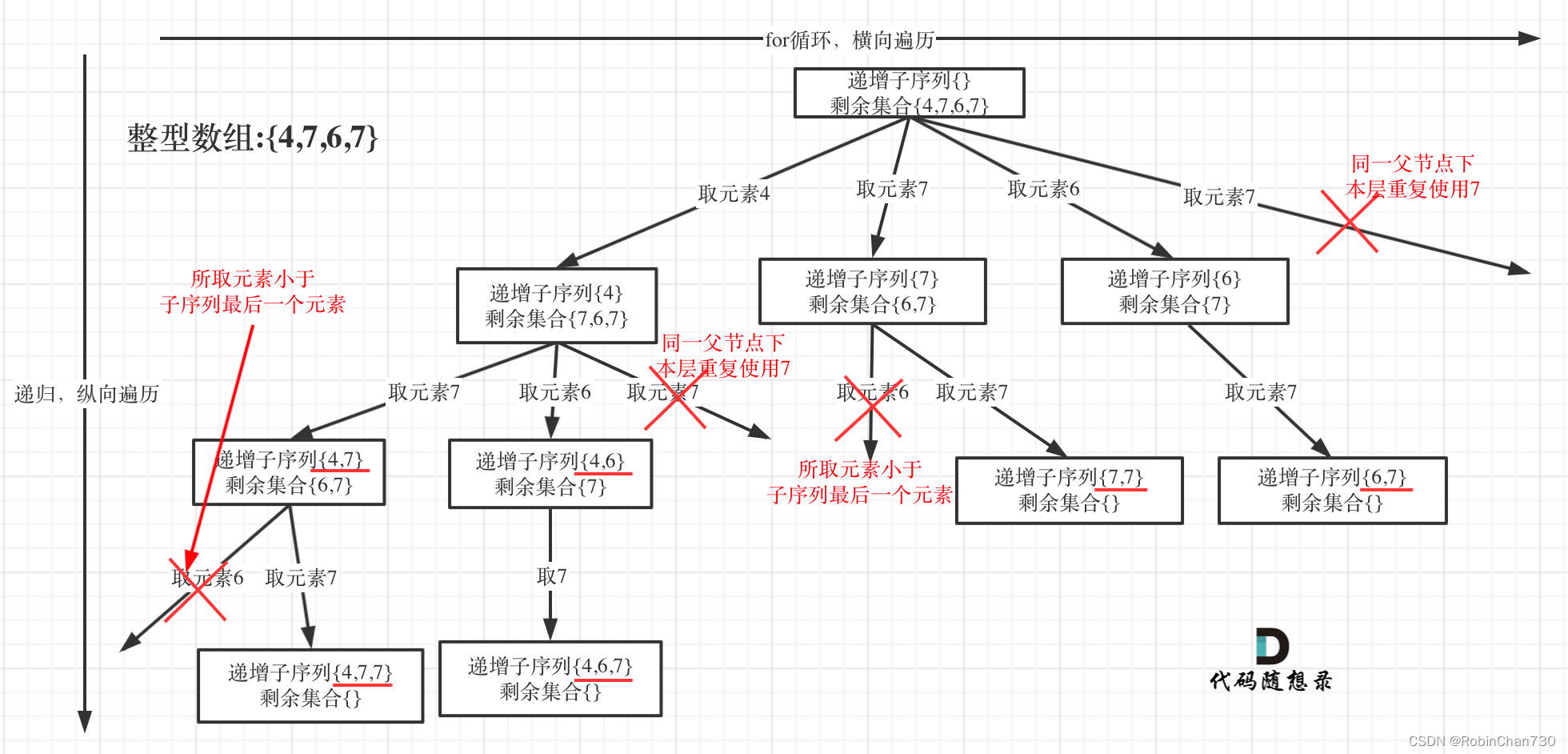
- 可见其中存在两种不符合条件的情况，一是“同一父节点下本层重复使用”，对应去重；二是“所取元素小于子序列最后一个元素”，对应“递增”条件。
三部曲：
- 返回值及传递参数：参数为经典的原数组nums以及startindex记录for循环取值的起始位置，除此之外，还用一个last_num记录递归纵向遍历中的上一个取值 （如果直接用path.back()表示则不需要此参数）
- 终止条件：对于子集问题，由于需要遍历各个节点进行存储，所以不需要专门的终止条件。这里注意子序列至少包含两个值，即path需要满足size>=2
  - 注：在原先的代码实现中，本来是在终止条件处实现递增条件的判断（即当出现小于上一个取值的元素，则终止），但是这样会使得最后一个path的存储非常麻烦，所以作废，还是需要将此递增条件的判断作为for循环中、处理节点（即取值并递归）的前提条件。
- for循环处理：
  - 去重（哈希表记录重复元素，重复则跳过）
  - 递增条件（小于上一个取值则跳过）
  - 处理节点（取值、递归、回溯）