第三十六天| 435. 无重叠区间、763.划分字母区间、56. 合并区间

本文主要是介绍第三十六天| 435. 无重叠区间、763.划分字母区间、56. 合并区间，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

Leetcode 435. 无重叠区间

题目链接：435 无重叠区间

题干：给定一个区间的集合 intervals ，其中 intervals[i] = [starti, endi] 。返回 需要移除区间的最小数量，使剩余区间互不重叠 。

思考：贪心法。和452 用最少数量的箭引爆气球原理类似。按照左边界排序，从左向右记录多余交叉区间的个数。或者按照右边界排序，从左向右记录非交叉区间的个数。最后用区间总数减去非交叉区间的个数就是需要移除的区间的个数。

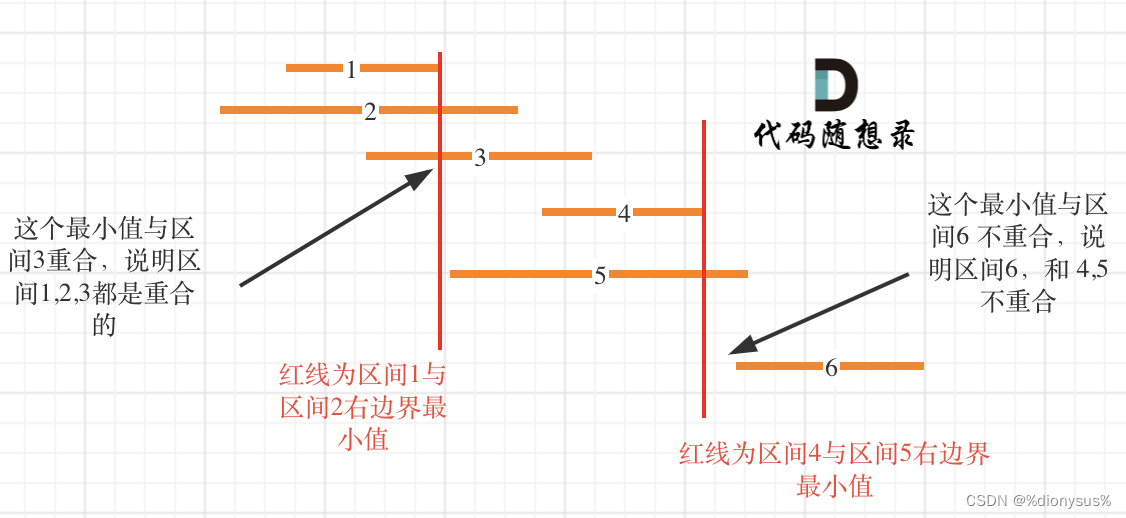
此图先按右边界排序，之后记录非交叉区间的个数还是有技巧的。取区间1 和区间2 右边界的最小值，因为这个最小值之前的部分一定是区间1 和区间2 的重合部分，如果这个最小值也触达到区间3，那么说明区间 1，2，3都是重合的。

代码一（按右边界排序）：

class Solution {
public:static bool cmp(const vector<int>& a, const vector<int>& b) {return a[1] < b[1];     //按右边界排序}int eraseOverlapIntervals(vector<vector<int>>& intervals) {if (intervals.size() == 0)  return 0;sort(intervals.begin(), intervals.end(), cmp);      //排序int count = 1;     //记录非重叠区间个数int end = intervals[0][1];      //记录当前重叠区间右边界for (int i = 1; i < intervals.size(); i++) {if (intervals[i][0] >= intervals[i - 1][1])count++;elseintervals[i][1] = min(intervals[i][1], intervals[i - 1][1]);        //更新重叠区间右边界}return intervals.size() - count;}
};

代码二（按左边界排序）：

class Solution {
public:static bool cmp(const vector<int>& a, const vector<int>& b) {return a[0] < b[0];     //按左边界排序}int eraseOverlapIntervals(vector<vector<int>>& intervals) {if (intervals.size() == 0)  return 0;sort(intervals.begin(), intervals.end(), cmp);      //排序int result = 0;     //记录多余重叠区间个数for (int i = 1; i < intervals.size(); i++) {if (intervals[i][0] < intervals[i - 1][1]) {        //存在重叠区间intervals[i][1] = min(intervals[i][1], intervals[i - 1][1]);        //更新重叠区间右边界result++;}}return result;}
};

Leetcode 763.划分字母区间

题目链接：763 划分字母区间

题干：给你一个字符串 s 。我们要把这个字符串划分为尽可能多的片段，同一字母最多出现在一个片段中。

注意，划分结果需要满足：将所有划分结果按顺序连接，得到的字符串仍然是 s 。

返回一个表示每个字符串片段的长度的列表。

1 <= s.length <= 500
s 仅由小写英文字母组成

思考：贪心法。先寻找所有字母的最后出现的下标位置，和其首次出现的位置形成区间。接下来将重叠的区间合并起来，并记录每个不重叠区间的大小。由于按顺序遍历字符串因此在合并区间时只需要更新右边界，在不重叠时初始化新区间的边界。

代码：

class Solution {
public:vector<int> partitionLabels(string s) {int lastPresence[27] = { 0 };       //记录所有字母最后出现的下标位置for (int i = 0; i < s.size(); i++)      lastPresence[s[i] - 'a'] = i;int left = 0;       //记录区间的左边界int right = 0;      //记录区间的右边界vector<int> result;for (int i = 0; i < s.size(); i++) {right = max(right, lastPresence[s[i] - 'a']);       //更新当前区间右边界if (i == right) {result.push_back(right - left + 1);left = i + 1;       //新区间左边界}}return result;}
};

Leetcode 56. 合并区间

题目链接：56 合并区间

题干：以数组 intervals 表示若干个区间的集合，其中单个区间为 intervals[i] = [starti, endi] 。请你合并所有重叠的区间，并返回 一个不重叠的区间数组，该数组需恰好覆盖输入中的所有区间 。

思考：贪心法。本题和435. 无重叠区间非常相似，都是先排序后再处理。区别：处理过程中如果记录区间和当前处理区间存在重叠，则更新记录区间的右边界，否则记录当前处理区间。

代码：

class Solution {
public:static bool cmp(const vector<int>& a, const vector<int>& b) {return a[0] < b[0];     //按左区间排序}vector<vector<int>> merge(vector<vector<int>>& intervals) {vector<vector<int>> result;if (intervals.size() == 0)  return result;sort(intervals.begin(), intervals.end(), cmp);result.push_back(intervals[0]);     //将首个区间放入结果集，后面出现重叠则修改右边界for (int i = 1; i < intervals.size(); i++) {if (result.back()[1] >= intervals[i][0])result.back()[1] = max(result.back()[1], intervals[i][1]);      //更新重叠区间右边界elseresult.push_back(intervals[i]);     //区间不重叠则加入新区间}return result;}
};

自我总结：