本文主要是介绍Codeforces Round 925 (Div. 3)G. One-Dimensional Puzzle 组合数,隔板法,允许有空的先欠做法,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
Problem - G - Codeforces
当然得先分析题目的情况
类型1,2的数量差不能大于1:
样例3失败解释:
4 6 100 200
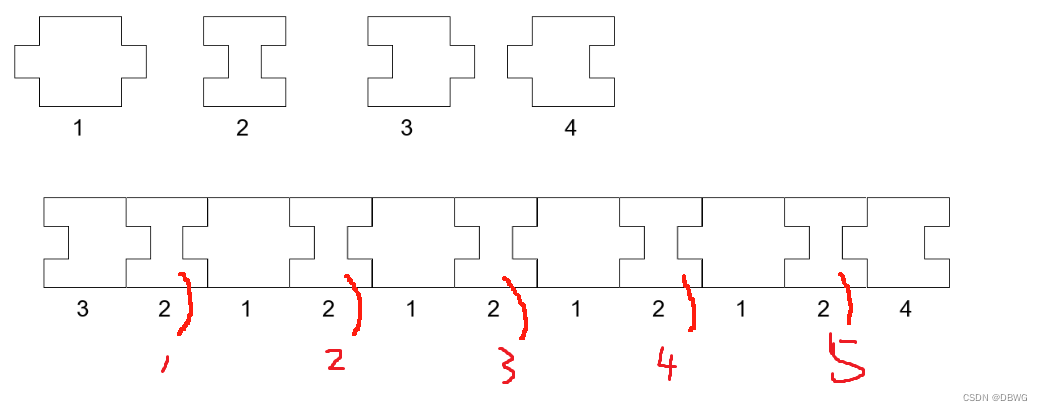
第六个型号2是没法再放进去的,所以可以分析出 类型1与类型2之间的差不能超过1
类型3,4可以自己拼自己;
3可以在1 2间,4 在2 1间:
1 2可以拼在一起,也可以在1 2 之间插入若干个3。
4同理。
所以题目问有多少种情况。
当1,2数目不同时:
// 1 2 1
//4 3 4 3
// 2 1 2
//3 4 3 4
(设a,b,c,d分别是1,2,3,4类型的数目)
可以看出对3和4来说可以插入的位置数目是相同的,为max(a,b)
那么问题等价于若干个盒子,我们把一对球放入盒子中,有多少种放法。(3和4的方法互补干扰,放法之积即为答案。)
而且1 2 之间可以为空,“隔板法”去放3是不行的(隔板法把n个分成若干份,每份至少为1个)。
比如c个球放入a个盒子,这里我们可以先欠做法:
先欠做法:
我们放c+a个球,最后每个盒子取1个,不就把这a个取出来了吗。
这种就等价于c个球放入a个盒子,允许有空了
当1,2数目相同时:
// 1 2 1 2
//4 3 4 3 4
// 2 1 2 1
//3 4 3 4 3
要么3多一个,要么4多一个,两种情况加起来即可,同上做法。
代码:
注意阶乘要开到2e6,因为c虽然最大为1e6,但是我们先欠做法计算的是c + gap
ll a[2000005];
ll ksm(int x, int y, int mod) {if (x == 1) return 1;ll res = 1, base = x;while (y) {if (y & 1) res = (res * base) % mod;base = (base * base) % mod;y >>= 1;}return res;
}ll C(ll n, ll m, ll p)
{if (m > n)return 0;return ((a[n] * ksm(a[m], p - 2, p)) % p * ksm(a[n - m], p - 2, p) % p);
}void solve()
{int a, b, c, d;cin >> a >> b >> c >> d;if (abs(a - b) > 1 || a == 0 && b == 0 && c!=0&& d!=0){cout << 0 << endl;return;}if (a == 0&&b==0){if (c == 0 || b == 0)cout << 1 << endl;elsecout << 0 << endl;return;}//int ans = 0;int gap = max(a, b);if (a == b){ans = (C(c + gap, gap, mod) * C(d + gap - 1, gap - 1, mod) % mod + C(c + gap - 1, gap - 1, mod) * C(d + gap, gap, mod) % mod)%mod;}else{ans = C(c + gap - 1, gap-1, mod) * C(d + gap - 1, gap-1, mod) % mod;}cout << ans << endl;
}
signed main()
{ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);a[0] = a[1] = 1;for (int i = 2; i <= 2000000; i++){a[i] = a[i - 1] * i%mod;}int t = 1;cin >> t;while (t--){solve();}return 0;
}这篇关于Codeforces Round 925 (Div. 3)G. One-Dimensional Puzzle 组合数,隔板法,允许有空的先欠做法的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




