灰色预测GM(1,1)模型及MATLAB实现

因为做毕设开始接触的灰色预测，发表的第一篇小论文也是基于GM(1,1)灰色预测模型的，这一篇主要想详细记录一下灰色理论的基础知识以及分享一下我在毕设中用到的MATLAB代码。如有问题欢迎指正交流(#^.#)

灰色预测方法是一种用来对灰色系统进行预测的方法，灰色系统是指信息不完全的一种系统，是一种广泛用于研究少数据、贫信息问题的方法。GM(1,1)预测模型的基本原理是：对某一数据序列使用累加的方法生成一组变化趋势明显的新序列，对新的数据序列建立模型并进行预测，然后利用累减的方法逆向计算，使其恢复为原始序列，以此得出预测模型结果。
GM(1,1)建模过程如下：
设一组原始数列为：

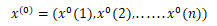
n为数据个数，对x（0）进行一阶累加生成数列：

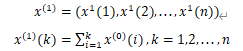
生成x（1）的紧邻均值数列：

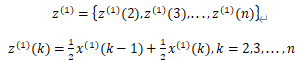
根据灰色系统理论对x（1）建立关于t的白化微分方程GM(1,1)：

其中，a是发展系数，b是灰作用量，z（1）（k）是白化背景值，x（0）（k）是灰导数，且

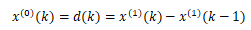
带入n值可得

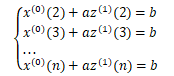
引入矩阵向量记号：

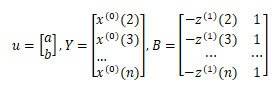
于是GM（1,1）模型可表示为：

利用最小二乘法可求得a，b的值

对于GM(1,1)的灰微分方程，如果将时刻k=2,3,…,n视为连续变量t，则之前的x(1)视为时间t函数，于是得到GM(1,1)灰微分方程对应的白化微分方程：

解得：

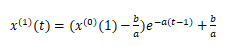
于是得到预测值：

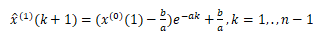
从而可以得到还原预测值：

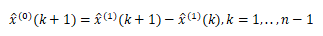
为确保GM(1,1)建模的实用性，需在预测前对已有的数据进行验证。计算数列的级比：

当计算出来的级比均落在可覆盖区间内时，则可以对数列x（0）建立GM（1,1）模型，并进行灰色预测。可覆盖区间X：

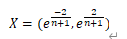
模型的误差检验
对建立的灰色模型进行精度检验方法如下，且预测精度等级对照表如表1所示。
均值：

方差：

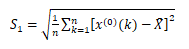
残差的均值：

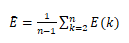
残差的方差：

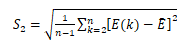
后验差比值C：

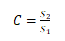
小误差概率P：


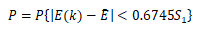
MATLAB代码实现：

%建立符号变量a(发展系数)和b(灰作用量)
syms a b;
c = [a b]';%原始数列 A
A=input('请输入原始序列(格式为[1.5, 2.1, 3.3, 4.6, 5.7]): ');
m=input('请输入后续需要预测的数据个数: ');
n = length(A);%对原始数列 A 做累加得到数列 B
B = cumsum(A);%对数列 B 做紧邻均值生成
for i = 2:nC(i) = (B(i) + B(i - 1))/2; 
end
C(1) = [];%构造数据矩阵 
B = [-C;ones(1,n-1)];
Y = A; Y(1) = []; Y = Y';%使用最小二乘法计算参数 a(发展系数)和b(灰作用量)
c = inv(B*B')*B*Y;
c = c';
a = c(1); b = c(2);%预测后续数据
F = []; F(1) = A(1);
for i = 2:(n+m)F(i) = (A(1)-b/a)/exp(a*(i-1))+ b/a;
end%对数列 F 累减还原,得到预测出的数据
G = []; G(1) = A(1);
for i = 2:(n+m)G(i) = F(i) - F(i-1); %得到预测出来的数据
enddisp('预测数据为：');
G%模型检验H = G(1:10);
%计算残差序列
epsilon = A - H;%方差比C检验
C = std(epsilon, 1)/std(A, 1)
if C<0.35disp('系统预测精度好')else if C<0.5disp('系统预测精度合格')else if C<0.65disp('系统预测精度勉强')elsedisp('系统预测精度不合格')endend
end%绘制曲线图
t1 = 0:9;
t2 = 0:(9+m);plot(t1, A,'bo--'); hold on;
plot(t2, G, 'r*-');
xlabel('距瓦斯涌出点距离'); ylabel('瓦斯浓度');
legend('实测瓦斯浓度','预测瓦斯浓度');
title('瓦斯浓度变化曲线');
grid on;

上述程序为当时做毕设时根据我的任务目标来编写的，原始数据个数为10，后续预测数据个数输入为10后得到拟合及预测结果图如下：

根据上述结果分析可得，GM（1,1）模型在本次实验中平均模拟相对误差为2.176%，预测精度良好。