[经典面试题][百度]数轴上从左到右有n各点a[0], a[1], ……,a[n -1]，给定一根长度为L的绳子，求绳子最多能覆盖其中的几个点。

本文主要是介绍[经典面试题][百度]数轴上从左到右有n各点a[0], a[1], ……,a[n -1]，给定一根长度为L的绳子，求绳子最多能覆盖其中的几个点。，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

题目

数轴上从左到右有n各点a[0], a[1], ……,a[n -1]，给定一根长度为L的绳子，求绳子最多能覆盖其中的几个点。

思路一

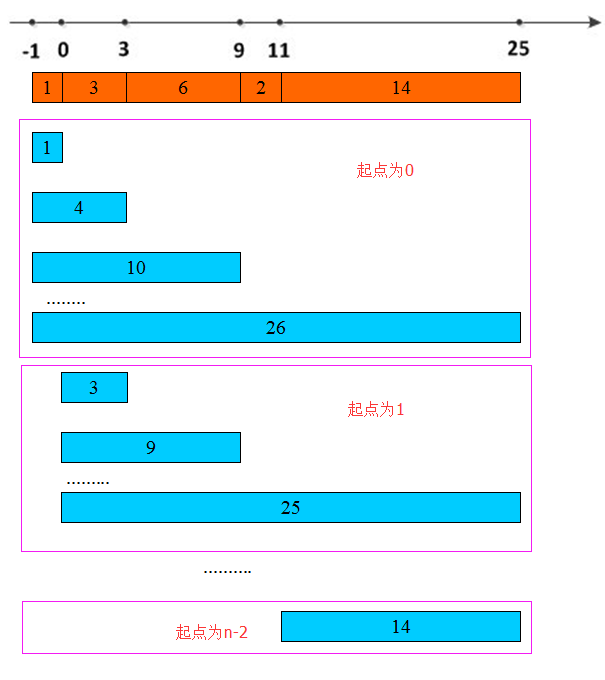
遍历所有区间跟绳子L比较。
i遍历区间起点，j遍历区间终点。
时间复杂度为O(n^2)

代码一

    /*-------------------------------------*   日期：2015-02-08*   作者：SJF0115*   题目: 绳子覆盖*   来源：百度2014*   博客：------------------------------------*/#include <iostream>#include <vector>#include <cstring>#include <algorithm>using namespace std;class Solution {public:// points 给定点 L 绳子长度int RopeCover(vector<int> points,int L) {int size = points.size();if(size <= 0){return 0;}//if// 所能覆盖的最多点数int max = 0;int start = 0,end = 0;// i起点 j终点 遍历所有区间;for(int i = 0;i < size-1;++i){for(int j = i+1;j < size;++j){if(points[j] - points[i] <= L && j - i + 1 > max){max = j - i + 1;start = i;end = j;}//if}}//forcout<<"起点->"<<start<<" 终点->"<<end<<endl;return max;}};int main(){Solution s;vector<int> points = {-1,0,3,9,11,25};int L = 15;int result = s.RopeCover(points,L);// 输出cout<<result<<endl;return 0;}

思路二

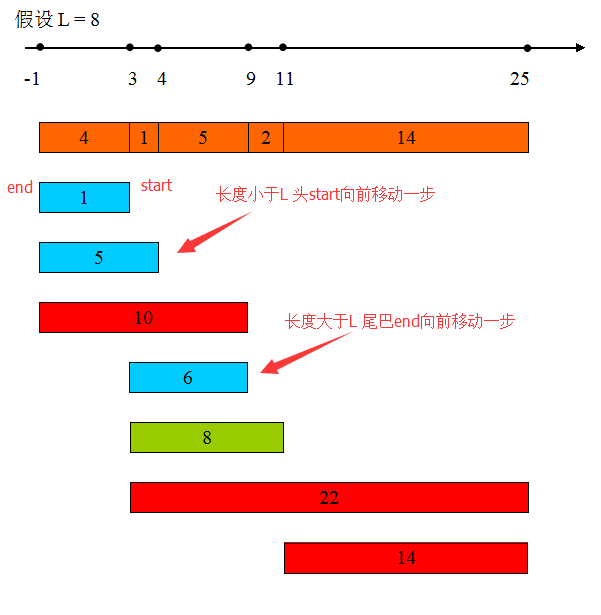
两个指针,start，end。
如果points[front]-points[rear]<=L，头start向前移动一步。
如果points[front]-points[rear]>L，尾巴end向前移动一步。
每个数最多遍历2遍，因此时间复杂度为O(n)。
对于这个算法，某网友给了一个形象的比喻：
就好像一条长度为L的蛇。头伸不过去的话，就把尾巴缩过来最多只需要走一次，就知道能覆盖几个点

代码二

    /*-------------------------------------*   日期：2015-02-08*   作者：SJF0115*   题目: 绳子覆盖*   来源：百度2014*   博客：------------------------------------*/#include <iostream>#include <vector>#include <cstring>#include <algorithm>using namespace std;class Solution {public:// points 给定点 L 绳子长度int RopeCover(vector<int> points,int L) {int size = points.size();if(size <= 0){return 0;}//if// 所能覆盖的最多点数int max = 0;int start = 1,end = 0;int maxS = 0,maxE = 0;while(end < start){if(points[start] - points[end] <= L){if(start - end + 1 > max){max = start - end + 1;maxS = end;maxE = start;}//if// 头向前移动一格++start;}//ifelse{// 尾巴向前移动一格++end;}}//whilecout<<"起点->"<<maxS<<" 终点->"<<maxE<<endl;return max;}};int main(){Solution s;vector<int> points = {-1,3,4,9,11,25};int L = 8;int result = s.RopeCover(points,L);// 输出cout<<result<<endl;return 0;}

如果本方法有什么问题，欢迎指正。如果有更好的方法，欢迎指导。

这篇关于[经典面试题][百度]数轴上从左到右有n各点a[0], a[1], ……,a[n -1]，给定一根长度为L的绳子，求绳子最多能覆盖其中的几个点。的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---