堆排序Heap Sort——浅显易懂+Java实现

本文主要是介绍堆排序Heap Sort——浅显易懂+Java实现，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

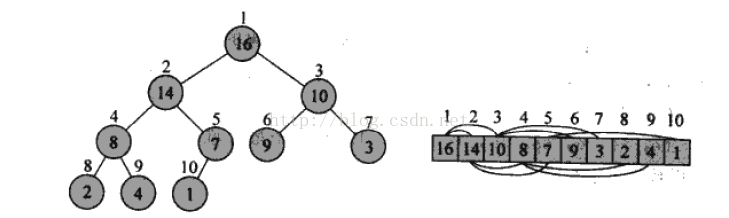
最近在恶补一些计算机基础内容，看到了堆排序，想想以前常说堆栈堆栈，但我竟然连堆有哪些应用都记不得了，所以，重温了堆排序后，我来给大家分享一下，希望能对大家有所帮助。（代码实现不采用伪代码，使用java实现，毕竟来看博客的都不想和看书一样把）

       首先，堆是一种数据结构，你可以把他看成一颗完全二叉树，如下图所示：圆圈上方的数字代表下标：他的特性就是：父结点的值要大于两个儿子结点的值。

        上图选自算法导论，下标从1开始，但我们写的时候，肯定是要按照从0开始的下标来写代码拉，这一点后面不会再特别说明了。

        虽然堆可以用数组表示，但堆和数组有所区别，主要是在于数组的长度（length）不一定等于堆的大小（heapSize）。heapSize <= length。下标大于heapSize但小于length的值都不属于堆结构。

        所以，在java里先新建一个类来表示堆：没有使用数组的原因是，java里数组初始化以后就不能再添加元素了，在讲解后面内容的时候会有所不方便。

    public class Heap {  private ArrayList<Integer> A;  private int heapSize;  public ArrayList<Integer> getA() {  return A;  }  public void setA(ArrayList<Integer> a) {  A = a;  }  public int getHeapSize() {  return heapSize;  }  public void setHeapSize(int heapSize) {  this.heapSize = heapSize;  }  } 

很容易得知，结点i的左儿子右儿子或父结点的下标的计算函数

// 左节点下标public int left(int i) {return i * 2 + 1;}// 右节点下标public int right(int i) {return i * 2 + 2;}// 父节点下标public int parent(int i) {return (i - 1) / 2;}

要实现堆排序，我们首先得保持堆的性质。（下面用最大堆举例）

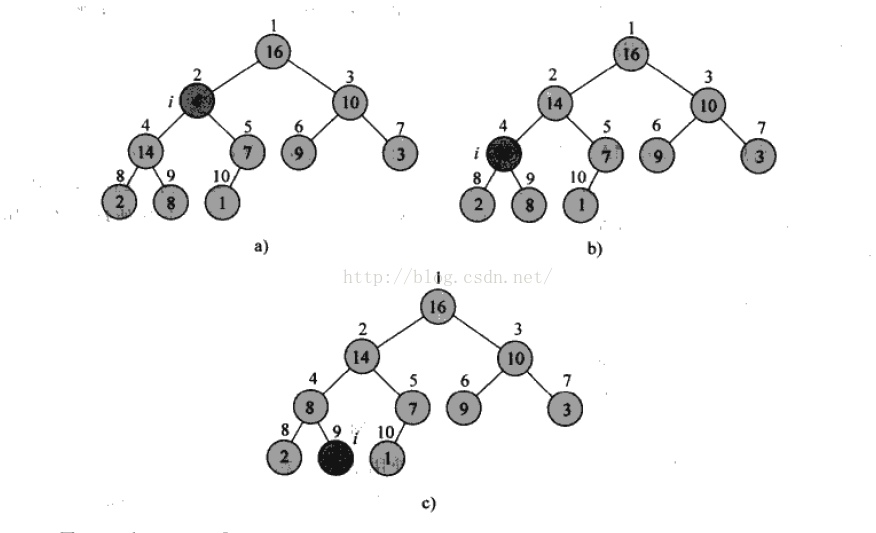
      当儿子结点大于父节点的时候，就失去了最大堆的性质，所以在这个时候，我们只要把儿子结点和父结点交换，但是交换以后，被交换的父结点的儿子结点发生了变化，可能会继续违背最大堆这个性质，所以要递归调用这个算法。过程大致如下图所示：

对2号结点进行最大堆性质的保持

        要实现这个过程的代码如下：

   /*** 递归实现的堆排序* @param heap 堆* @param i 当前坐标*/public void MaxHeapify(Heap heap, int i) {int l = left(i);int r = right(i);int largest = i;if (l < heap.getHeapSize() && heap.getA().get(l) > heap.getA().get(i)) {largest = l;}if (r < heap.getHeapSize() && heap.getA().get(r) > heap.getA().get(largest)) {largest = r;}if (largest != i) {int temp = heap.getA().get(i);heap.getA().set(i, heap.getA().get(largest));heap.getA().set(largest, temp);} elsereturn;MaxHeapify(heap, largest);}

其实，这个算法是可以非递归实现的，可以提升效率：

/*** 非递归实现的堆排序* @param heap 堆* @param i 当前坐标*/public void MaxHeapifyNoRecursive(Heap heap, int i) {while (true) {int l = left(i);int r = right(i);int heapSize = heap.getHeapSize();ArrayList<Integer> A = heap.getA();int largest = i;if (l < heapSize && A.get(l) > A.get(i)) {largest = l;}if (r < heapSize && A.get(r) > A.get(largest)) {largest = r;}if (largest != i) {int temp = A.get(i);A.set(i, A.get(largest));A.set(largest, temp);} elsereturn;i = largest;}}

有了上述的算法，我们就可以进行建堆操作了，建堆的过程很简单，从下标heapSize - 1开始，对每个结点都执行MaxHeapify就行了，但是叶子结点由于没有子结点，所以只需要从（heapSize - 1）/2开始，对每个结点都执行MaxHeapify就行了

/*** 构建最大堆* @param heap 堆*/public void BuildMaxHeap(Heap heap) {int heapsize = heap.getHeapSize();for (int i = (heapsize - 1) / 2; i>= 0; i--) {MaxHeapify(heap, i);}}

这个过程大概如下图所示：

接下来，就是堆排序算法了。

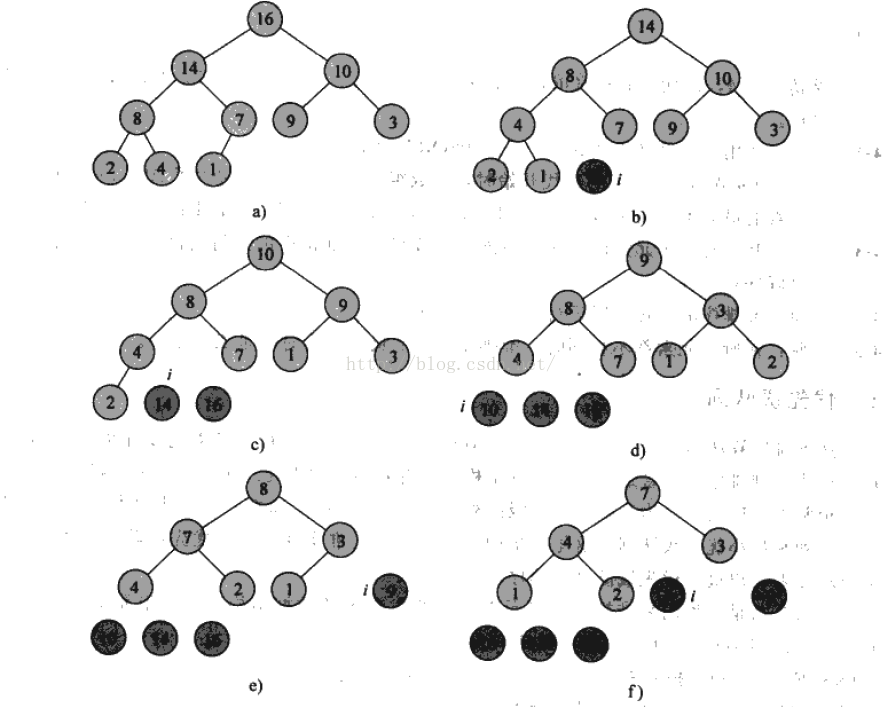
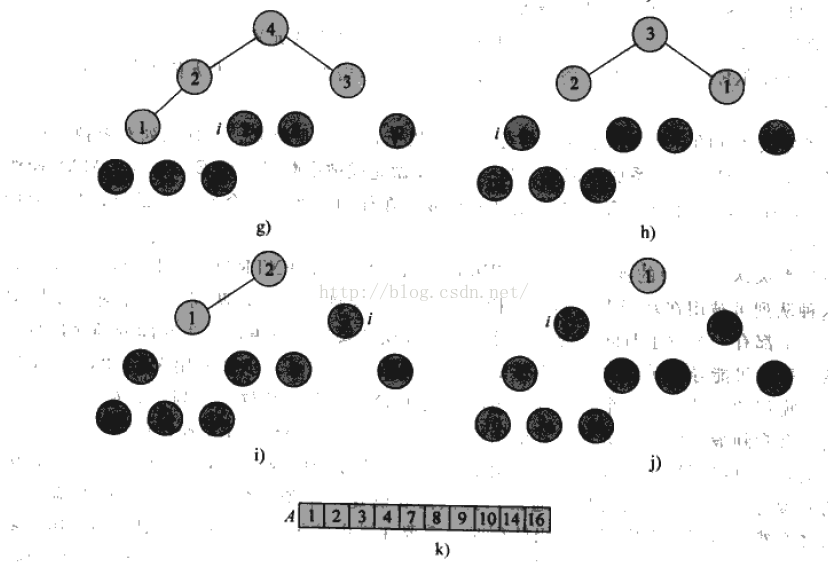
先用BuildMaxHeap把输入的数组A构造成最大堆。然后，把下标heapSize - 1的元素和下标为0的元素对换，通过减小heapSize，让下标为heapSize - 1的元素从堆中剔除，再调用MaxHeapify（heap, 0）即可保证最大堆的性质。重复这个过程，直到堆中只剩下一个元素。

/*** 堆排序算法* @param heap 堆*/public void HeapSort(Heap heap) {BuildMaxHeap(heap);int length = heap.getA().size(), heapSize = heap.getHeapSize();for (int i = length - 1; i > 0; i--) {int temp = heap.getA().get(i);heap.getA().set(i, heap.getA().get(0));heap.getA().set(0,temp);heap.setHeapSize(--heapSize);MaxHeapify(heap, 0);}}

这个过程的图示如下：

这样堆排序算法就算完成了，复杂度仅为O(nlg(n))，但是，其实快速排序往往优于它，虽然复杂度和它一样。

上面有所有方法的单元测试：https://github.com/qjkobe/IntroductionToAlgorithms

如果有啥问题记得跟我说哈

原文：http://blog.csdn.net/qj30212/article/details/52443250

我略微修改了一下代码和描述

这篇关于堆排序Heap Sort——浅显易懂+Java实现的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---