本文主要是介绍8.4 贪心策略例题---区间选点问题,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
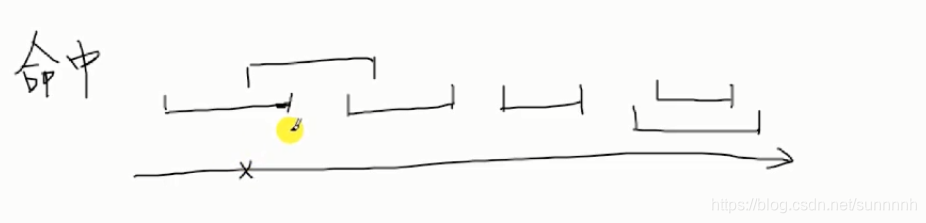
例题1:在区间内找尽可能少的点,能够命中所有区间
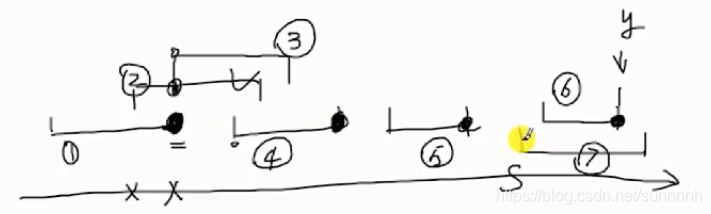
也是对开始和结束时间排序(结束时间从小到大排),每次选取结束时间点作为一个点,命中的区间数最大
如果选取一个区间的终点,命中了多个区间,接着再从未命中区间的终点开始选取点
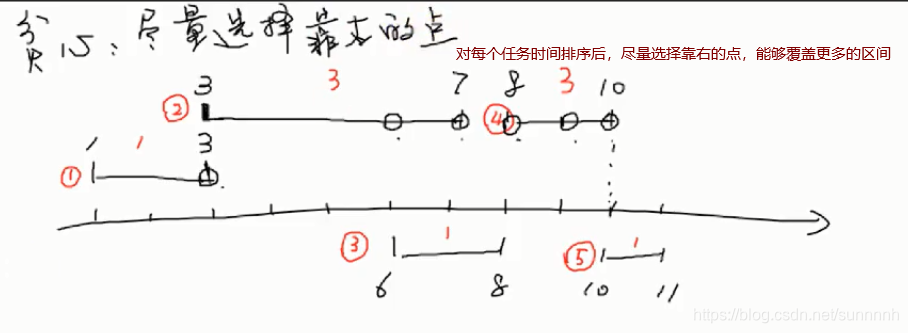
例题2(在上题基础上的提高):要求每个区间有多个点
输入:
n(表示n个区间)
接下来n行输入 (每行三个数)
每个区间的开始时间 结束时间 含有点的个数
输出:
最少需要多少点
例如
输入:

输出:
![]()

import java.util.Arrays;
import java.util.Scanner;public class Main {/**思路:(1)首先将每个任务的开始时间、结束时间、需要包含的点封装在对象中,并按照结束时间递增排序(结束时间相同,按照开始时间递增排序)* (2)依次遍历每一个区间* 查找该区间已存在的点* 如果已存在的点==其需要的点,则继续遍历下一个区间* 如果已存在的点<其需要的点,则从右向左为其分配点,并更新其所需的点,直到其所需的点为0*关键:判断某个点是否已存在:建立一个数组axs作为数轴,其范围1~所有任务中最晚的结束时间,如果位置i已经设点,将axs[i]=1*测试数据:
5
3 7 3
8 10 3
6 8 1
1 3 1
10 11 1*/public static void main(String[] args) {//(1)输入相关数据Scanner sc = new Scanner(System.in);int n = sc.nextInt();int[][] a = new int[n][3];for(int i=0;i<n;i++) {a[i][0] = sc.nextInt();//开始时间a[i][1] = sc.nextInt();//结束时间a[i][2] = sc.nextInt();//需要的点数}//(2)将每个区间开始、结束时间、需要的点数封装起来,并排序Task[] task = new Task[n];for(int i=0;i<n;i++) {task[i] = new Task(a[i][0],a[i][1],a[i][2]);}//排序Arrays.sort(task);//(3)设置一个数组axs作为数轴,记录被占用的点。1表示被占用int max = task[n-1].e;//最后一个任务的结束时间是数轴中最大的点int[] axs = new int[max+1];//下标0~max//(4)依次遍历每个任务,为其加点for(int i=0;i<n;i++) {int start=task[i].s;int end=task[i].e;int sum = getSumPoint(start,end,axs);//获取当前区间已存在的点数while(sum<task[i].c) {//点数不足,继续从右向左加点.注意:是while循环if(axs[end]==0) {//最右端没有加点axs[end]=1;end--;sum++;}else {end--;}}}System.out.println(getSumPoint(1, max, axs));}//获取区间s~e中已存在的点数
private static int getSumPoint(int s, int e, int[] axs) {int cnt=0;for(int i=s;i<=e;i++) {cnt+=axs[i];}return cnt;
}}
class Task implements Comparable<Task>{int s;//开始时间int e;//结束时间int c;//需要的点数public Task(int s, int e, int c) {super();this.s = s;this.e = e;this.c = c;}@Overridepublic int compareTo(Task other) {int x = this.e-other.e;if(x==0) {//结束时间相等return this.s-other.s;}else {return x;}}}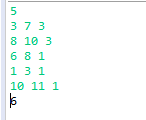
这篇关于8.4 贪心策略例题---区间选点问题的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!









