本文主要是介绍WDK李弘毅学习笔记第十周01_Unsupervised Learning: Neighbor Embedding,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
Unsupervised Learning: Neighbor Embedding
文章目录
- Unsupervised Learning: Neighbor Embedding
- 摘要
- 1、Manifold Learning
- 1.1 Locally Linear Embedding(LLE)
- 1.1.1 思想
- 1.1.2 做法
- 1.1.3 实验
- 1.2 Laplacian Eigenmaps(拉普拉斯特征映射)
- 1.2.1 思想
- 1.2.2 做法
- 1.3 T-distributed Stochastic Neighbor Embedding(T-SNE)
- 1.3.1 思想
- 1.3.2 做法
- 1.3.3 实验
- 方法
- 结论
- 展望
摘要
深度学习技术在处理实际问题时,input往往都是高维的,且有些维度对结果影响很小甚至有着负面影响,所以我们需要对数据进行降维处理,保留其影响大的维度或者建立新的维度代替原本的维度。上一章的PCA主要是对线性分布的数据进行降维,这一章将介绍如何对非线性分布的数据进行降维,常用的方法有Locally Linear Embedding(LLE)、Laplacian Eigenmaps(拉普拉斯特征映射)、T-distributed Stochastic Neighbor Embedding(T-SNE)。1、Manifold Learning
当data point是非线性分布(如下图S型分布)的时候,再用欧氏距离描述其相似性是不准确的,所以我们需要对其进行降维。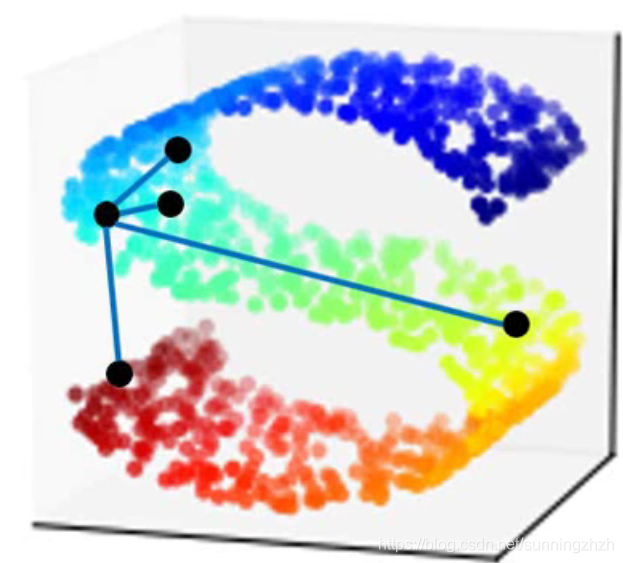
对非线性分布数据进行降维处理,变成如低维分布的数据(如下图),这就是Manifold Learning做的事情。
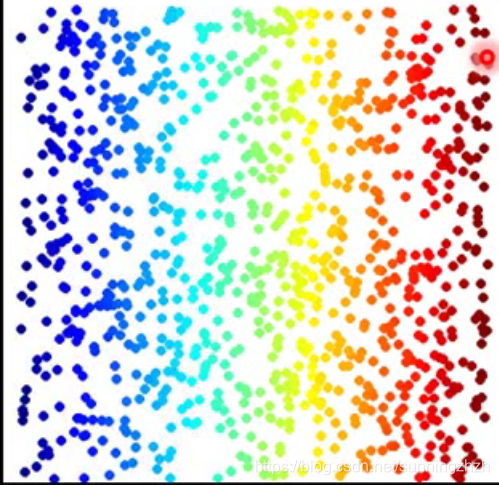
Manifold Learning常用的方法有Locally Linear Embedding(LLE)、Laplacian Eigenmaps(拉普拉斯特征映射)、T-distributed Stochastic Neighbor Embedding(T-SNE)。
1.1 Locally Linear Embedding(LLE)
1.1.1 思想
LLE是求出高维度点之间的联系,再保持其联系不变的前提下,用低纬度的点代替高纬度的点。
1.1.2 做法
- 选定一个xi,再选出k个点xj (xj是xi周围的点)。
- xj加权求和得到xi(wij是权重),wij就可以理解为xi和xj之间的联系。
- 将xi,xj转变成更低维的zi,zj,转变后的zi,zj之间的关系wij,不变。
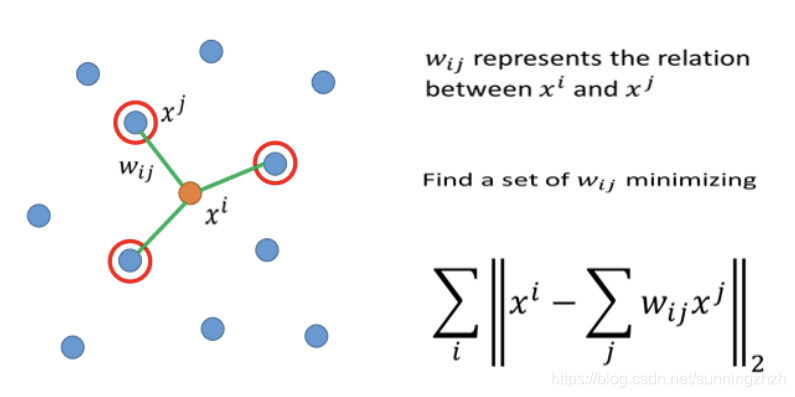
1.1.3 实验
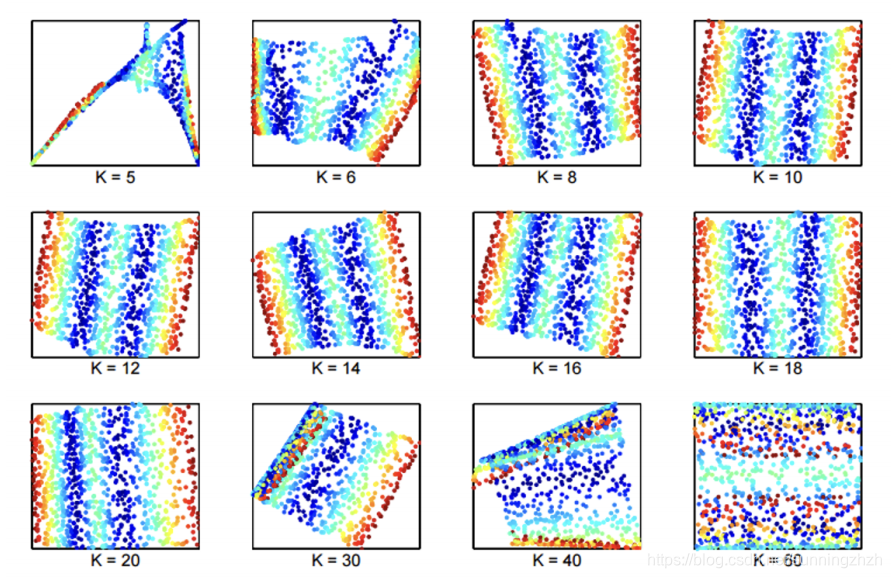
k在这个model中是一个很重要的参数,当k=5(过小)时可以发现得到的数据图像很混乱,k=60(过大)时得到的数据界限不明,所以我们需要对k进行调参选择一个合适的k值。
1.2 Laplacian Eigenmaps(拉普拉斯特征映射)
1.2.1 思想
拉普拉斯特征映射是一种基于图的降维算法,它希望相互间有关系的点在降维后的空间中尽可能的靠近,从而在降维后仍能保持原有的数据结构,也就是说如果数据xi和xj很相似,那么xi,xj在降维后的空间中应该是接近的。
1.2.2 做法
- 将所有的data point构建成图,例如可以使用KNN算法,将每个点最近的K个点连起来。
- 确定点与点之间权重Wij的大小。
- 计算拉普拉斯矩阵的特征向量与特征值,最小的m个非零特征值对应的特征向量就是降维后的data point。
1.3 T-distributed Stochastic Neighbor Embedding(T-SNE)
1.3.1 思想
T-SNE是通过求data point(xi)各个点之间的相似度,按照各个点之间的相似度将data point进行降维。
1.3.2 做法
- 计算data point各个点的相似度,相似度计算公式如下:
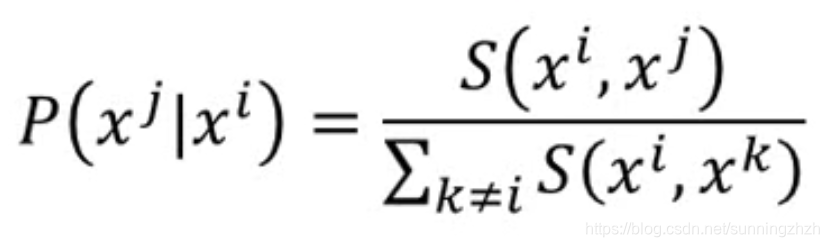
- 给降维后的点zi赋初始值,再计算zi各个点之间的相似度,计算公式如下:
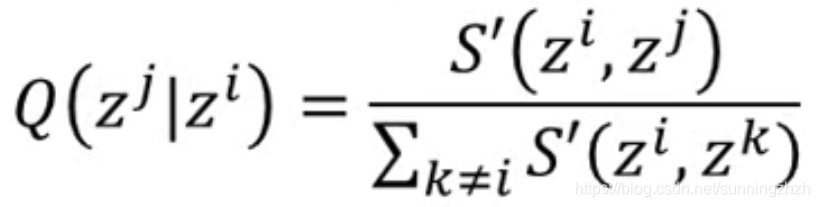
- 我们需要做的是xi,zi的分布要越接近越好,所以就用KL构建如下的Loss Function衡量xi,zi之间的相似度,用梯度下降法就可对其进行求解。
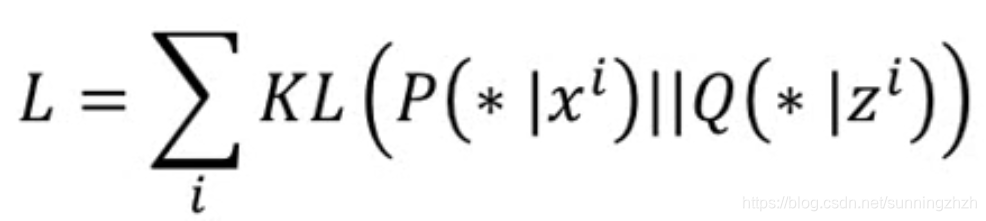
1.3.3 实验
如下图所示,我们可以发现T-SNE会放大不同类型点之间的差异,所以T-SNE适合在做完PCA或者LLE等方法降维后再对降维后的数据进行二次降维,放大数据之间的区别。
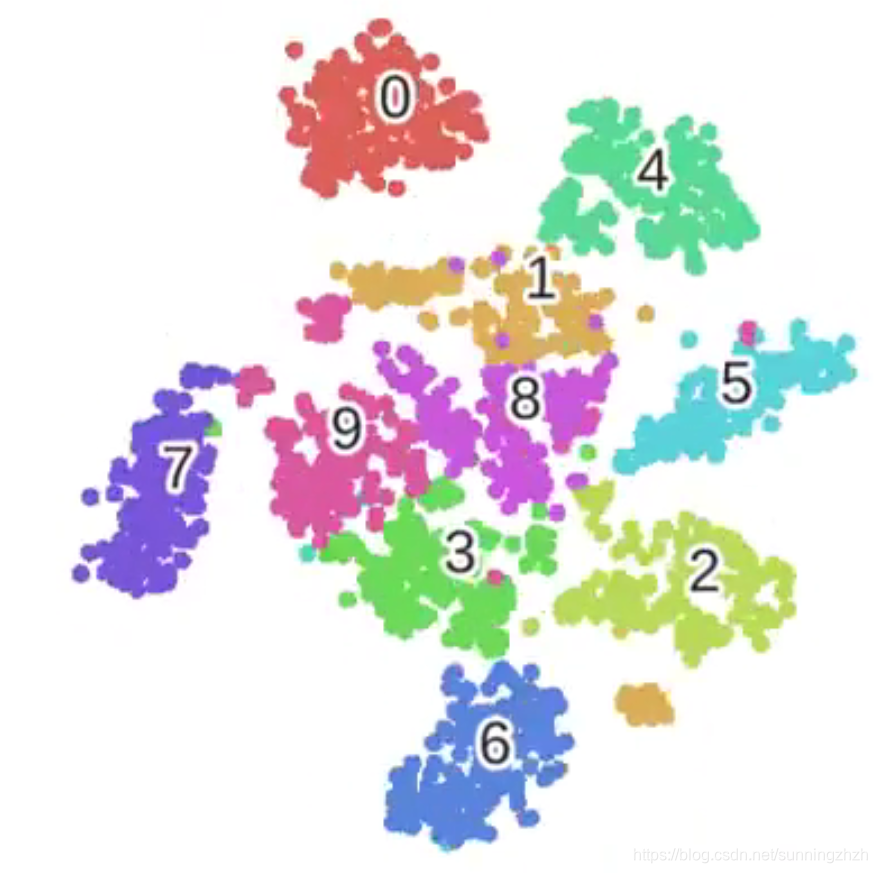
方法
以上方法的目的都是将非线性数据进行降维,不同的是降维的手段。
- LLE: 利用data point之间的联系进行降维。选定每个点和其周围点,用周围的点加权求和表示该点,这些权重就是联系,保持权重不变的情况下将全部的高维空间data point投映到低维空间。
- Laplacian Eigenmaps:将data point构建成图进行降维。将每一个点与其周围的K个点连接起来构建成图,然后定义其每个点之间权重wij的值,构建拉普拉斯矩阵,通过计算其特征向量得到其降维后的点。
- T-SNE:利用data point各个点之间的相似度进行降维。计算data point各个点之间的相似度P以及降维后的点的相似度Q,我们希望P和Q越接近越好,所以用衡量distribution相似度的函数KL得到Loss Function,对该Function用梯度下降法就可得到降维后的点。
结论
LLE、Laplacian Eigenmaps、T-SNE都可以很好的将非线性分布的数据进行降维,它们的本质都是找一组低维度的点,要求低维度点之间拥有的联系的信息和input data point之间的联系的信息尽可能相同,所以这些方法对data point分布无约束,它们不仅可以对线性分布数据进行降维也可对非线性分布数据进行降维。
展望
在实际使用中,对data point通常都需要进行多次降维处理才可以得到比较好的数据,在本章中LLE、Laplacian Eigenmaps比较适合用在第一次降维,而T-SNE因为其可以放大差异的特性,比较适合用在对降维处理过的数据进行二次降维。
这篇关于WDK李弘毅学习笔记第十周01_Unsupervised Learning: Neighbor Embedding的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






