漫漫数学之旅023

本文主要是介绍漫漫数学之旅023，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

经典格言

在我们发现的伟大事物中，“无”的存在是最伟大的。——列奥纳多·达·芬奇（Leonardo da Vinci）

嘿，大家伙儿，想象一下这个场景：列奥纳多·达·芬奇，这位文艺复兴时期的大咖，不仅是画蛋的高手（当然啦，他画的是蒙娜丽莎那种级别的），还是一位深思熟虑的思想家。有一天，他在工作室里，一手拿着画笔，另一手托着下巴，突然冒出一句：“你们知道吗？在我们追求知识、探索世界的过程中，最让人拍案惊奇的伟大发现，竟然是‘无’的存在！”

这句话要是翻译成现代幽默版，大概就像这样：“伙计们，我跟你们说，咱们研究了那么多东西，从人体构造到飞行器设计，从透视绘画到水利工程，结果万万没想到啊，最大的Boss居然是那个看似啥都没有的家伙——‘无’！就像你打开冰箱，里面除了冷气什么都没有，但那份空荡荡的感觉却实实在在告诉你，冰箱它确确实实存在。”

“无”的伟大在于它的包容性与可能性，它是空白的画布，是等待填充的乐谱，是宇宙诞生前的混沌，也是数学中零的概念，代表了起点和无限可能。达·芬奇老哥这番话虽然听起来有点玄乎，但其实就是在提醒我们：别忽略了那些看不见的东西，往往正是这些“无”，构建了我们丰富多彩的世界。所以，下回当你看到一个空房间或者一片空白的纸张时，不妨会心一笑，因为那里充满了“无”的伟大之处，正等待着你的创造力去填满它。

数学习题

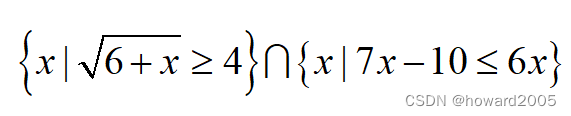
古今评注

自然数的素数“变形记”与算术基本定理的千年传奇

想象一下，你手中握着一个任意的自然数，就像一个神秘的小箱子。别看它外表平平无奇，一旦我们用一把名叫“素数分解”的神奇钥匙打开这个箱子，里面竟藏着一串独一无二、无法复制的“宝石项链”。这些“宝石”，就是构成这个自然数的素数因子。

比如，面对数字12，你可能会发现它的“宝石项链”是由两颗名为“2”的宝石和一颗名为“3”的宝石串联而成，即12=2×2×3。而不论你如何变换组合，世界上再也找不出第二个不同的素数项链能拼凑出12来。这就是数学世界中那个历经两千多年仍熠熠生辉的“算术基本定理”。

早在公元前，伟大的几何学家欧几里得在《几何原本》这部堪称古代数学百科全书的作品第4卷中，就以一种近乎魔法般的命题形式揭示了这一奥秘：“任一大于1的自然数，要么本身是素数，要么可以唯一地表示为几个素数之积。”这句话仿佛是一个古老的咒语，让每一个自然数都找到了属于自己的素数身份证，且这身份证上的信息全世界仅此一份，绝无雷同。

试想，如果每个自然数都是一个拥有独特素数身份的小小生命体，那算术基本定理就像是它们的灵魂契约，无论经历多少世纪的沧桑巨变，都无法改变其内在的本质属性。就如同童话故事中的变形记一般，无论自然数们如何“变身”，只要运用素数分解的魔力，它们的真实面目便无所遁形。

所以，当我们带着幽默风趣的眼光去审视这个看似严肃的算术基本定理时，你会发现它其实讲述了一个关于自然数们如何在素数的世界里找到自我，并保持独特个性的奇妙故事。而这则故事，不仅跨越了两千多年的时光长河，还在每一个热爱数学的人心中留下了深深的印记。

名人小传

（一）达·芬奇

达·芬奇的“跨界”人生：从文艺复兴大画家到全能型斜杠大师

让我们把时间调回到五百多年前，有个名叫列奥纳多的大叔横空出世。这位仁兄可是个不折不扣的“斜杠中年”，既是画家、雕塑家、建筑师，又是工程师、发明家、解剖学家……哦对了，他还有个响当当的名字——达·芬奇。

想象一下这样一幕：某天，达·芬奇正埋头在画布上描绘《蒙娜丽莎》那神秘微笑，突然灵感迸发：“嘿，我为何不去设计个能飞的机器呢？”于是乎，放下画笔，拿起图纸，立马变成了飞行器设计师，脑洞大开地构思起人类最早的直升机和潜水艇模型来。旁人看愣了眼，心想：“这老哥真是画得了油画，造得了飞机，还能顺手破个案（参考《达·芬奇密码》），简直是艺术与科学界的‘十项全能’选手！”

不仅如此，达·芬奇还醉心于人体解剖学的研究，他那细腻入微的解剖图，恐怕连医学院的学生都要自愧不如。每当他在实验室里挥舞着解剖刀时，邻居们可能会误以为他是要准备一道什么特别的意大利大餐，殊不知他正在探索生命的奥秘。

他的生活就像一场永不停歇的好奇探索之旅，以至于有人开玩笑说：“如果达·芬奇生在现代，大概会是TED演讲的常客，一边讲述绘画艺术的魅力，一边演示自己新研发的高科技产品。”而他自己则可能轻松回应：“我只是在用不同的方式观察这个世界罢了。”

总而言之，达·芬奇的人生就如同一部百科全书，每一页都充满了智慧与幽默，让人惊叹不已。他以一种跨越时代的创造力和全面发展的才华，成为我们今天口中那位永远的“斜杠大师”。

（二）欧几里得

欧几里得：几何世界里的幽默大师与无畏探险家

在古希腊的亚历山大港，有一位名叫欧几里得的大胡子老头儿，他并非什么街头卖艺的搞笑艺人，而是数学界的一位传奇人物。不过，如果他知道我们今天要以一种幽默风趣的方式来讲述他的故事，估计也会笑眯眯地点点头，毕竟，他用无比严谨的逻辑揭示了几何学的魅力，这本身就是一种高级的“幽默”。

欧几里得先生是个十足的理想主义者，也是个务实的教育家。他坚信“点是没有部分的”，这句话听起来像是在讲笑话——“你找不到比点更小的啦，因为它连零件都没有！”而“直线是点在同一直线上的一种无限延伸”则是他对于“没有最长，只有更长”的诙谐注解。

最令人捧腹的是他的那句名言：“给我一个支点和足够长的杠杆，我就能撬动地球。”嘿，老欧，您这是把阿基米德的豪言壮语抢过来了吧？还是您想提前预演一下物理学的力学原理呢？不管怎样，这种夸张又自信的说法，让我们看到了他敢于挑战未知、探索真理的勇气。

在他的代表作《几何原本》中，欧几里得仿佛是一位耐心的导游，带着读者们踏上了一场逻辑严密而又充满惊喜的几何之旅。每一条定理都像是一则精心设计的谜语，等待着聪明的头脑去揭开谜底。比如，那个著名的“欧几里得第五公设”（平行线公理），就像是他故意留给后世的一个顽皮玩笑，让人们琢磨了两千多年才找到答案。

总的来说，欧几里得这位古代数学家，在严肃的几何王国里插科打诨，用精准的语言和严密的逻辑构筑起了一座座知识的城堡，而那些隐藏在定理背后的幽默智慧，则成为点亮科学之路的璀璨星光。也许在他看来，能够让人在笑声中领悟几何之美，才是真正的教育艺术。

这篇关于漫漫数学之旅023的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---