TOP100 图论

本文主要是介绍TOP100 图论，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

1.200. 岛屿数量

给你一个由 '1'（陆地）和 '0'（水）组成的的二维网格，请你计算网格中岛屿的数量。

岛屿总是被水包围，并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。

此外，你可以假设该网格的四条边均被水包围。

示例 1：
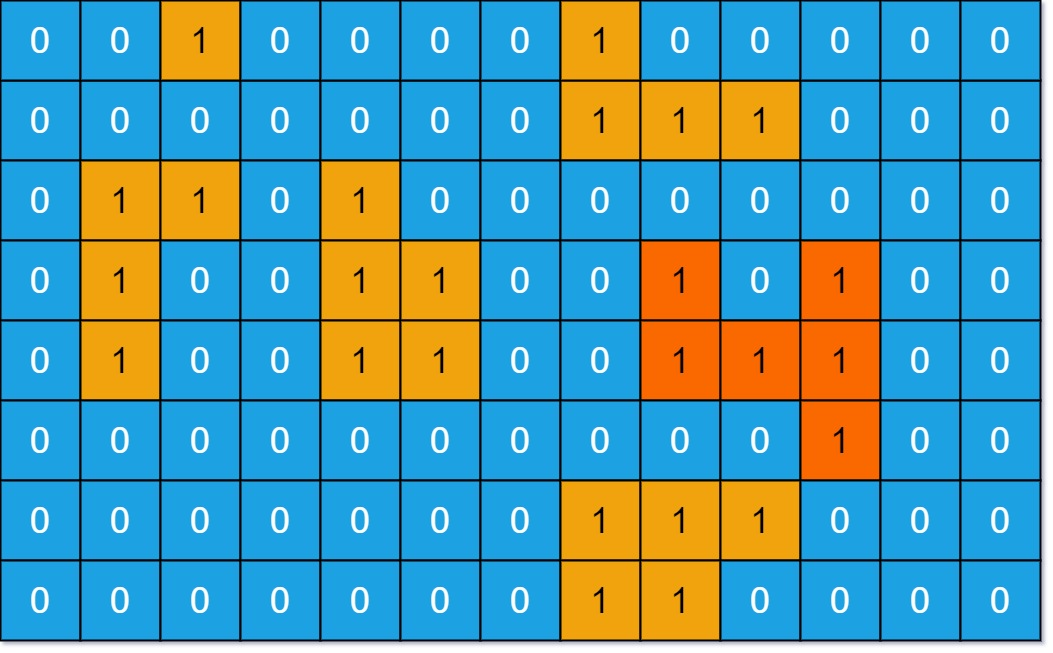
输入：grid = [["1","1","1","1","0"],["1","1","0","1","0"],["1","1","0","0","0"],["0","0","0","0","0"]
]
输出：1
示例 2：
输入：grid = [["1","1","0","0","0"],["1","1","0","0","0"],["0","0","1","0","0"],["0","0","0","1","1"]
]
输出：3
提示：

m == grid.length
n == grid[i].length
1 <= m, n <= 300
grid[i][j] 的值为 '0' 或 '1'

思路：

对于网格上的 DFS，我们完全可以参考二叉树的 DFS，写出网格 DFS 的两个要素：

首先，网格结构中的格子有多少相邻结点？答案是上下左右四个。对于格子 (r, c) 来说（r 和 c 分别代表行坐标和列坐标），四个相邻的格子分别是 (r-1, c)、(r+1, c)、(r, c-1)、(r, c+1)。换句话说，网格结构是「四叉」的。

其次，网格 DFS 中的 base case 是什么？从二叉树的 base case 对应过来，应该是网格中不需要继续遍历、grid[r][c] 会出现数组下标越界异常的格子，也就是那些超出网格范围的格子。

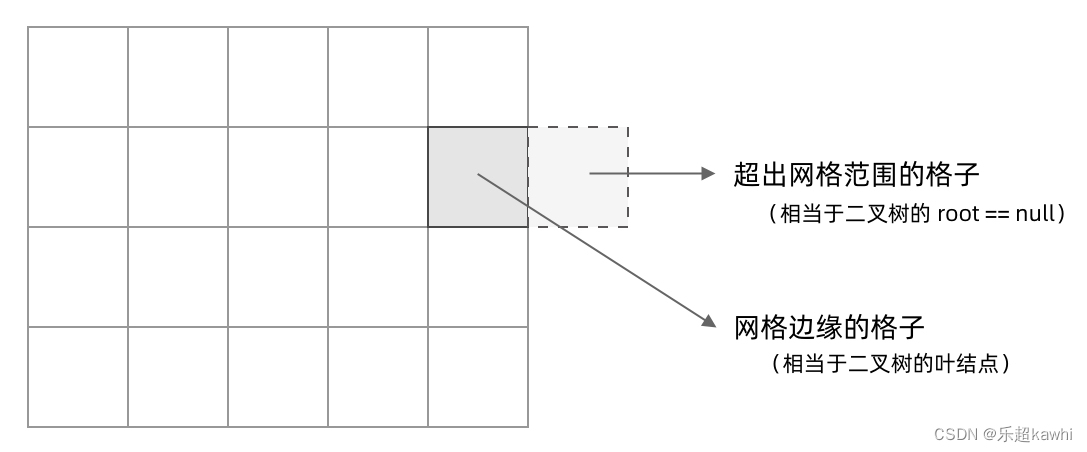
这一点稍微有些反直觉，坐标竟然可以临时超出网格的范围？这种方法我称为「先污染后治理」—— 甭管当前是在哪个格子，先往四个方向走一步再说，如果发现走出了网格范围再赶紧返回。这跟二叉树的遍历方法是一样的，先递归调用，发现 root == null 再返回。
这样，我们得到了网格 DFS 遍历的框架代码：

void dfs(int[][] grid, int r, int c) {// 判断 base case// 如果坐标 (r, c) 超出了网格范围，直接返回if (!inArea(grid, r, c)) {return;}// 访问上、下、左、右四个相邻结点dfs(grid, r - 1, c);dfs(grid, r + 1, c);dfs(grid, r, c - 1);dfs(grid, r, c + 1);
}// 判断坐标 (r, c) 是否在网格中
boolean inArea(int[][] grid, int r, int c) {return 0 <= r && r < grid.length && 0 <= c && c < grid[0].length;
}

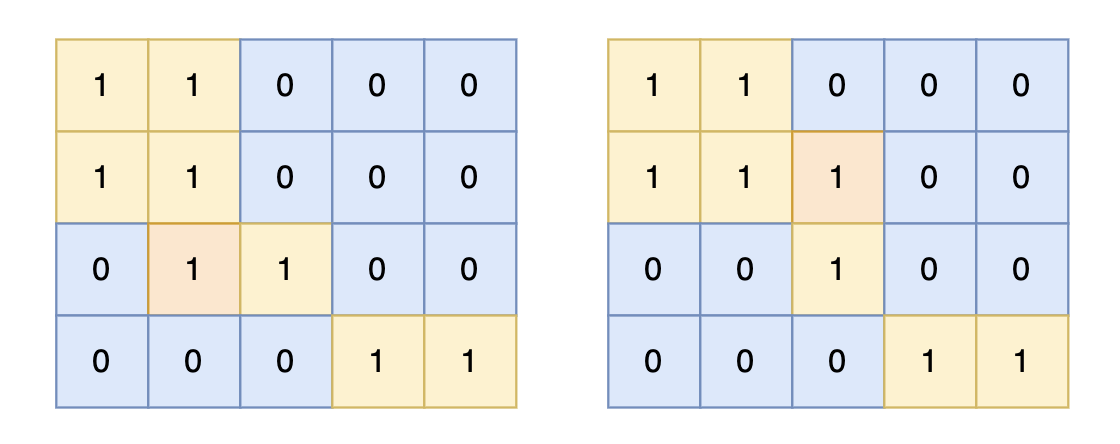
网格结构的 DFS 与二叉树的 DFS 最大的不同之处在于，遍历中可能遇到遍历过的结点。这是因为，网格结构本质上是一个「图」，我们可以把每个格子看成图中的结点，每个结点有向上下左右的四条边。在图中遍历时，自然可能遇到重复遍历结点。

这时候，DFS 可能会不停地「兜圈子」，永远停不下来，如下图所示：

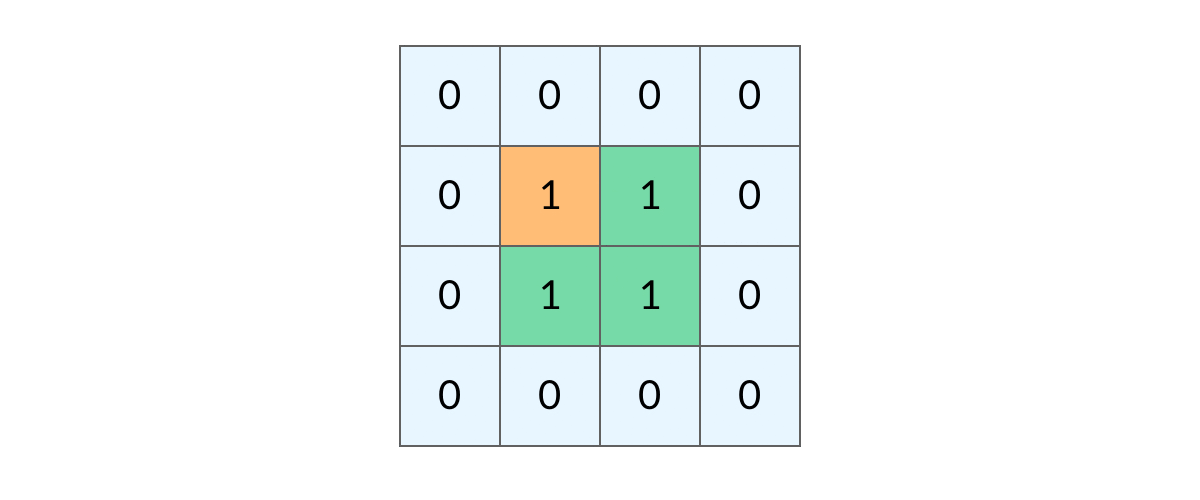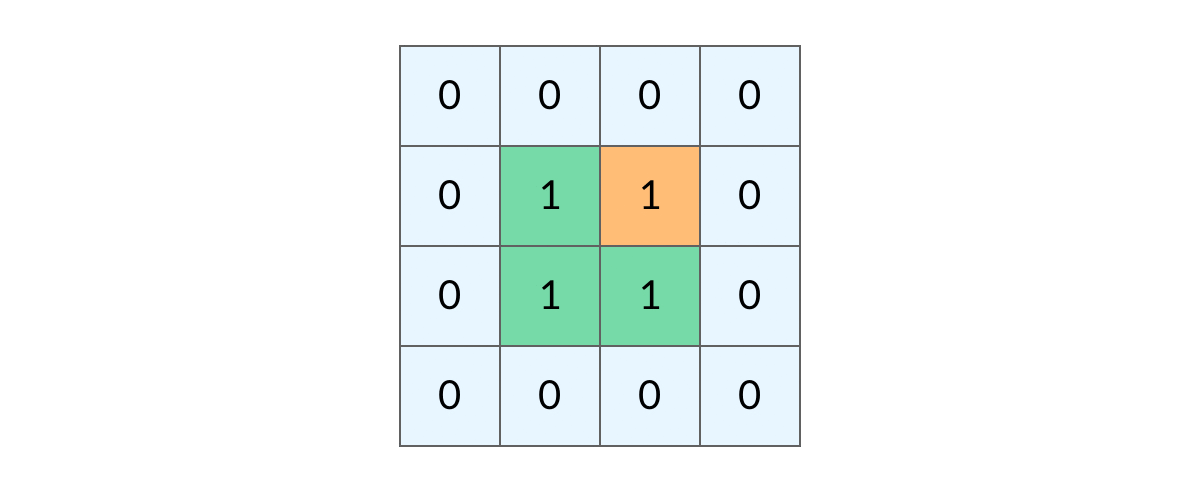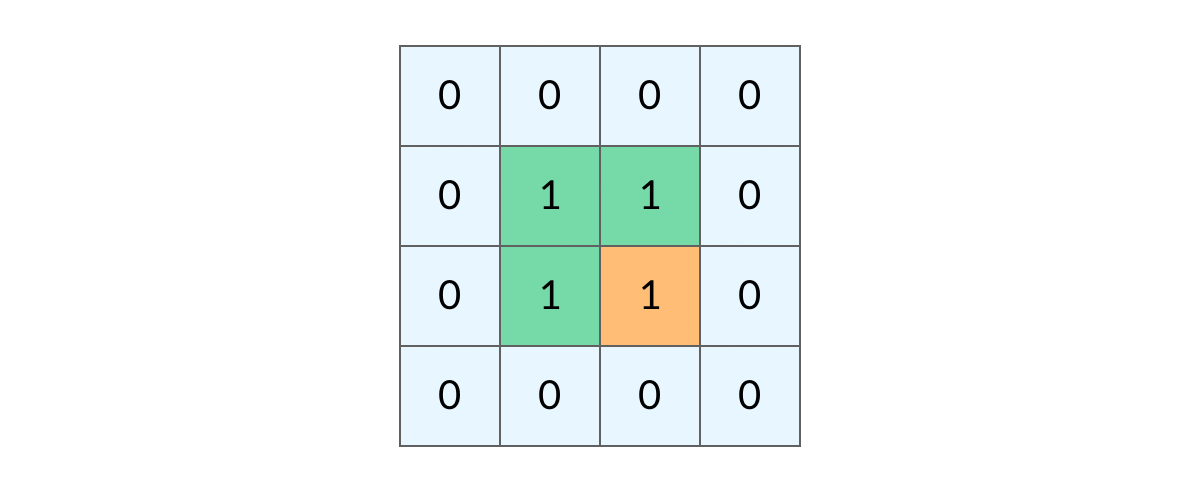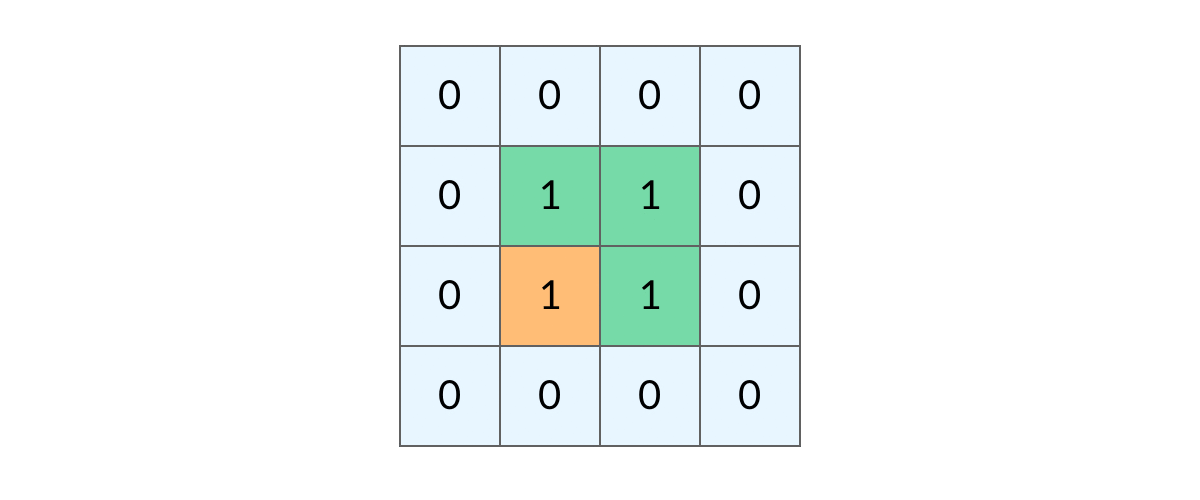
如何避免这样的重复遍历呢？答案是标记已经遍历过的格子。以岛屿问题为例，我们需要在所有值为 1 的陆地格子上做 DFS 遍历。每走过一个陆地格子，就把格子的值改为 2，这样当我们遇到 2 的时候，就知道这是遍历过的格子了。也就是说，每个格子可能取三个值：

0 —— 海洋格子
1 —— 陆地格子（未遍历过）
2 —— 陆地格子（已遍历过）
我们在框架代码中加入避免重复遍历的语句：

void dfs(int[][] grid, int r, int c) {// 判断 base caseif (!inArea(grid, r, c)) {return;}// 如果这个格子不是岛屿，直接返回if (grid[r][c] != 1) {return;}grid[r][c] = 2; // 将格子标记为「已遍历过」// 访问上、下、左、右四个相邻结点dfs(grid, r - 1, c);dfs(grid, r + 1, c);dfs(grid, r, c - 1);dfs(grid, r, c + 1);
}// 判断坐标 (r, c) 是否在网格中
boolean inArea(int[][] grid, int r, int c) {return 0 <= r && r < grid.length && 0 <= c && c < grid[0].length;
}

代码：

class Solution {//利用深度递归解决，可以看图，并加记住这个模板，他可以解决岛屿中的问题，还有一题岛屿面积问题也是这个模板。public int numIslands(char[][] grid) {//定义一个表示岛屿数量的变量int count = 0;//这个两层for循环是用来遍历整张二维表格中所有的陆地//其中 i 表示行，j 表示列for(int i = 0; i<grid.length;i++){for(int j =0;j<grid[0].length;j++){//取出所有的陆地if(grid[i][j] == '1'){//深度递归，遍历所有的陆地dfs(grid,i,j);//用来统计有多少岛屿，岛屿是由多个陆地组成的，概念不一样count++;}}}//返回岛屿的数量return count;}public void dfs(char[][] grid,int i, int j){//防止 i 和 j 越界，也就是防止超出岛屿（上下左右）的范围。特别注意当遍历到海洋的时候也退出循环if(i<0||j<0||i>=grid.length||j>=grid[0].length||grid[i][j]=='0') return;//将遍历过的陆地改为海洋，防止重复遍历grid[i][j]='0';//上，dfs(grid,i+1,j);//下dfs(grid,i-1,j);//右dfs(grid,i,j+1);//左dfs(grid,i,j-1);}
}

2.695. 岛屿的最大面积

给你一个大小为 m x n 的二进制矩阵 grid 。

岛屿是由一些相邻的 1 (代表土地) 构成的组合，这里的「相邻」要求两个 1 必须在 水平或者竖直的四个方向上 相邻。你可以假设 grid 的四个边缘都被 0（代表水）包围着。

岛屿的面积是岛上值为 1 的单元格的数目。

计算并返回 grid 中最大的岛屿面积。如果没有岛屿，则返回面积为 0 。

示例 1：

输入：grid = [[0,0,1,0,0,0,0,1,0,0,0,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,1,1,0,1,0,0,0,0,0,0,0,0],[0,1,0,0,1,1,0,0,1,0,1,0,0],[0,1,0,0,1,1,0,0,1,1,1,0,0],[0,0,0,0,0,0,0,0,0,0,1,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,0,0,0,0,0,0,1,1,0,0,0,0]]
输出：6
解释：答案不应该是 11，因为岛屿只能包含水平或垂直这四个方向上的 1。

示例 2：

输入：grid = [[0,0,0,0,0,0,0,0]]
输出：0

提示：

m == grid.length
n == grid[i].length
1 <= m, n <= 50
grid[i][j] 为 0 或 1

思路：

这道题目只需要对每个岛屿做 DFS 遍历，求出每个岛屿的面积就可以了。求岛屿面积的方法也很简单，代码如下，每遍历到一个格子，就把面积加一：

int area(int[][]grid,int r, int c){if (!inArea(grid, r, c)) {return 0;}if (grid[r][c] != 1) {return 0;}grid[r][c] = 2;return 1+area(grid,r-1,c)+area(grid,r+1,c)+area(grid,r,c-1)+area(grid,r,c+1);
}

代码：

class Solution{public int maxAreaOfIsland(int[][] grid) {int res = 0;for (int r = 0; r < grid.length; r++) {for (int c = 0; c < grid[0].length; c++) {if (grid[r][c] == 1) {int a = area(grid, r, c);res = Math.max(res, a);}}}return res;
}int area(int[][] grid, int r, int c) {if (!inArea(grid, r, c)) {return 0;}if (grid[r][c] != 1) {return 0;}grid[r][c] = 2;return 1 + area(grid, r - 1, c)+ area(grid, r + 1, c)+ area(grid, r, c - 1)+ area(grid, r, c + 1);
}boolean inArea(int[][] grid, int r, int c) {return 0 <= r && r < grid.length && 0 <= c && c < grid[0].length;}
}

3.827. 最大人工岛

这个蛮难的

给你一个大小为 n x n 二进制矩阵 grid 。最多只能将一格 0 变成 1 。

返回执行此操作后，grid 中最大的岛屿面积是多少？

岛屿由一组上、下、左、右四个方向相连的 1 形成。

示例 1:

输入: grid = [[1, 0], [0, 1]]
输出: 3
解释: 将一格0变成1，最终连通两个小岛得到面积为 3 的岛屿。

示例 2:

输入: grid = [[1, 1], [1, 0]]
输出: 4
解释: 将一格0变成1，岛屿的面积扩大为 4。

示例 3:

输入: grid = [[1, 1], [1, 1]]
输出: 4
解释: 没有0可以让我们变成1，面积依然为 4。

提示：

n == grid.length
n == grid[i].length
1 <= n <= 500
grid[i][j] 为 0 或 1

思路：

大致的思路我们不难想到，我们先计算出所有岛屿的面积，在所有的格子上标记出岛屿的面积。然后搜索哪个海洋格子相邻的两个岛屿面积最大。

力扣（LeetCode）官网 - 全球极客挚爱的技术成长平台

代码：

class Solution {public int largestIsland(int[][] grid) {if (grid == null || grid.length == 0) return 1;int result = 0, index = 2;HashMap<Integer, Integer> areasMap = new HashMap();for (int i = 0; i < grid.length; i++)for (int j = 0; j < grid[0].length; j++)if (grid[i][j] == 1) areasMap.put(index, calculateAreas(index++, grid, i, j)); // 只计算未编号的岛屿if (areasMap.size() == 0) return 1; // 没有岛屿，全是海洋for (int i = 0; i < grid.length; i++) {for (int j = 0; j < grid[0].length; j++) {if (grid[i][j] == 0) {Set<Integer> islands = getIslands(grid, i, j);if (islands.size() == 0) continue; // 周围没有岛屿result = Math.max(result, islands.stream().map(item -> areasMap.get(item)).reduce(Integer::sum).orElse(0) + 1);}}}if (result == 0) return areasMap.get(2); // 全是岛屿，没有海洋return result;}public int calculateAreas(int index, int[][] grid, int row, int column) {if (!isLegal(grid, row, column) || grid[row][column] != 1) return 0;grid[row][column] = index;return calculateAreas(index, grid, row + 1, column) + calculateAreas(index, grid, row - 1, column) + calculateAreas(index, grid, row, column - 1) + calculateAreas(index, grid, row, column + 1) + 1;}public boolean isLegal(int[][] grid, int row, int column) {return row >= 0 && row < grid.length && column >= 0 && column < grid[0].length;}public Set<Integer> getIslands(int[][] grid, int row, int column) {Set<Integer> result = new HashSet<>();if (isLegal(grid, row + 1, column) && grid[row + 1][column] != 0)result.add(grid[row + 1][column]);if (isLegal(grid, row - 1, column) && grid[row - 1][column] != 0)result.add(grid[row - 1][column]);if (isLegal(grid, row, column - 1) && grid[row][column - 1] != 0)result.add(grid[row][column - 1]);if (isLegal(grid, row, column + 1) && grid[row][column + 1] != 0)result.add(grid[row][column + 1]);return result;}
}

4.994. 腐烂的橘子

在给定的 m x n 网格 grid 中，每个单元格可以有以下三个值之一：

值 0 代表空单元格；
值 1 代表新鲜橘子；
值 2 代表腐烂的橘子。

每分钟，腐烂的橘子 周围 4 个方向上相邻 的新鲜橘子都会腐烂。

返回 直到单元格中没有新鲜橘子为止所必须经过的最小分钟数。如果不可能，返回 -1 。

示例 1：

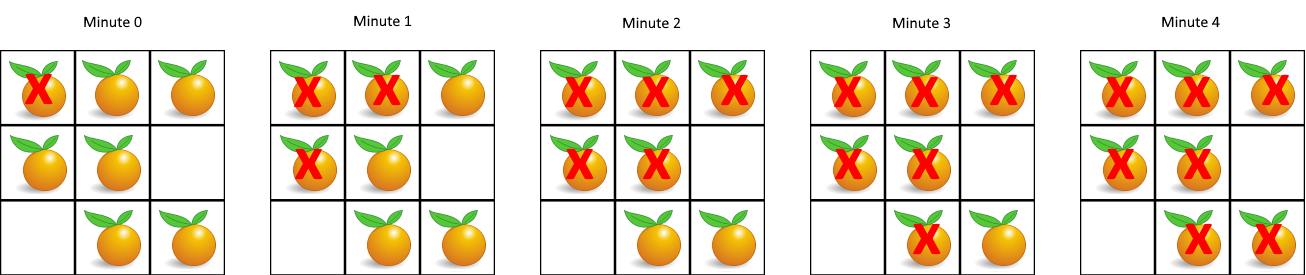
输入：grid = [[2,1,1],[1,1,0],[0,1,1]]
输出：4

示例 2：

输入：grid = [[2,1,1],[0,1,1],[1,0,1]]
输出：-1
解释：左下角的橘子（第 2 行， 第 0 列）永远不会腐烂，因为腐烂只会发生在 4 个方向上。

示例 3：

输入：grid = [[0,2]]
输出：0
解释：因为 0 分钟时已经没有新鲜橘子了，所以答案就是 0 。

提示：

m == grid.length
n == grid[i].length
1 <= m, n <= 10
grid[i][j] 仅为 0、1 或 2

思路：

这道题的主要思路是：

一开始，我们找出所有腐烂的橘子，将它们放入队列，作为第 0 层的结点。
然后进行 BFS 遍历，每个结点的相邻结点可能是上、下、左、右四个方向的结点，注意判断结点位于网格边界的特殊情况。
由于可能存在无法被污染的橘子，我们需要记录新鲜橘子的数量。在 BFS 中，每遍历到一个橘子（污染了一个橘子），就将新鲜橘子的数量减一。如果 BFS 结束后这个数量仍未减为零，说明存在无法被污染的橘子。

代码：

class Solution {public int orangesRotting(int[][] grid) {int M=grid.length;int N=grid[0].length;Queue<int []> queue =new LinkedList<>();int count=0;//新鲜橘子的数量for (int r = 0; r < M; r++) {for (int c = 0; c < N; c++) {if (grid[r][c] == 1) {count++;} else if (grid[r][c] == 2) {queue.add(new int[]{r, c});}}}int round = 0; // round 表示腐烂的轮数，或者分钟数while (count > 0 && !queue.isEmpty()) {round++;int n = queue.size();for (int i = 0; i < n; i++) {int[] orange = queue.poll();int r = orange[0];int c = orange[1];if (r-1 >= 0 && grid[r-1][c] == 1) {grid[r-1][c] = 2;count--;queue.add(new int[]{r-1, c});}if (r+1 < M && grid[r+1][c] == 1) {grid[r+1][c] = 2;count--;queue.add(new int[]{r+1, c});}if (c-1 >= 0 && grid[r][c-1] == 1) {grid[r][c-1] = 2;count--;queue.add(new int[]{r, c-1});}if (c+1 < N && grid[r][c+1] == 1) {grid[r][c+1] = 2;count--;queue.add(new int[]{r, c+1});}}}if (count > 0) {return -1;} else {return round;}}
}

这篇关于TOP100 图论的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！